Ultimate Related Rates Study Guide (cars approaching an intersection, water into a tank, $ more)
TLDRThis comprehensive study guide delves into related rates in calculus, covering various scenarios from a circular metal plate's area expansion to the rising water level in a conical tank. The guide also tackles the changing distance between two ships, the rate at which two cars approach each other, and the increasing angle of a balloon ascending vertically. Each problem is meticulously explained with diagrams and mathematical formulas, illustrating how to apply related rates concepts to real-world situations. The guide encourages practice and understanding of the material for mastery of calculus-related rates problems.
Takeaways
- 📚 The study guide covers advanced calculus topics related to rates, suitable for various math classes including College Calculus 1, AP Calculus AB, and GCSE Calculus.
- 🥳 Practice is emphasized as essential for mastering difficult calculus problems, with a link provided in the description for additional questions.
- 📈 The concept of related rates is introduced through the example of a heated circular metal plate, where both radius and area change over time.
- 🌀 The rate of change of the circle's radius (dr/dt) and area (da/dt) are related, with the formula for the area of a circle used to find the rate of change of the area.
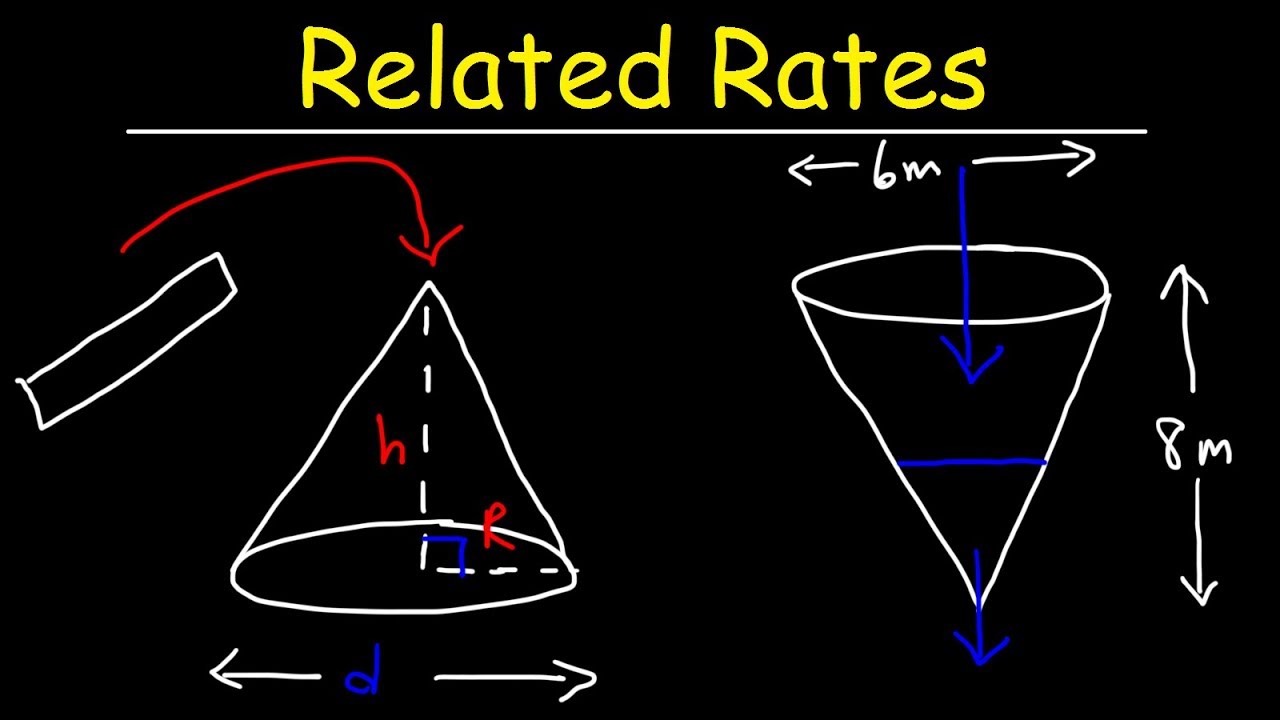
- 🏢 A water tank problem is presented, involving an inverted cone filled with water at a constant rate, aiming to find the rate at which the water level rises.
- 📊 The volume of a cone formula is used to relate the rate of water flow to the change in water level height in the tank.
- 🏗️ A ladder against a wall problem illustrates the use of related rates to find the speed at which the top of the ladder slides down the wall as the bottom moves away.
- 🚗 Car A and B approach an intersection from perpendicular directions, and the related rates are used to determine their rate of approaching each other.
- 🛳️ The distance change between two ships is calculated using related rates, with one ship traveling south and the other north.
- 📐 The area of a triangle with a changing angle is found by using the formula involving the sides' lengths and the sine of the angle.
- 🎈 The angle of inclination of an observer's line-of-sight to a rising balloon is determined using related rates, with the balloon's height changing at a constant rate.
- 🔢 The importance of understanding the relationships between changing quantities and constants is stressed, as well as the need to pay attention to the units of measurement and the direction of change.
Q & A
What is the main topic of the video?
-The main topic of the video is related rates in calculus, specifically focusing on how different quantities change with respect to time in various scenarios.
How does the video introduce the concept of related rates?
-The video introduces related rates by discussing how two quantities, such as the radius and area of a circle, change with respect to time when a circular metal plate is heated.
What is the formula for the area of a circle?
-The formula for the area of a circle is A = πr², where A is the area and r is the radius of the circle.
How does the video explain the relationship between the rate of change of the radius and the rate of change of the area of a circle?
-The video explains that by differentiating the area formula with respect to time, we can find the relationship between the rate of change of the radius (dr/dt) and the rate of change of the area (da/dt). It uses the chain rule and the derivative to establish this relationship.
What is the rate at which the radius of the circular metal plate increases?
-The radius of the circular metal plate increases at a rate of 0.02 centimeters per minute.
How does the video approach the problem of a water tank being filled?
-The video approaches the problem by first visualizing the water tank as an inverted circular cone. It then uses the given dimensions of the tank and the rate at which water is being pumped in to find the rate at which the water level is rising.
What is the volume formula for a cone?
-The volume formula for a cone is V = (1/3)πr²h, where V is the volume, r is the radius of the base, and h is the height of the cone.
How does the video solve for the rate at which the water level is rising in the tank?
-The video solves for the rate at which the water level is rising by using the volume formula for a cone, differentiating it with respect to time, and plugging in the given values to find dH/dt, the rate of change of the height of the water.
What is the initial height of the water in the tank when it is being pumped in at a rate of two cubic meters per minute?
-The initial height of the water in the tank is three meters when it is being pumped in at a rate of two cubic meters per minute.
How does the video illustrate the concept of similar triangles in the context of the water tank problem?
-The video illustrates the concept of similar triangles by showing that the triangle formed by the water level and the original base radius of the tank are similar. This is used to derive a relationship between the radius and height of the water cone, allowing for the elimination of one variable and simplifying the problem.
Outlines
📚 Calculus: Related Rates - Circular Metal Plate
This paragraph introduces a calculus problem involving a circular metal plate whose radius increases at a rate of 0.02 cm/min. The goal is to determine the rate at which the area of the plate is increasing when the radius is 60 cm. The explanation involves using the formula for the area of a circle (A = πr^2), taking the derivative with respect to time, and plugging in the given values to find the rate of change of the area (dA/dt). The problem is solved by applying the chain rule of differentiation and understanding the relationship between the radius and the area of a circle as functions of time.
💧 Calculus: Related Rates - Water Tank Filling
The second paragraph discusses a related rates problem concerning a water tank shaped like an inverted circular cone. Given the base radius and height of the tank, and the rate at which water is pumped in, the task is to find the rate at which the water level is rising when the water depth is three meters. The solution involves understanding the volume formula for a cone (V = 1/3πr^2h), setting up an equation based on the given dimensions and rate of water flow, and differentiating this equation with respect to time to find the rate of change of the water level (dh/dt). The explanation also includes the use of similar triangles to relate the changing dimensions of the water-filled cone.
📈 Calculus: Related Rates - Cone Volume and Similar Triangles
This paragraph continues the discussion on the related rates problem involving a cone-shaped water container. The focus is on differentiating the volume formula of the cone with respect to time and using the properties of similar triangles to simplify the equation. The explanation involves identifying the changing variables (radius and height of the water cone), setting up the volume equation, and applying the chain rule for differentiation. The solution requires algebraic manipulation to isolate the rate of change of the water level and understanding how the dimensions of the cone change as water is added.
📐 Calculus: Related Rates - Ladder Against a Wall
The fourth paragraph presents a related rates problem involving a ladder leaning against a wall. The challenge is to determine how fast the top of the ladder is sliding down the wall when the bottom of the ladder moves away at a rate of one foot per second, and the bottom is two feet away from the wall. The solution involves creating a right triangle model, applying the Pythagorean theorem, and differentiating the equation with respect to time to find the rate of change of the vertical distance (dy/dt). The explanation emphasizes understanding the relationship between the changing horizontal and vertical distances and the constant length of the ladder.
🚗 Calculus: Related Rates - Cars Approaching Intersection
This paragraph describes a related rates problem involving two cars moving towards an intersection. Car A is traveling west and Car B is traveling north, and the task is to find the rate at which the cars are approaching each other when Car A is 0.3 miles and Car B is 0.4 miles away from the intersection. The solution involves setting up a right triangle model based on the cars' positions and speeds, applying the Pythagorean theorem, and differentiating the equation with respect to time to find the rate of change of the distance between the cars (dC/dt). The explanation highlights the need to consider the direction of the cars' movement when determining the rate of change.
🚢 Calculus: Related Rates - Ships Moving Apart
The sixth paragraph discusses a related rates problem involving two ships moving apart from each other. Ship A is moving west and Ship B is moving north, and the goal is to find the rate at which the distance between the ships is changing at 4 o'clock, given their initial positions and speeds. The explanation involves creating a right triangle model, applying the Pythagorean theorem, and differentiating the equation with respect to time to find the rate of change of the distance (dC/dt). The solution requires calculating the distances traveled by each ship and understanding how these distances change over time.
🔺 Calculus: Related Rates - Triangle Area and Angle
The ninth paragraph presents a related rates problem involving a triangle with two sides of fixed length and an angle between them that is increasing at a rate of 0.06 radians per second. The task is to find the rate at which the area of the triangle is increasing when the angle is π/3 radians. The solution involves using the formula for the area of a triangle (A = 1/2 * sides * sin(angle)), differentiating this formula with respect to time, and plugging in the given values to find the rate of change of the area (dA/dt). The explanation emphasizes understanding how the area of a triangle changes as the angle between its sides increases.
🎈 Calculus: Related Rates - Balloon Ascending
The eleventh paragraph describes a related rates problem involving an observer on the ground watching a balloon ascending vertically. The balloon is initially 500 feet away from the observer, and the task is to find the rate at which the angle of inclination of the observer's line of sight is increasing at the instant when the balloon is 400 feet above the observer's eyes. The solution involves setting up a right triangle with the observer's line of sight, applying the tangent function, and differentiating the equation with respect to time to find the rate of change of the angle (dθ/dt). The explanation highlights the relationship between the changing height of the balloon and the angle of inclination as functions of time.
Mindmap
Keywords
💡Calculus
💡Related Rates
💡Derivative
💡Radius
💡Area
💡Water Level
💡Conical Tank
💡Rate of Change
💡Chain Rule
💡Pythagorean Theorem
💡Trigonometry
Highlights
The study guide covers a variety of calculus-related rates problems suitable for different levels of calculus classes.
A circular metal plate's radius increases at a rate of 0.02 centimeters per minute, and the guide explains how to determine the rate of area increase.
The area of a circle is used as a basis for the calculations, with the formula A = πr^2.
Differentiation with respect to time is a key method used to find rates of change in the study guide.
The guide provides a clear demonstration of how to set up and solve related rate problems through step-by-step examples.
A water tank problem is used to illustrate how to find the rate of water level rise in a conical tank being filled.
The volume of a cone is derived using the formula V = (1/3)πr^2h, which is crucial for solving the water tank problem.
The guide explains the use of similar triangles to solve for unknown variables in geometry-related rate problems.
A ladder against a wall problem is used to demonstrate how to find the rate of change in one variable based on the rate of another.
The Pythagorean theorem is applied to relate the changing distances in the ladder problem.
Two cars approaching an intersection from perpendicular directions is a problem that illustrates the concept of relative velocity.
The study guide shows how to use the Pythagorean theorem and differentiation to find the rate at which the cars are approaching each other.
A problem involving two ships moving away from each other at different speeds demonstrates how to calculate the rate of change of distance between them.
The guide uses the Pythagorean theorem and the concept of differentiation to solve for the rate of change in the distance between the ships.
A triangle's area is related to the sides and the included angle, with the formula A = (1/2)ab*sin(θ).
The study guide explains how to find the rate of increase of a triangle's area when the angle between two fixed sides is increasing.
A hot air balloon ascending problem is used to illustrate how to find the rate of change of the angle of inclination of an observer's line-of-sight.
The use of tangent and differentiation is demonstrated to find the rate of change of the angle in the hot air balloon problem.
Transcripts
Browse More Related Video

Related Rates - Distance Problems - Application of Derivatives

Step by Step Method of Solving Related Rates Problems - Conical Example
Related Rates - Conical Tank, Ladder Angle & Shadow Problem, Circle & Sphere - Calculus

Related Rates

Calculus AB Homework 4.2: Related Rates
Related Rates - Gravel Dumped Into Conical Tank Problem
5.0 / 5 (0 votes)
Thanks for rating: