Step by Step Method of Solving Related Rates Problems - Conical Example
TLDRIn this educational video, the presenter tackles a challenging related rates problem from calculus, involving the filling of a conical water tank. The step-by-step explanation guides viewers through identifying the variables, using the volume formula for a cone, and applying related rates to find the rate of water level rise when the tank is partially filled. The solution is clear, methodical, and engaging, ultimately demonstrating the practical application of calculus concepts.
Takeaways
- 📚 The topic is related rates in calculus, which can be tricky and commonly challenges students.
- 💡 The problem involves an inverted cone water tank with given dimensions and water being pumped in at a specified rate.
- 🔍 The goal is to find the rate at which the water level is rising when the water depth is 3 meters.
- 📈 To solve the problem, it's crucial to understand the concept of derivatives and rates of change in calculus.
- 📊 The script outlines a step-by-step approach to tackle the problem, emphasizing not to panic despite the complexity.
- 🗂️ Key variables include the rate of water inflow (2 m³/minute), the tank's dimensions (radius of 2m, height of 4m), and the water depth (3m).
- 🔑 The volume of the cone is given by the formula V = (1/3)πR²H, which is essential for solving the problem.
- 📐 The concept of similar triangles is used to eliminate the radius variable, simplifying the equation to focus on the height (H).
- 🌀 The derivative dV/dt is taken to find the rate of change of volume with respect to time, leading to the expression for dH/dt.
- 📝 By plugging in the values and solving the derived equation, the rate of water level rise is found to be 8/9π when the water is 3 meters deep.
- 🎓 The video encourages understanding the meaning of derivatives and following a methodical approach to solve related rate problems.
Q & A
What is the main topic of the video?
-The main topic of the video is solving a related rates problem in calculus, specifically focusing on the rate at which the water level is rising in an inverted cone-shaped tank.
What are the dimensions of the water tank mentioned in the problem?
-The water tank is an inverted cone with a radius of 2 meters and a height of 4 meters.
At what rate is water being pumped into the cone?
-Water is being pumped into the cone at a rate of 2 meters cubed per minute.
What is the depth of the water for which we need to find the rising rate?
-We need to find the rate at which the water level is rising when the water is 3 meters deep.
How does the video suggest approaching related rates problems?
-The video suggests not panicking, identifying what is being looked for, understanding the variables, and using the knowledge of calculus and rates of change to solve the problem.
What is the volume formula for a cone?
-The volume formula for a cone is V = (1/3)πr^2h, where r is the radius and h is the height.
How are similar triangles used in this problem?
-Similar triangles are used to eliminate the variable R (radius of the water level) by creating a proportion based on the similar triangles formed by the height of the water and the height of the cone.
What is the simplified volume formula for the water in the tank?
-The simplified volume formula for the water in the tank is V = (π/12)H^3, where H is the height of the water.
How is the derivative of volume with respect to time represented?
-The derivative of volume with respect to time is represented as dV/dt, which is the rate of change of the volume of water over time.
What is the final expression for the rate of change of the water level with respect to time?
-The final expression for the rate of change of the water level with respect to time is dH/dt = (8/9)π.
What is the rate at which the water level is rising when the water is 3 meters deep?
-When the water is 3 meters deep, the water level is rising at a rate of 0.28 meters per minute.
Outlines
📚 Introduction to Related Rates in Calculus
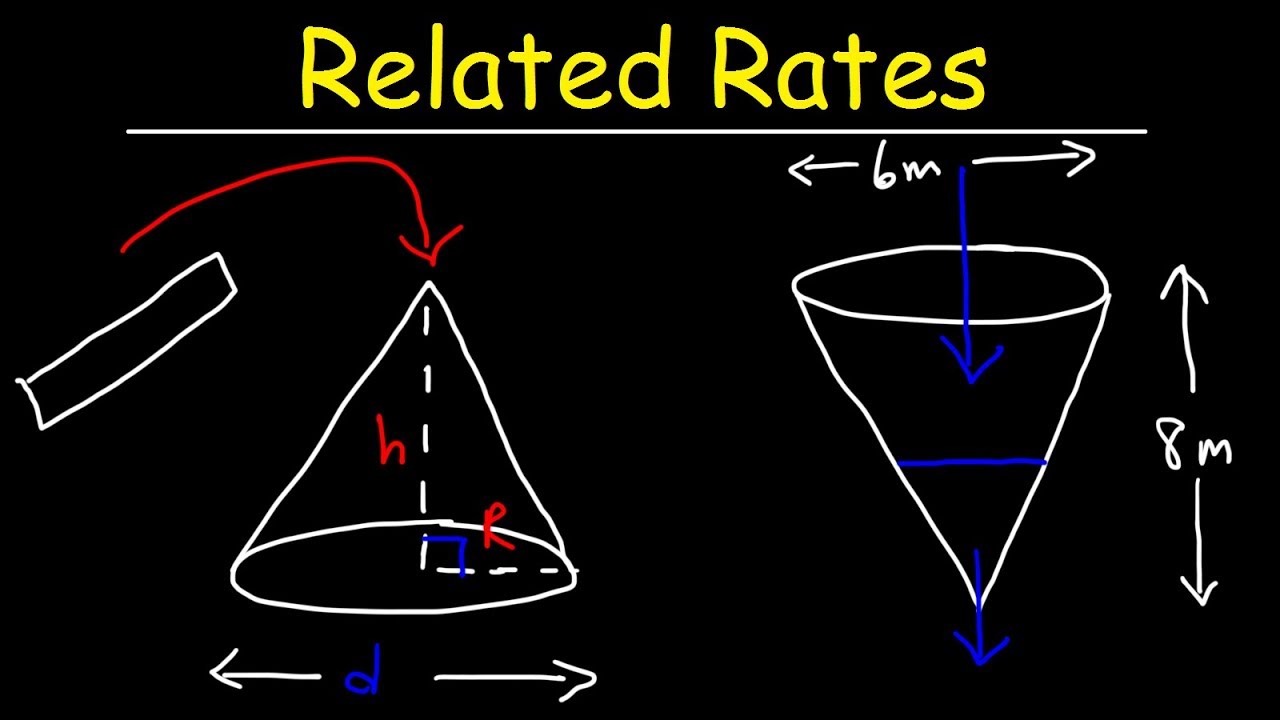
The video begins with the host, Fred, introducing the topic of related rates in calculus. He emphasizes the complexity and common struggle students face with this subject. Fred outlines the goal of the video, which is to work through a specific problem involving a water tank in the shape of an inverted cone. The tank has a radius of 2 meters and a height of 4 meters, and water is being pumped into it at a rate of 2 cubic meters per minute. The problem is to find the rate at which the water level is rising when the water is 3 meters deep. Fred encourages viewers not to panic despite the presence of multiple variables and assures that understanding the question is the first step towards solving it. He introduces the concept of using calculus to measure rates of change in real-life scenarios, highlighting the practical application of the subject.
🧠 Solving the Cone Water Tank Problem
In this paragraph, Fred dives deeper into solving the water tank problem. He explains the need to eliminate variables and focuses on the volume of the cone, which is given by the formula 1/3 πR^2H. By using the properties of similar triangles, Fred establishes a relationship between the radius and the height of the water (R = H/2). He then substitutes this relationship into the volume formula, simplifying it to a function of H only. Fred proceeds to take the derivative of the volume with respect to time (dV/dt), which leads to an expression involving dH/dt - the rate of change of the water height that the problem seeks to find. By isolating dH/dt, Fred sets up the equation to solve for the rate at which the water level is rising. He then plugs in the given values (H = 3 meters and dV/dt = 2 cubic meters per minute) to find that the water level rises at a rate of 8/9π meters per minute, or approximately 0.28 meters per minute. Fred concludes by reiterating the importance of understanding the concept of derivatives and following a systematic approach to solving related rate problems.
Mindmap
Keywords
💡Related Rates
💡Inverted Cone
💡Derivatives
💡Volume
💡Similar Triangles
💡Implicit Differentiation
💡Volume of a Cone
💡Rate of Change
💡Calculus
💡Water Level Rise
Highlights
The topic of discussion is related rates, a challenging subject in calculus with real-world applications.
The problem involves an inverted cone water tank with a radius of 2 meters and a height of 4 meters being filled with water.
Water is being pumped into the tank at a rate of 2 cubic meters per minute.
The goal is to find the rate at which the water level is rising when the water is 3 meters deep.
The approach involves using calculus to understand rates of change and apply them to real-life scenarios.
The volume of water in the tank changes with respect to time, given as 2 cubic meters per minute.
The volume of a cone is given by the formula 1/3 * pi * R^2 * H, where R is the radius and H is the height.
By using similar triangles, the relationship between the radius of the water level and the height of the water is established as R = H/2.
The volume formula is simplified to V = (pi/12) * H^3 by substituting the relationship between R and H.
The derivative of the volume with respect to time (dV/dt) is taken to find the rate of change of the water level.
Implicit differentiation is used to solve for the rate of change of the water level (dH/dt).
The derivative is used to create an equation to solve for dH/dt, the rate at which the water level is rising.
When the water is 3 meters deep, the rate of rise of the water level is found to be 8/9 * pi.
The final answer is that the water rises at a rate of approximately 0.28 meters per minute when 3 meters deep.
Understanding the concept of derivatives is crucial for solving related rate problems.
The method involves identifying what is given and what is needed, and following a systematic approach to solve the problem.
The use of similar triangles to eliminate variables is a key technique in solving related rate problems involving geometric shapes.
Memorizing the formulas for the volumes of basic shapes like cones, cylinders, and spheres is essential for tackling related rate problems.
Transcripts
Browse More Related Video

Related Rates Cone Example (Calculus)

Related Rates - Filling a Cone Problem

Related Rate Problem #3 - Volume of a Conical Tank
Lec 13 | MIT 18.01 Single Variable Calculus, Fall 2007

Ultimate Related Rates Study Guide (cars approaching an intersection, water into a tank, $ more)
Related Rates - Gravel Dumped Into Conical Tank Problem
5.0 / 5 (0 votes)
Thanks for rating: