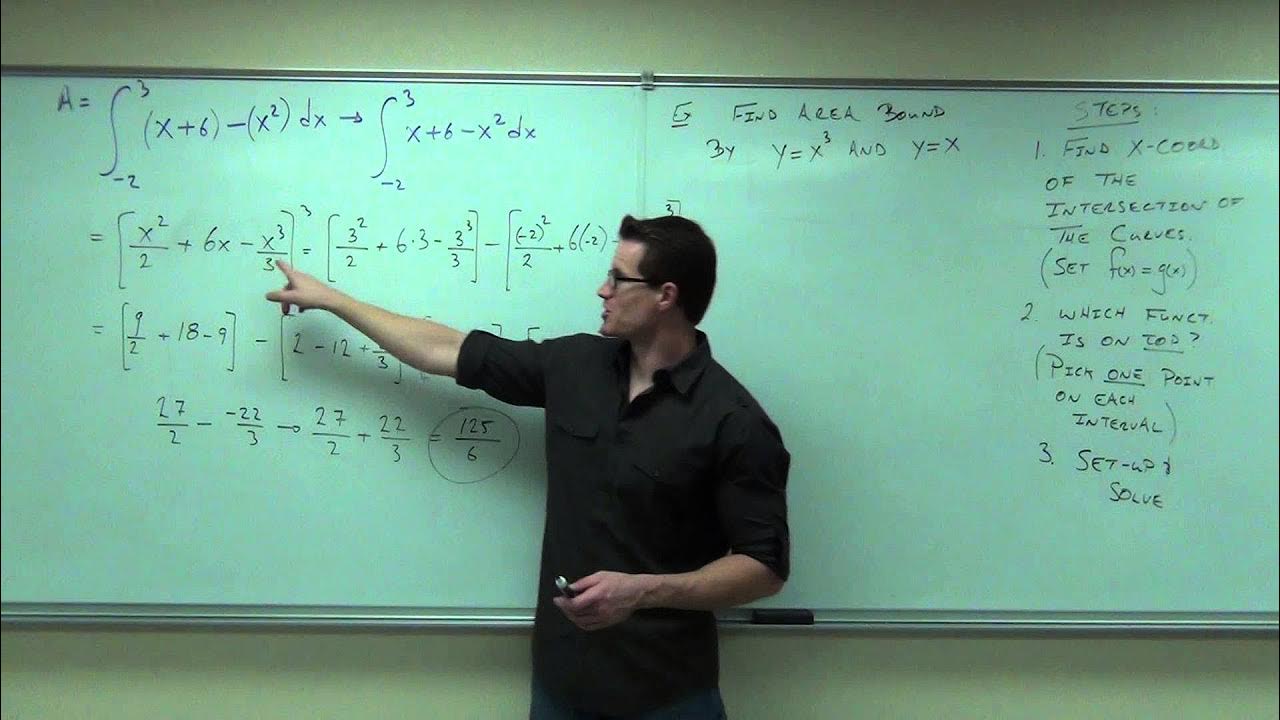Calculus Rhapsody

WordGospel09
22 May 200906:04
EducationalLearning
32 Likes 10 Comments

TLDRThe transcript appears to be a casual and informal discussion about various concepts in calculus, including continuity, limits, derivatives, and integrals. The speaker seems to be reflecting on their learning experience and the application of these mathematical concepts, such as finding areas under curves and differentiating equations. The conversation takes a light-hearted turn with the mention of 'dance' and 'whipped cream,' suggesting an attempt to make the complex subject matter more enjoyable. The speaker concludes by expressing satisfaction with their comprehensive review of the topic.

Takeaways
  • 📚 The script discusses various concepts in calculus, including continuity, limits, derivatives, and integrals.
  • 🎶 There is a humorous mention of singing about calculus topics, indicating a lighthearted approach to learning.
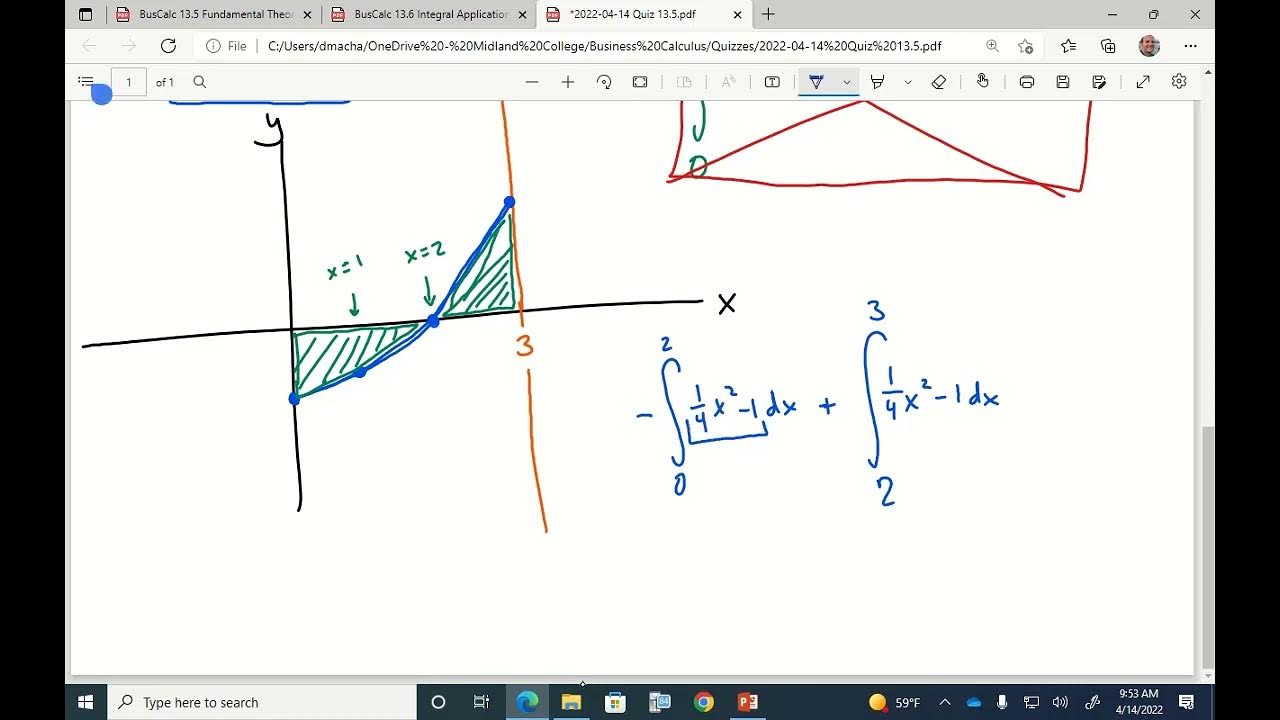
  • 🤔 The concept of finding areas between curves is mentioned, which relates to integration.
  • 💃 A dance metaphor is used to remember the process of finding areas under curves, emphasizing the importance of the integration process.
  • 🚫 The script touches on the idea that forgetting steps (or processes) can lead to incorrect results.
  • 🌟 The mention of 'x equals' suggests the beginning of an equation or problem-solving approach.
  • 🍰 A whimsical reference to whipped cream on the y-axis highlights the creative ways to visualize mathematical concepts.
  • 🏆 The concept of limits and infinity is briefly introduced, likely in the context of limit processes.
  • 📈 The script implies that understanding differentiability is crucial for working with equations in calculus.
  • 🛤️ There is an expression of satisfaction with the phrase 'that was fun yeah,' indicating an enjoyable learning experience.
  • 🎓 The final statement 'oh' suggests a sense of accomplishment or realization that the entire topic has been covered.
Q & A

  • What does it mean when the script asks if a function 'f' is continuous?

    -In mathematics, asking if a function 'f' is continuous means checking whether there are any breaks, jumps, or points of discontinuity in its graph. A function is continuous at a point if the limit at that point equals the function's value there.

  • How is the limit process used to determine continuity?

    -The limit process helps determine continuity by calculating the function's limit as it approaches a certain point from both directions. If these limits are equal and match the function's value at that point, the function is continuous there.

  • Why does the script mention no sharp points or asymptotes in relation to a function?

    -Mentioning no sharp points or asymptotes suggests characteristics of a smooth curve, indicative of a continuous and differentiable function. Sharp points could imply corners or cusps, and asymptotes suggest behavior where the function heads towards infinity, both complicating continuity and differentiability.

  • What are derivatives and integrals as referred to in the script?

    -Derivatives represent the rate of change of a function, useful for understanding slopes and tangents on graphs. Integrals, on the other hand, represent the accumulation of values, useful for calculating areas under curves, among other things.

  • How can you find the area between two curves?

    -The area between two curves can be calculated by integrating the difference of their respective functions over a given interval. The integral of the top function minus the bottom function over the interval gives the enclosed area.

  • What does it imply when the script discusses 'multiplying by the change' in a mathematical context?

    -Multiplying by the change likely refers to calculating differential quantities in calculus, such as using small increments or decrements (deltas) in variables to approximate changes in function values, integral sums, or in derivative calculations.

  • What is meant by 'integration' and how is it related to 'area under curve'?

    -Integration is a fundamental concept in calculus used to compute the area under a curve. By integrating a function over a specified interval, you sum up infinitesimally small areas to find the total area between the curve and the x-axis.

  • How does the script link the concepts of limits, infinity, and differentiation?

    -The script connects these concepts as fundamental tools in calculus. Limits involve approaching a point or infinity in function evaluation, differentiation relates to calculating derivatives or rates of change, and both are critical for analyzing function behaviors at boundaries and infinities.

  • Why does the script personify mathematical concepts like 'nobody loves me' for y-axis?

    -This personification adds a humorous or memorable touch to the learning material, making abstract concepts more relatable and easier to remember. It creatively engages students by humanizing the y-axis, often used in integration and as a reference in plots.

  • What is the significance of saying 'any mere equation, it is differentiable, for me'?

    -This phrase highlights the notion that many basic equations in calculus are differentiable, meaning their derivatives exist. This simplifies many calculus problems and is a cornerstone for understanding changes and rates within those equations.

Outlines
00:00
📚 Introduction to Calculus Concepts

This paragraph delves into the foundational concepts of calculus, touching upon continuity, limits, derivatives, and integrals. The speaker expresses a sense of accomplishment and familiarity with these mathematical ideas, indicating a solid understanding of the subject matter. The paragraph begins with a casual inquiry about the nature of a function being discussed, transitioning into a more structured exploration of calculus techniques. The mention of finding areas between curves and the equation 'x equals' suggests an application of integral calculus, specifically the use of the fundamental theorem of calculus to calculate definite integrals. The paragraph concludes with a playful reference to a 'dance', possibly indicating a mnemonic or ritual associated with problem-solving in calculus.

05:16
🎶 The Joy of Understanding Differentiation

The second paragraph takes on a more reflective and appreciative tone, as the speaker acknowledges the beauty and challenge of differentiable equations. The paragraph conveys a sense of satisfaction and accomplishment in mastering the craft of calculus, with a particular focus on differentiation. The speaker's enthusiasm is evident, as they express that the session was enjoyable and that they believe they have covered the entire topic comprehensively. The paragraph ends on a light-hearted note, suggesting a positive and engaging learning experience.

Mindmap
Keywords
💡calculus
Calculus is a branch of mathematics that deals with rates of change and accumulation. It is foundational to the study of functions and their properties, particularly in relation to derivatives and integrals. In the script, calculus is mentioned as a subject where one can learn about finding derivatives and integrals, which are key concepts in understanding the behavior of mathematical functions and their applications.
💡continuous function
A continuous function is one where there are no gaps, jumps, or breaks in the graph. In other words, you can draw the function's graph without lifting the pen from the paper. The script implies that the function being discussed, 'f', is continuous, suggesting that it has no sharp points or asymptotes, which means it is well-behaved and its graph can be drawn in one continuous line.
💡limit process
The limit process is a fundamental concept in calculus that helps in understanding the behavior of functions as their input values approach a particular point. It is used to define the derivative of a function at a certain point and to calculate the area under a curve. In the context of the script, the limit process is likely being used to analyze the function 'f' and to perform calculations related to it.
💡differentiation
Differentiation is the mathematical process of finding the derivative of a function, which represents the rate of change or the slope of the function at any given point. It is a crucial tool in calculus for analyzing the behavior of functions, including their maxima, minima, and points of inflection. The script mentions differentiation as one of the many things learned in calculus, indicating its importance in understanding the function 'f'.
💡integrals
Integrals are a fundamental concept in calculus that represent the accumulation of a quantity over an interval. They are used to calculate the area under a curve, the displacement of an object, and other quantities that involve summing small changes. In the script, the speaker mentions finding the area between two curves using integrals, which is a practical application of this concept.
💡area under a curve
The area under a curve refers to the region enclosed by the graph of a function and the x-axis over a certain interval. This area can be calculated using integration, which is a key technique in calculus. The script mentions finding this area, which is often used in various real-world applications, such as determining the total distance traveled by an object or the accumulated effect of a variable over time.
💡asymptotes
Asymptotes are lines that a function's graph approaches but never actually intersects, no matter how far along the x-axis or y-axis you go. They are used to describe the behavior of a function at its limits. The script mentions that the function 'f' does not have asymptotes, indicating that its graph does not approach any such lines, which is a characteristic of certain types of functions, like polynomials.
💡change
In the context of the script, 'change' likely refers to the process of transformation or alteration in the value of a function's input or output. It is a fundamental concept in calculus, as the study of rates of change is at the core of both differentiation and integration. The script mentions 'the change' in relation to finding areas under curves, which could be referring to the variable increments used in the process of integration.
💡y-axis
The y-axis is one of the two primary坐标轴 (coordinate axes) in the Cartesian coordinate system, with the other being the x-axis. It is a vertical line that intersects the x-axis at the origin (the point 0,0) and extends infinitely in both directions. In the script, the y-axis is mentioned in a metaphorical context, 'nobody loves me, y-axis with whipped cream,' which could be a playful way to express the importance or the challenge of working with the y-axis in calculus problems.
💡equation
An equation is a mathematical statement that asserts the equality of two expressions. It often involves unknowns, which are typically represented by variables. In the context of the script, equations are likely used to represent functions and their relationships, which are essential in calculus for finding derivatives, integrals, and analyzing the behavior of functions.
💡differentiable
A function is said to be differentiable at a point if it has a derivative at that point, meaning the rate of change of the function is well-defined and finite. Differentiability is an important property in calculus because it allows for the application of differentiation rules and the study of a function's local behavior. The script suggests that the function 'f' is differentiable, which implies it has a well-defined derivative and its graph does not have any sharp corners or cusps.
Highlights

Discussion on the concept of continuity in functions and its importance in calculus.

Mention of the limit process as a fundamental tool in calculus for understanding functions' behavior.

Identification of functions without sharp points or asymptotes as being continuous.

Reference to the vast knowledge in calculus, including various techniques and concepts.

The application of calculus in finding derivatives, which is crucial for analyzing functions' rates of change.

Integration as a method to calculate areas between curves, providing practical applications in various fields.

The importance of the area under a curve, which can be found using integration.

The use of the 'dance' as a metaphor for the process of solving calculus problems, emphasizing the need for a methodical approach.

The concept of change as a central theme in calculus, particularly in the context of finding derivatives.

The mention of 'whipped cream' as a metaphor for the y-axis, illustrating the application of calculus in a fun and engaging way.

The idea of finding limits as a key aspect of understanding the behavior of functions at their extremes.

Differentiation as a powerful tool for analyzing and solving equations.

The notion that any mere equation can be differentiable, showcasing the versatility of calculus.

The overall enjoyment and satisfaction derived from engaging with calculus and its concepts.

The sense of accomplishment from completing a comprehensive exploration of calculus topics.

Transcripts

Browse More Related Video

Learn to Solve an Integral (What Makes You Beautiful Parody) AP Calculus BC

BusCalc 13.6 Integral Applications

Calculus 1 Lecture 5.1: Finding Area Between Two Curves

Differentiation | Class 11 | JEE | PACE SERIES

Limits 01 | Introduction | CLASS 11 | JEE | PACE SERIES

Музыка из Псковского порно 1 час

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Mathematics FunCalculus ConceptsEducational TunesDance TutorialLimit ProcessesDerivative SecretsIntegral MysteriesCreative LearningMath and MusicEngaging Content