Differentiation | Class 11 | JEE | PACE SERIES

Physics Wallah - Alakh Pandey

26 Feb 202146:38

EducationalLearning

32 Likes 10 Comments

TLDRThe transcript appears to be a lecture on derivatives, covering basic concepts and mathematical principles related to differentiation. It introduces the topic, discusses the importance of understanding derivatives in functions, and explores various rules such as the product rule and quotient rule. The speaker uses examples and analogies to explain complex concepts, aiming to clarify the process of finding derivatives and their applications in mathematics.

Takeaways

📚 The session focuses on derivatives, also known as differentiation, and is part of a series on the basics of derivatives.
👨‍🏫 The instructor introduces the concept of derivatives, explaining that they represent the slope of a curve at a particular point, akin to the steepness of a candidate standing on a table.
📈 Derivatives are discussed in the context of functions and their graphical representation, emphasizing the importance of understanding the slope of the tangent to a curve at any given point.
🔍 The lecture delves into the mathematical process of finding derivatives, including the use of limits and the first principle method to calculate derivatives with respect to a variable.
📝 The importance of memorizing formulas and rules for differentiation is highlighted, as they are fundamental to solving problems in calculus.
📚 The transcript mentions various chapters and parts of the course, indicating a structured curriculum covering different aspects of derivatives, such as the second part of the derivatives chapter and the method of depression.
🧮 The application of derivatives in real-world scenarios, such as finance and research analysis, is briefly touched upon, showing the practical relevance of the concept.
📉 The process of finding the derivative of a function is exemplified with mathematical expressions and the use of specific formulas, illustrating the step-by-step approach to differentiation.
🤔 The transcript includes rhetorical questions and prompts for audience engagement, suggesting an interactive teaching style aimed at clarifying concepts and ensuring understanding.
🔧 The use of specific mathematical terms in both English and a code-switching language (Hindi/Urdu) indicates a bilingual approach to teaching, possibly catering to a diverse audience.
📚 The session concludes with an emphasis on the importance of practice and the application of learned concepts, encouraging students to apply their knowledge to solve problems.

Q & A

What is the main topic of the lecture in the script?
-The main topic of the lecture is derivatives, specifically focusing on the basics of differentiation and its application in various contexts.
What is the significance of the slope in the context of derivatives mentioned in the script?
-In the context of derivatives, the slope represents the rate of change of a function at a particular point, which is a fundamental concept in calculus.
What does the term 'first principle method' refer to in the script?
-The 'first principle method' in the script refers to a basic approach to finding derivatives, which involves the concept of limits and the rate of change of a function.
What is the purpose of discussing the 'first principle method' in the lecture?
-The purpose of discussing the 'first principle method' is to provide a clear understanding of how derivatives are calculated from the most basic level, which is essential for grasping more complex derivative concepts.
What is the relationship between derivatives and the slope of a function's graph as mentioned in the script?
-The relationship between derivatives and the slope of a function's graph is that the derivative of a function at a point equals the slope of the tangent line to the graph of the function at that point.
How does the script describe the process of finding the derivative of a function?
-The script describes the process of finding the derivative of a function by using the first principle method, which involves taking the limit of the difference quotient as it approaches zero.
What is the importance of understanding the basic formulas of derivatives as highlighted in the script?
-Understanding the basic formulas of derivatives is important because they provide a foundation for solving more complex problems and are essential tools in various fields such as physics, engineering, and economics.
What is the role of the 'difference quotient' in the script's explanation of derivatives?
-The 'difference quotient' plays a crucial role in the script's explanation of derivatives as it is the formula used to calculate the rate of change between two points on a function, which leads to the derivative at a specific point.
How does the script connect the concept of derivatives to real-world applications?
-The script connects the concept of derivatives to real-world applications by mentioning different fields such as market research, financial analysis, and scientific research, where the understanding of rates of change is crucial.
What is the meaning of the term 'tangent' in the context of the script?
-In the context of the script, 'tangent' refers to a straight line that touches the curve of a function at a single point, and its slope at that point is equal to the derivative of the function.

Outlines

00:00

📚 Introduction to Derivatives and Differentiation

The speaker begins by addressing the audience, presumably students, and introduces the topic of derivatives and differentiation. They mention that the session will focus on specific aspects of differentiation, including the basics of derivatives. The speaker also refers to a 'second part' which might involve more advanced concepts such as the method of depression, possibly a term related to market analysis or a specific mathematical method. The paragraph ends with the speaker expressing hope that everyone is ready to start the journey of learning about derivatives and their applications.

05:00

📈 Derivative Concepts and Line Slope

This paragraph delves into the concept of derivatives as the slope of a line. The speaker uses the analogy of a car's speed and the slope of a straight line to explain derivatives. They discuss the formula for calculating the slope, which involves the difference in y-coordinates (Δy) and the difference in x-coordinates (Δx). The explanation includes a step-by-step breakdown of the formula and its components, emphasizing the importance of understanding the basic principles of derivatives.

10:03

🔍 Detailed Explanation of Derivatives and the Delta Method

The speaker provides a detailed explanation of derivatives, mentioning different methods such as the delta method, also known as the ABC method or the ABCD method. They discuss the process of determining derivatives, using the first principle method and the concept of limited approaches. The paragraph includes a complex formula and a step-by-step guide to finding the derivative of a function with respect to x, using the first principle method. The speaker also touches on the topic of finance, possibly relating derivatives to financial concepts.

15:16

🎓 Advanced Derivative Concepts and First Principle Method

The speaker continues to elaborate on advanced concepts of derivatives, focusing on the first principle method. They discuss the process of finding derivatives with respect to elders, a term that might be used to denote a specific variable or concept in the context. The explanation involves complex mathematical expressions and the use of scientific formulas. The speaker also mentions the importance of understanding the underlying principles of derivatives and their applications in various fields.

20:18

📘 Derivative Formulas and Mathematical Functions

This paragraph focuses on the formulas and functions related to derivatives. The speaker mentions various functions and their derivatives, including the derivative of a square function with respect to x. They use the first principle method to derive the formulas and explain the process of finding the derivative of a function. The speaker also emphasizes the importance of understanding the basic differentiation formulas and their applications in solving mathematical problems.

25:21

📚 Summary of Derivative Rules and Theorems

The speaker summarizes various rules and theorems related to derivatives. They discuss the product rule, the quotient rule, and the chain rule, which are fundamental in differentiation. The explanation includes how to apply these rules to different functions and the importance of remembering these theorems for solving problems involving derivatives. The speaker also mentions the need to practice and understand these concepts thoroughly.

30:22

🧑‍🏫 Final Thoughts on Derivatives and Learning

In the final paragraph, the speaker wraps up the discussion on derivatives. They mention the importance of learning and understanding the concepts of derivatives, as well as the rules and theorems associated with them. The speaker encourages the audience to practice and apply the knowledge they have gained throughout the session. They end on a positive note, expressing hope that everyone has enjoyed the learning experience and is ready to continue their journey in understanding derivatives.

Mindmap

Keywords

💡Derivatives

Derivatives in the context of this video refer to the mathematical concept of a derivative, which is a measure of how a function changes as its input changes. It is a fundamental concept in calculus and is central to the video's theme of discussing differentiation. The script mentions 'derivatives' multiple times, indicating its importance in understanding the rate at which a function's value changes.

💡Differentiation

Differentiation is the process of finding the derivative of a function. It is a key operation in calculus and is used to analyze the behavior of functions. The video script discusses 'differentiation' in the context of mathematical functions, emphasizing its role in determining the slope of a function's graph, which is a critical aspect of the video's educational content.

💡Slope

Slope is a concept in mathematics that refers to the steepness or gradient of a line. In the video, 'slope' is used to describe the tangent of the angle a line makes with the x-axis, which is derived from the derivative of the function. The script mentions 'slope' in the context of explaining how derivatives can be used to find the slope of a curve at any point, illustrating a practical application of derivatives.

💡First Principles

First Principles is a methodological approach that involves breaking down complex problems into their most fundamental elements. In the script, 'First Principles' is used to describe a method for finding derivatives, emphasizing a basic understanding of the concept rather than relying on memorized formulas. It is presented as a way to derive new formulas from scratch, which is a key teaching point in the video.

💡Limit

In mathematics, a 'limit' is the value that a function or sequence 'approaches' as the input or index approaches some value. The concept of 'limit' is crucial in understanding derivatives, as it is used to define the derivative in terms of the limit of a difference quotient. The video script refers to 'limit' in the context of explaining the process of finding derivatives using the First Principles method.

💡Function

A 'function' in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. The video script frequently mentions 'function' in the context of differentiation, discussing how to find the derivative of various functions, which is essential for understanding changes in the function's behavior.

💡Graph

A 'graph' in the context of mathematics is a visual representation of the relationship between two or more variables, often used to plot the behavior of functions. The script discusses 'graph' in relation to functions and their derivatives, explaining how the derivative can be visualized as the slope of the tangent line on the graph of the function.

💡Tangent

A 'tangent' line in mathematics touches a curve at a single point without crossing it. In the video, 'tangent' is used to describe the line that has the same slope as the curve at a particular point, which is found using the derivative. The script explains the concept of a tangent in the context of differentiation, showing its relevance in understanding the local behavior of functions.

💡Chain Rule

The 'Chain Rule' is a fundamental theorem in calculus for finding the derivative of a composite function. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. The script refers to the 'Chain Rule' as part of the process of differentiating more complex functions, which is a crucial concept for advanced differentiation techniques.

💡Product Rule

The 'Product Rule' is a calculus theorem that allows for the differentiation of a product of two functions. It states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. The video script mentions the 'Product Rule' in the context of differentiating functions that are products of other functions, which is an important technique in calculus.

Highlights

Introduction to derivatives and differentiation, focusing on the basics of specific differentiation.

Explaining the concept of derivatives as the slope of a curve at a particular point.

Differentiation methods, including the first principle method and its application in finance.

The importance of understanding the basic functions and their derivatives in calculus.

Discussion on the derivative of a function as the limit approaching zero.

The use of the first principle method to find derivatives with respect to elders in finance.

Illustration of how to calculate the derivative using the slope of a line between two points.

Explanation of the tangent line and its slope in relation to the derivative of a function.

Differentiation of basic mathematical functions like sine, cosine, and their inverses.

The concept of increasing and decreasing functions and their derivatives.

Application of derivatives in optimization problems and finding maximum or minimum values.

Differentiation rules such as the product rule, quotient rule, and chain rule.

The use of derivatives in physics for concepts like velocity and acceleration.

Integration of derivatives in economics for modeling supply and demand curves.

Practical examples of derivatives in stock markets and financial instruments.

The impact of derivatives on risk management and decision-making in businesses.

Summary of the essential differentiation formulas and their applications.

Concluding remarks on the importance of derivatives in various fields and future learning.

Transcripts

Browse More Related Video

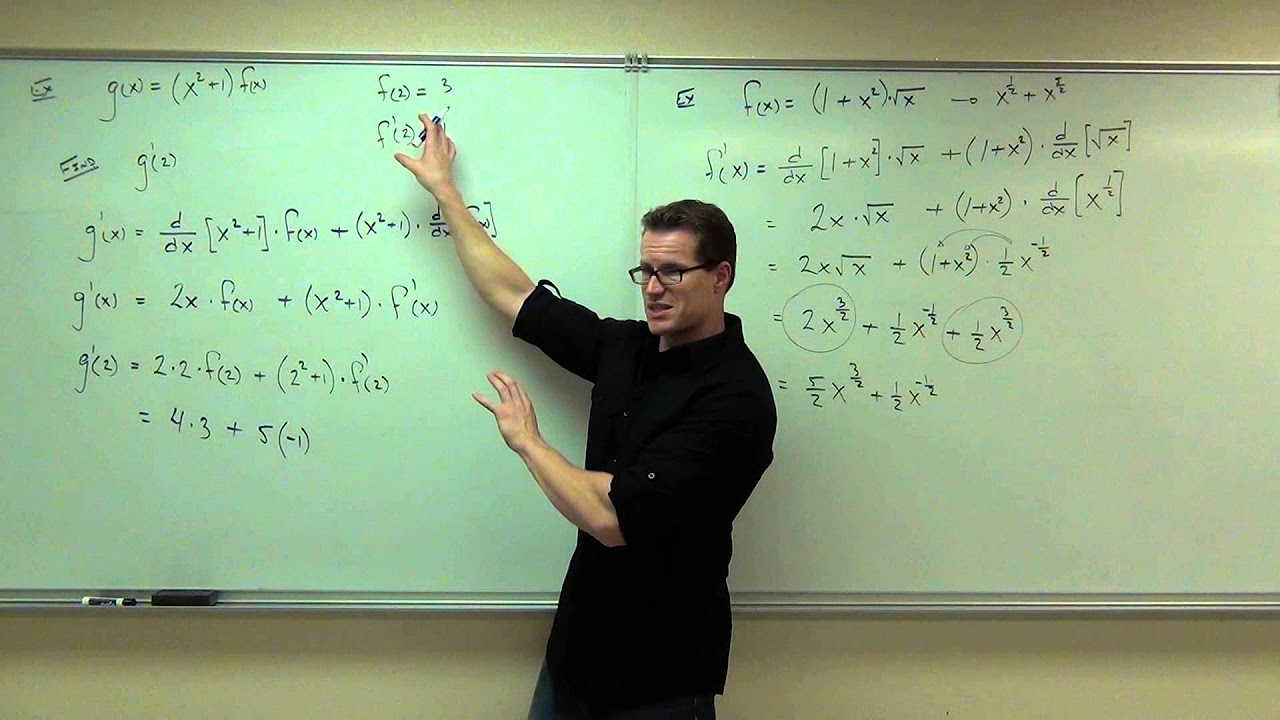
Calculus 1 Lecture 2.3: The Product and Quotient Rules for Derivatives of Functions

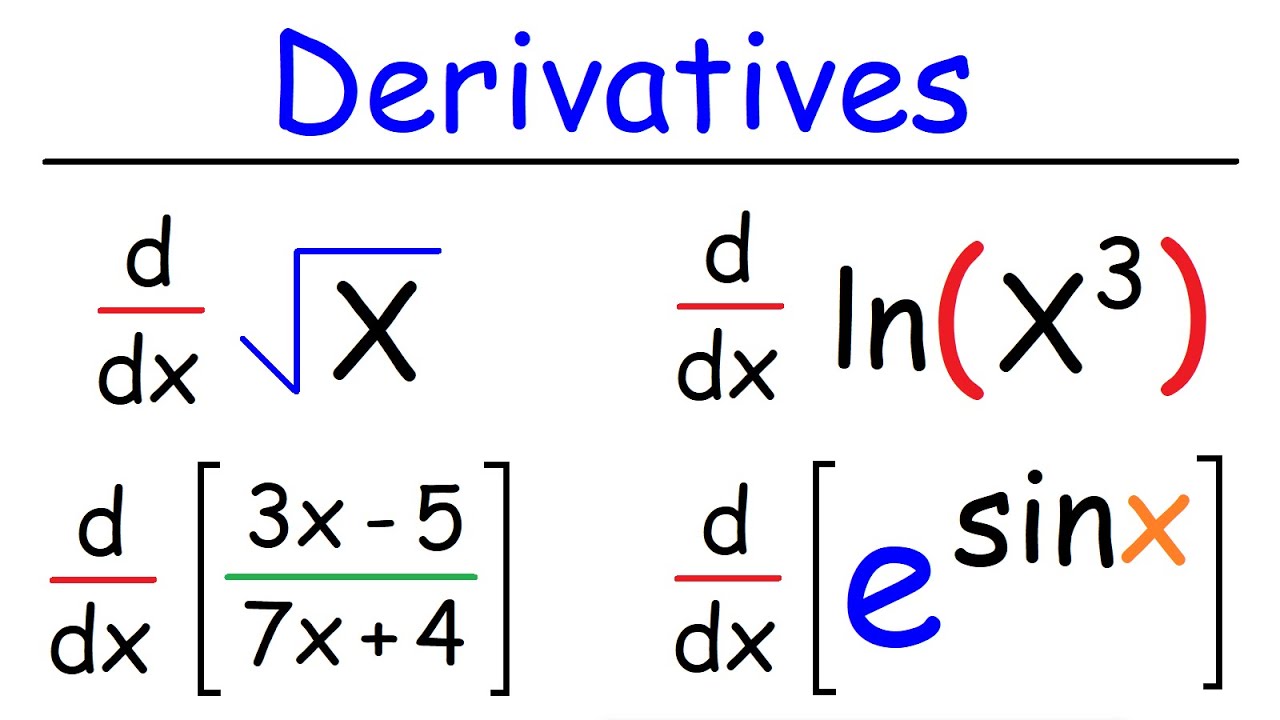
Derivatives for Beginners - Basic Introduction

How to take Derivatives in Calculus - Differentiation Formulas - [1-3]

Business Calculus - Math 1329 - Section 2.3 - Product and Quotient Rules; Higher-order Derivatives

AP Calculus AB and BC Unit 3 Review [Differentiation: Composite, Implicit, and Inverse Functions]

Finding 2nd Derivatives

Related Tags

Math Tutorial Derivatives Differentiation Class 12 Educational Video Mathematics Concept Explanation Step-by-Step Guide Exam Preparation Student Learning