8.01x - Lect 2 - 1D Kinematics - Speed, Velocity, Acceleration

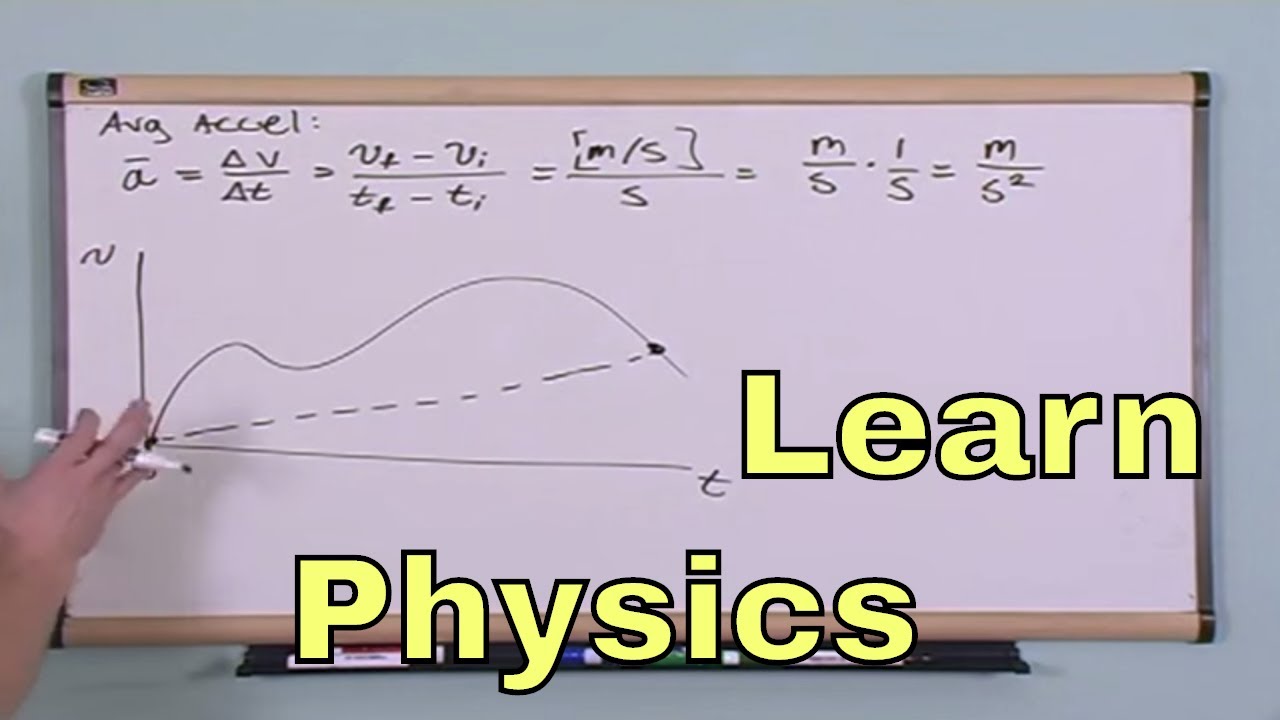
This paragraph introduces the concepts of velocities and accelerations in the context of one-dimensional motion. It begins with a simple example of an object moving along a straight line and defines the average velocity as the change in position divided by the change in time. The distinction between average velocity and instantaneous velocity is highlighted, with the latter being defined at a specific time. The concept of average speed is also introduced, which is the total distance traveled divided by the time taken, and is noted to be different from average velocity as it does not account for direction. The importance of sign conventions in physics is emphasized, and the impact of choosing different reference points for position and direction is discussed.

This section delves deeper into the concepts of average velocity and speed, emphasizing their differences and how they are calculated. It clarifies that while average velocity can be zero if an object returns to its starting point, average speed is not zero as it accounts for the total distance traveled. The paragraph also explains the relationship between instantaneous velocity and the first derivative of the position-time graph, and how to determine when the velocity is zero by looking for the derivative to be zero. The discussion includes the impact of the angle (alpha) on the sign of average velocity and the significance of sign conventions in physics calculations.

This paragraph discusses the practical aspects of measuring average speed and velocity, using the example of a bullet passing through two wires. It explains the importance of accounting for uncertainties in both distance and timing measurements. The text also explores the concept of instantaneous velocity and how it can be understood as the limiting case as time intervals approach zero. The significance of the first derivative of the position-time graph in determining instantaneous velocity is highlighted, and the equation v = dx/dt is introduced as a key formula to remember.

This section introduces the concept of average acceleration, which is defined as the change in velocity over time. It explains how to calculate average acceleration and how it can be positive, negative, or zero depending on the change in velocity. The text also discusses the relationship between average acceleration and the direction of increasing x, and how reversing this direction can change the signs of both velocity and average acceleration. Practical examples involving a tennis ball and objects like a tomato or an egg are used to illustrate the concepts, emphasizing that the magnitude of acceleration, regardless of its sign, can cause objects to break upon impact.

This paragraph focuses on the concept of instantaneous acceleration, which is the acceleration at any given moment in time. It is described as the first derivative of the velocity-time graph and the second derivative of the position-time graph. The text explains how to determine where acceleration is zero, positive, or negative by analyzing the graph and understanding how the angle (alpha) changes. A straightforward example is provided, where the position of an object is given as a function of time, and the velocity and acceleration are derived from it. The example is used to illustrate how to find the times when the object's position, velocity, and acceleration are zero and how to plot the object's trajectory as a parabola.

This section discusses the concept of gravitational acceleration, which is constant and independent of various factors such as the mass, speed, chemical composition, size, and shape of the object, assuming no air drag and vacuum conditions. The general equations for one-dimensional motion under constant acceleration, such as gravity, are presented, and the terms C1, C2, and C3 are explained in relation to initial position, initial velocity, and half of the acceleration, respectively. The gravitational acceleration in Boston is given as 9.80 meters per second squared, and the text prompts the reader to calculate 'g' using two different experiments and to consider the uncertainties in these measurements.

This paragraph describes a demonstration involving the observation of falling objects to test alertness and understanding of the concepts of velocity and acceleration. The demonstration involves dropping an apple and using a strobe light to illuminate the apple at regular intervals, allowing the observer to see the apple's position at different moments during its fall. The observers are asked to estimate where the apple was during each flash and to count the number of flashes seen during a higher frequency strobe. The results of the demonstration are used to illustrate the increasing velocity of the falling object and to test the observers' ability to accurately perceive and count the number of flashes in a short period.

In this final paragraph, the speaker concludes the discussion by humorously advising those who only saw a certain number of flashes during the demonstration to rest over the weekend. The speaker also expresses the need for rest, indicating the end of the session and a light-hearted approach to the challenging material covered.