What does r squared tell us? What does it all mean
TLDRThe video script discusses the concept of R-squared in the context of predicting pizza prices based on the number of toppings. It clarifies that R-squared represents the proportion of variability in the dependent variable (price) that can be explained by the independent variable (number of toppings). The example of two pizzerias, Geno's and Bob's, illustrates how R-squared can be 100% for Geno's, where price variability is solely due to toppings, but only 72% for Bob's, where other factors also affect pricing. The script emphasizes that R-squared does not indicate the model's perfect prediction rate but rather the explanatory power of the model on the variability of the outcome.
Takeaways
- 📈 R-squared (R²) represents the proportion of the variance for a dependent variable that's explained by an independent variable(s) in a regression model.
- 🍕 The example of two pizzerias, Geno's and Bob's, illustrates how R-squared can be used to understand the relationship between the number of toppings and pizza price.
- 🔢 R-squared is the square of the correlation coefficient (R), and it's a statistical measure that helps to assess the goodness of fit of a model.
- 💰 At Geno's, the R-squared value was 100%, indicating that the number of toppings perfectly explains the variability in pizza prices.
- 📊 In contrast, at Bob's, the R-squared value was 72%, showing that while the model explains a significant portion of the price variability, not all of it is accounted for.
- 😕 R-squared is often misinterpreted; it does not indicate the percentage of times a model will predict perfectly, nor does it imply that the model goes through all the data points.
- 🎯 R-squared is a measure of how well the observed outcomes are replicated by the model, without it being a perfect replication.
- 🔄 The residuals are the unexplained portion of the model, representing the differences that the model doesn't account for.
- 🛠️ R-squared should be interpreted as the percentage of variability in the dependent variable (Y) that's explained by the independent variable(s) (X).
- 📈 A higher R-squared value indicates a better fit of the model, but it's important to remember that it's not the sole indicator of a model's usefulness or accuracy.
- 🤔 It's crucial to understand the context and limitations of R-squared when evaluating regression models and drawing conclusions from the data.
Q & A
What is R-squared in the context of the script?
-R-squared, or the square of the correlation coefficient R, is a statistical measure that represents the proportion of the variance for a dependent variable that's explained by an independent variable in a regression model.
How was R-squared calculated in the example of the two pizzerias?
-In the example, R-squared was calculated by fitting a line to a scatterplot of data collected from the pizzerias. The equation derived from the data was used to explain the variability in pizza prices based on the number of toppings.
What are the limitations of interpreting R-squared as a percentage of perfect prediction?
-R-squared does not indicate the percentage of times the model will predict perfectly. It is a measure of how well the independent variable(s) explain the variability in the dependent variable, not the accuracy of each individual prediction.
How did the R-squared values differ between Geno's and Bob's pizzerias?
-At Geno's, the R-squared value was 100%, indicating that the variability in pizza prices could be fully explained by the number of toppings. At Bob's, the R-squared value was 72%, meaning that only 72% of the price variability could be explained by the number of toppings, with other factors also influencing the price.
What does the variability in the script context refer to?
-Variability refers to the differences or fluctuations in a particular variable, in this case, the price of pizzas and the number of toppings. It represents the degree to which outcomes can change or differ from the average or expected value.
What are residuals in the context of the script?
-Residuals are the unexplained portion of the variability in the dependent variable that remains after the regression model has accounted for the relationship between the dependent and independent variables. They represent the differences between the actual data points and the predicted values from the model.
How can R-squared be used to improve a business model like a pizzeria?
-R-squared can help a business understand how much of their product pricing variability is explained by certain factors, like the number of toppings. This insight can be used to refine pricing strategies, manage costs, and make more informed business decisions.
Why is it important to not solely rely on R-squared when evaluating a model?
-R-squared only provides a portion of the information needed to evaluate a model. It does not account for the complexity of the model, potential overfitting, or the presence of other influential factors. A comprehensive evaluation should include other statistical metrics and qualitative considerations as well.
What does the initial fixed price of a pizza (e.g., $10 for cheese) represent in the context of the model?
-The initial fixed price represents a part of the overall pizza price that is not explained by the number of toppings. It is an inherent cost or baseline price that is constant regardless of the variability in toppings.
How can understanding the R-squared value help in making pricing decisions?
-Understanding the R-squared value can help in making pricing decisions by revealing how much of the price variability is linked to specific factors, such as the number of toppings. This can guide decisions on how to structure pricing tiers, set base prices, and determine additional charges for extras.
What is the key takeaway from the script about R-squared interpretation?
-The key takeaway is that R-squared should be interpreted as the percentage of variability in the dependent variable (Y) that is explained by the model, not as the percentage of perfect predictions or the percentage of the entire dependent variable that the model explains.
Outlines
📊 Introduction to R-squared and its Misinterpretations
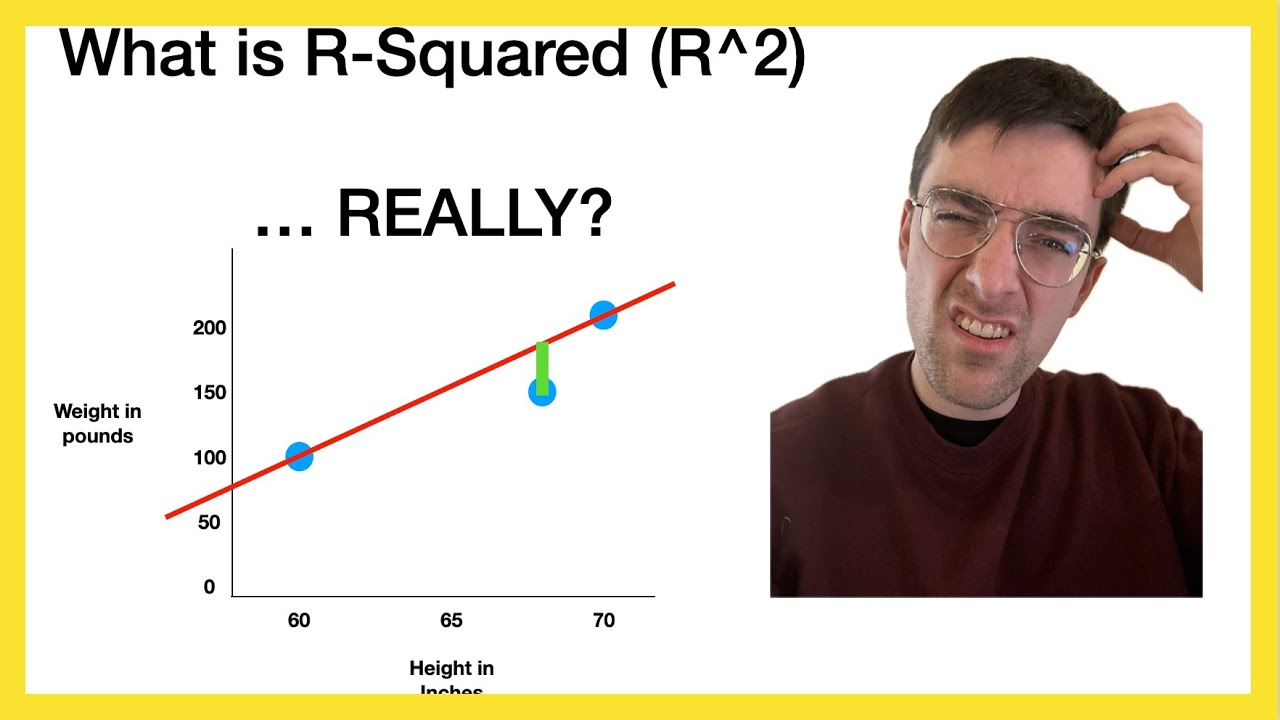
This paragraph introduces the concept of R-squared, which is the square of the correlation coefficient R, used to measure the predictive power of a model. It clarifies common misconceptions about R-squared, emphasizing that it doesn't indicate the percentage of times a model will make perfect predictions. Instead, it illustrates the proportion of variance for the dependent variable (price of pizza in this case) that can be explained by the independent variable (number of toppings). The narrative uses a relatable example of two pizzerias with different pricing models for toppings, highlighting how R-squared values can vary even when the underlying relationships are similar.
🍕 Variability Explained through R-squared in Pizza Toppings
The paragraph delves deeper into the meaning of R-squared by focusing on the concept of variability. It explains that R-squared represents the percentage of variability in the dependent variable (pizza price) that can be explained by the variability in the independent variable (number of toppings). The example of Geno's pizzeria is used to illustrate that 100% of the price variability can be explained by the number of toppings, whereas at Bob's, only 72% of the price variability is explained by the number of toppings. This distinction is crucial in understanding that R-squared does not account for all price differences but rather the proportion of variability that the model can explain. Residuals, or the unexplained portion, are also introduced as a part of the price variability that the model does not account for.
📝 Final Thoughts on Interpreting R-squared
In this paragraph, the speaker aims to clarify the correct interpretation of R-squared values. It emphasizes that R-squared represents the percentage of variability in the dependent variable (Y) that is explained by the model, not the percentage of the entire price or the percentage of perfect predictions. The speaker uses a hypothetical multiple-choice question to highlight the common misunderstanding and corrects it. The summary underscores that R-squared is about the variability in Y explained by the model, not the entire Y or the frequency of perfect predictions. The paragraph concludes with a reiteration of the importance of understanding R-squared in the context of model interpretation and its limitations.
Mindmap
Keywords
💡R-squared
💡Correlation Coefficient (R)
💡Predicting Power
💡Variability
💡Residuals
💡Pizza Toppings
💡Price
💡Regression Model
💡Data Fit
💡Trend
💡Scatterplot
Highlights
R-squared is the square of the correlation coefficient R, which is used to evaluate the predictive power of a model. (Start time: 0s)
The R-squared value indicates the proportion of the variance for the dependent variable that's explained by the independent variables in the model. (Start time: 30s)
R-squared does not represent the percentage of times the model will predict perfectly, nor does it indicate the percentage of points that the model goes through. (Start time: 60s)
The example of two pizzerias, Geno's and Bob's, is used to illustrate the concept of R-squared and its interpretation in the context of price prediction based on the number of toppings. (Start time: 90s)
Geno's pizzeria has an R-squared value of 100%, meaning that 100% of the differences in pizza prices can be explained by the differences in the number of toppings. (Start time: 120s)
Bob's pizzeria has an R-squared value of 72%, indicating that 72% of the price differences can be explained by the variability in the number of toppings, while the remaining 28% is unexplained by the model. (Start time: 210s)
The R-squared value is a measure of how well the observed outcomes are replicated by the model, based on the variability present in the data. (Start time: 240s)
Residuals are the unexplained part of the model, representing the differences that the model does not account for. (Start time: 270s)
An R-squared value of 100% means that the model explains all the variability in the dependent variable, which is rare and indicates a perfect fit. (Start time: 300s)
A lower R-squared value, such as 72%, suggests that while the model explains a significant portion of the variability, there are other factors influencing the outcome that are not captured by the model. (Start time: 330s)
The initial fixed cost, like the base price of a pizza, is not explained by the number of toppings and is not considered in the R-squared calculation. (Start time: 360s)
R-squared should be interpreted as the percentage of variability in the dependent variable that is explained by the model, not as the percentage of the entire dependent variable. (Start time: 390s)
In the context of the pizzeria example, R-squared can help understand the impact of topping prices on pizza costs and identify areas where the model may need improvement. (Start time: 420s)
A high R-squared value does not guarantee perfect predictions, as models are unlikely to be perfect due to various external factors that may influence the outcome. (Start time: 450s)
R-squared is a valuable tool for model evaluation, but it should be used in conjunction with other statistical measures to fully understand the model's performance. (Start time: 480s)
The concept of R-squared is crucial in regression analysis as it provides a clear picture of how well the independent variables are related to the dependent variable. (Start time: 510s)
Understanding R-squared and its limitations is essential for accurate model interpretation and for making informed decisions based on the model's predictions. (Start time: 540s)
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: