R-squared, Clearly Explained!!!

StatQuest with Josh Starmer
18 Nov 202211:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video script from Stat Quest introduces R-squared, a metric of correlation that is easily computed and interpreted. It explains how R-squared, the square of the correlation coefficient R, quantifies the proportion of variance for one variable that's predictable from the other. The script uses examples with mouse weight and size, and mouse weight and time spent sniffing a rock, to illustrate how R-squared can range from 0 to 1, indicating the percentage of total variation explained by the relationship. It highlights the ease of interpretation and the significance of R-squared in understanding the strength of a correlation compared to the raw R value.

Takeaways
  • 📊 R-squared (R²) is a metric of correlation that is easy to compute and interpret.
  • 🔄 R-squared is similar to the correlation coefficient (R), but offers easier interpretation.
  • 📈 An R-squared value of 1 indicates that the model explains all the variation in the data, while 0 means it explains none.
  • 🔢 R-squared is calculated by dividing the sum of squared differences between actual data points and their mean by the sum of squared differences between actual data points and the fitted line.
  • 🐭 The example of mouse weight and size demonstrates how R-squared can quantify the goodness of fit of a model.
  • 📉 When comparing unrelated variables (e.g., mouse weight and time spent sniffing a rock), R-squared can show how little the relationship explains the data variation.
  • 🅿️ A high R-squared value (e.g., 0.9) means 90% of the data variation is explained by the relationship between variables.
  • 🅰️ A low R-squared value (e.g., 0.01) indicates that only 1% of the variation is explained, and other factors likely account for most of the data's variability.
  • 🔢 The relationship between R and R-squared is that R-squared is the square of the R value (e.g., R=0.9 leads to R²=0.81).
  • ⏩ Converting R to R-squared in your head can provide a clearer understanding of how much variation is explained by the relationship.
  • 🚫 R-squared does not indicate the direction of the correlation, as squared values are always positive.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is r-squared (R²), a metric of correlation that is easy to compute and interpret in statistics.

  • How is r-squared related to the standard metric of correlation, R?

    -R-squared is related to R as it is the square of the correlation coefficient (R). It provides a percentage that represents the proportion of the variance for the dependent variable that's explained by the independent variables in a regression model.

  • Why might R-squared be preferred over R in interpreting a correlation?

    -R-squared is often preferred because it provides an easier interpretation as it represents the proportion of variance explained by the model, and its value ranges from 0 to 1, making it intuitive to understand the strength of the correlation.

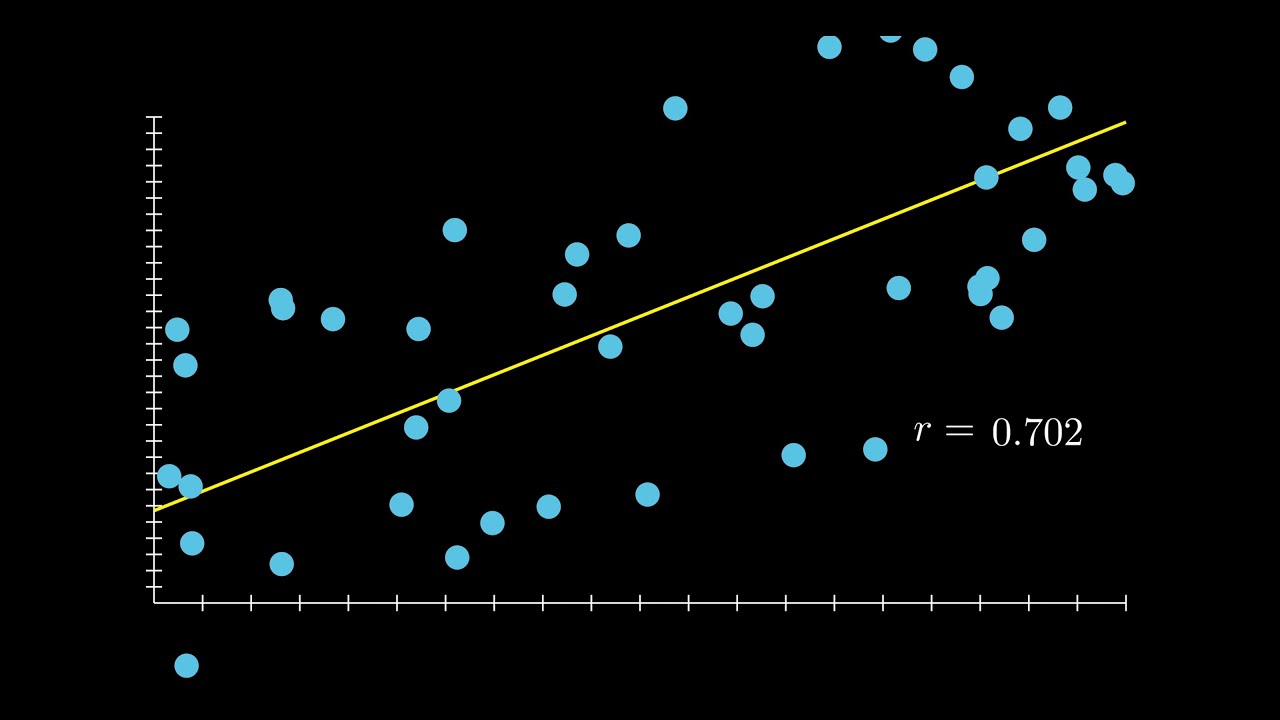
  • What does an R-squared value of 0.7 signify?

    -An R-squared value of 0.7 means that 70% of the variance in the dependent variable can be explained by the relationship with the independent variable(s) in the regression model.

  • How is the variation around the mean calculated in the video example?

    -The variation around the mean is calculated by summing the squared differences between each data point's weight and the mean weight of all data points.

  • What is the formula for calculating R-squared?

    -The formula for calculating R-squared is (1 - (Sum of squared differences around the regression line / Sum of squared differences around the mean)). It essentially measures how much better the regression line fits the data compared to simply using the mean.

  • What does a low R-squared value, like 0.06, indicate?

    -An R-squared value of 0.06 indicates that only 6% of the variance in the dependent variable can be explained by the relationship with the independent variable(s), suggesting a weak explanatory power of the model.

  • How can you interpret a statistically significant R-squared value of 0.9?

    -A statistically significant R-squared value of 0.9 indicates that 90% of the variation in the data can be explained by the relationship between the variables, which is a strong correlation.

  • What does the direction of correlation mean in the context of R-squared?

    -R-squared does not indicate the direction of the correlation because it is a squared value and cannot be negative. However, the direction (positive or negative) can be inferred from the context or by looking at the original R value before squaring.

  • How can you relate R-squared back to R?

    -To relate R-squared back to R, you square the R value. For example, if R is 0.9, then R-squared is 0.9 * 0.9 = 0.81, which means 81% of the variation is explained by the relationship.

  • What is the significance of R-squared in statistical analysis?

    -The significance of R-squared in statistical analysis is that it provides a clear and quantifiable measure of how much of the variance in one variable can be explained by the variance in another variable(s), which helps in understanding the strength and effectiveness of the relationship in a model.

Outlines
00:00
📊 Introduction to R-Squared

This paragraph introduces the concept of R-squared as a metric of correlation, emphasizing its ease of computation and intuitive interpretation. It contrasts R-squared with the standard correlation coefficient (R), highlighting the benefits of R-squared in terms of its interpretability and calculation. The paragraph sets the stage for a deeper exploration of R-squared by discussing its significance in understanding the relationship between two quantitative variables, such as weight and size, and how it can be used to predict outcomes based on known variables.

05:02
🧮 Calculation and Interpretation of R-Squared

This section delves into the process of calculating R-squared and interpreting its value. It begins by explaining the concept of variation around the mean and how it is calculated. The paragraph then illustrates the calculation of variation around a fitted line (the 'Blue Line' in the example) and how this relates to R-squared. The explanation includes a step-by-step example where mouse weight is plotted against mouse size, and the variation around the mean and the Blue Line is calculated. The resulting R-squared value is then used to determine the percentage of variation explained by the relationship between the two variables.

10:03
🔢 Understanding the Practical Implications of R-Squared

The final paragraph discusses the practical implications of R-squared values in statistical analysis. It explains how R-squared can be used to gauge the strength of the relationship between two variables and the proportion of variation explained by this relationship. The paragraph contrasts examples with high and low R-squared values to demonstrate their significance. It also touches on the limitations of R-squared, such as its inability to indicate the direction of correlation. The section concludes by reinforcing the importance of R-squared in statistical analysis and encourages viewers to apply this knowledge in their understanding of future statistical concepts.

Mindmap
Keywords
💡R-squared
R-squared, or coefficient of determination, is a statistical measure that represents the proportion of the variance for a dependent variable that's explained by an independent variable or variables in a regression model. It is a number between 0 and 1, where a higher value indicates a better fit of the model. In the video, r-squared is used to quantify how well the size of a mouse predicts its weight, with an r-squared value of 0.81 indicating that 81% of the variation in weight can be explained by size.
💡Correlation
Correlation refers to a statistical relationship between two variables that describes how they change in relation to each other. A high positive correlation (close to 1) indicates that as one variable increases, the other also increases, while a high negative correlation (close to -1) indicates that as one variable increases, the other decreases. In the context of the video, correlation is discussed in relation to r-squared, emphasizing that while correlation values near 1 or -1 indicate a strong relationship, r-squared provides a clearer interpretation of the strength of that relationship.
💡Regression Line
A regression line, also known as the line of best fit, is a straight line that best represents the data on a scatter plot. It is calculated using a regression analysis, which aims to find the line where the sum of the squares of the vertical distances (residuals) from the data points to the line is minimized. In the video, the regression line is used to predict mouse weight based on size, illustrating that fitting a line to the data can significantly improve predictions over simply using the mean.
💡Variation
Variation refers to the differences in data from the mean or expected value. In a dataset, variation can be observed as the spread or dispersion of data points around the mean. The video discusses calculating variation around the mean and around a regression line, emphasizing that the goal is to reduce this variation by finding patterns or relationships that can explain the data points.
💡Mean
The mean, or average, is a central tendency measure that is calculated by adding up all the values in a dataset and dividing by the number of values. It represents the typical or central value in a set of data. In the video, the mean weight of mice is calculated and used as a baseline to compare against the variation around the regression line, highlighting that the mean is a simple predictor but may not capture the relationship between variables as effectively as a regression line.
💡Sum of Squared Differences
The sum of squared differences is a calculation used in statistical analysis to measure the total amount of variation or dispersion of a set of values. It involves taking the difference between each value and the mean, squaring the result, and then summing these squared differences. This concept is crucial in the video when explaining how to calculate the variation around the mean and the regression line, as it forms the basis for calculating r-squared.
💡Statistical Significance
Statistical significance is a measure that determines whether an observed result could have occurred by chance. It is typically assessed using a p-value or confidence intervals. In the context of the video, statistical significance is mentioned in relation to r-squared values, emphasizing that a high r-squared value indicates that the observed relationship between variables is unlikely to be due to random chance and thus is a meaningful finding.
💡Data Points
Data points are individual values or observations represented in a dataset, often depicted as dots on a graph or chart. Each data point corresponds to the specific values of the variables being measured. In the video, data points are used to illustrate the variation around the mean and the regression line, showing how the position and distribution of these points can be analyzed to understand the relationship between variables.
💡Predict
To predict, in a statistical context, means to use a model or relationship to estimate a value for a dependent variable based on known values of one or more independent variables. The video demonstrates this by using the size of a mouse to predict its weight through a regression line, highlighting the utility of statistical models in making predictions about data.
💡Positive Correlation
A positive correlation is a relationship between two variables where they tend to increase or decrease together. In other words, as one variable goes up, the other also goes up, and vice versa. The video mentions positive correlation in the context of the relationship between mouse size and weight, where a larger size is associated with a heavier weight.
💡Negative Correlation
A negative correlation is a relationship between two variables where one variable increases as the other decreases. This type of correlation indicates an inverse relationship. Although not explicitly mentioned in the video, the concept is relevant when discussing the direction of the relationship between variables, as r-squared values cannot indicate whether the correlation is positive or negative, only the strength and proportion of the explained variation.
Highlights

R-squared (r^2) is a metric of correlation that is easy to compute and intuitive to interpret.

R-squared is similar to the standard metric of correlation, R, but offers easier interpretation.

An R-squared value of 0.7 indicates 1.4 times better correlation than R-squared at 0.5.

R-squared is calculated by comparing the variation around the mean to the variation around a fitted line.

The equation for R-squared is derived by dividing the difference in variation between the mean and the fitted line by the variation around the mean.

R-squared ranges from 0 to 1 and represents the percentage of variation explained by the relationship between two variables.

An R-squared value of 0.81 or 81% indicates that 81% of the total variation is explained by the size-weight relationship.

Comparing two uncorrelated variables, R-squared can show the percentage of variation explained by each relationship.

An R-squared of 0.06 or 6% indicates that only 6% of the total variation is explained by the sniff-weight relationship.

A statistically significant R-squared of 0.9 means that 90% of the variation in the data is explained by the relationship between the two variables.

A statistically significant R-squared of 0.01 means that only 1% of the variation in the data is explained by the relationship, with 99% unaccounted for.

R-squared is the square of R, making it easier to understand the proportion of variation explained by squaring the correlation coefficient.

R-squared does not indicate the direction of the correlation, as squared numbers are never negative.

R-squared is preferred over plain R because it provides a clearer understanding of the proportion of variation explained in the data.

The video provides a step-by-step example of calculating R-squared and interpreting its results.

Understanding R-squared allows for better evaluation of the significance and strength of relationships between variables.

Transcripts

Browse More Related Video

R-squared, Clearly Explained!!!

Correlation and Coefficient of Determination in 3 Minutes

R Squared or Coefficient of Determination | Statistics Tutorial | MarinStatsLectures

What is R-Squared (R^2) ... REALLY?

Linear Regression in R, Step-by-Step

Math 119 Chapter 10 Part 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Data AnalysisR-squared InterpretationCorrelation MetricsStatistical ConceptsPredictive ModelingGenetics ResearchEducational ContentData VisualizationQuantitative AnalysisStatistical Significance