Example: Correlation coefficient intuition | Mathematics I | High School Math | Khan Academy
TLDRThe video script discusses the concept of correlation coefficients, emphasizing on their role in measuring the relationship between two variables through a linear model. It explains the meaning of positive and negative correlations using hypothetical data points and scatterplots. The script also illustrates how to visually assess the correlation by matching scatterplots to given correlation coefficients, highlighting the imperfections of fitting a linear model to real-world data. The key takeaway is understanding the intuition behind correlation coefficients without delving into the calculation process.
Takeaways
- 📊 Correlation coefficients measure how well a linear model can describe the relationship between two variables.
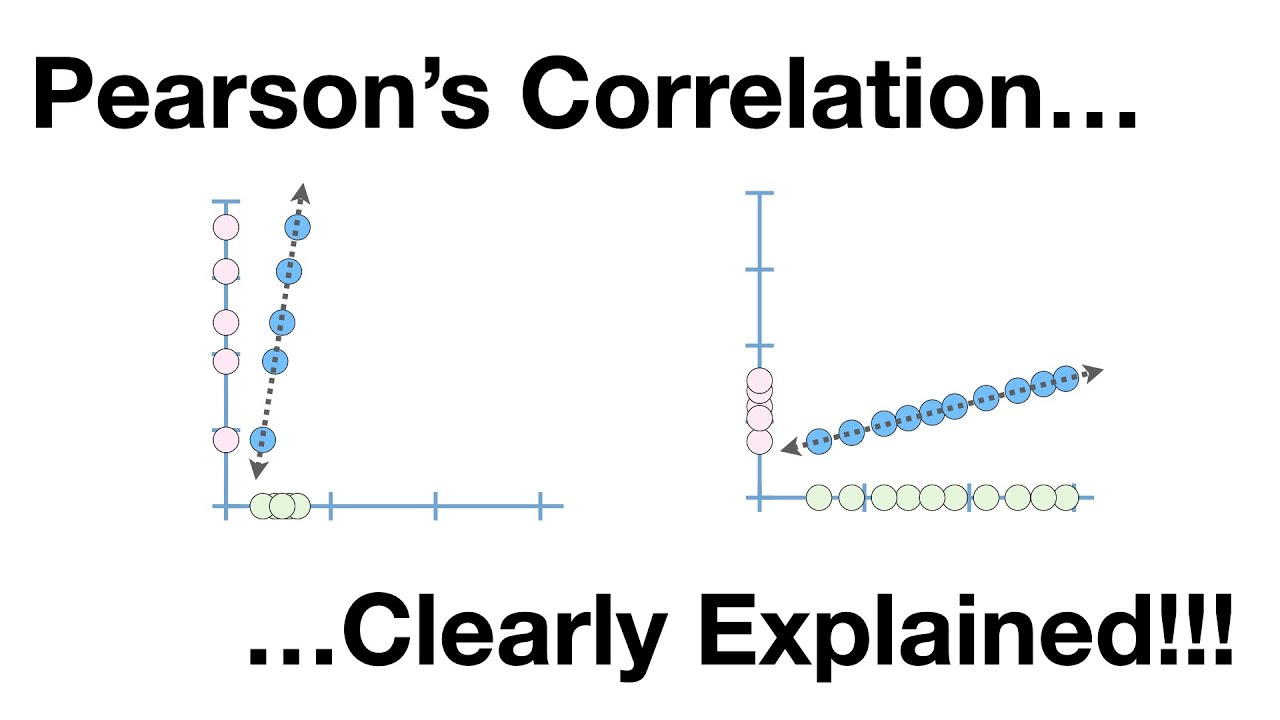
- 🔍 An r value of 1 indicates a perfect positive correlation, where both variables increase or decrease together.
- 🔽 A negative r value of -1 represents a perfect negative correlation, where one variable increases as the other decreases.
- 🔄 For an r value of 0, there is no linear correlation between the variables; a linear model does not fit the data well.
- 👀 The exercise involves matching correlation coefficients to scatterplots based on visual intuition rather than calculation.
- 🎯 When x is low and y is high, or x is high and y is low, the correlation is likely negative.
- 📈 A positive correlation is suggested when both variables show a pattern of increase or decrease together.
- 🤔 Scatterplots can be imperfect, and fitting a linear model to them may not always result in a perfect match.
- 🔢 The process of matching correlation coefficients to scatterplots involves eyeballing the data and assessing the strength of the linear relationship.
- 🏋️♂️ The strength of the correlation (r value) depends on how closely the data points align with a potential linear trend.
Q & A
What is the main purpose of the exercise described in the transcript?
-The main purpose of the exercise is to develop an intuition for the correlation coefficient by matching given correlation coefficients to various scatterplots, without focusing on the exact calculation method.
What does a correlation coefficient attempt to measure?
-A correlation coefficient attempts to measure how well a linear model can describe the relationship between two variables.
What would a scatterplot with an r of 1 look like?
-A scatterplot with an r of 1 would show a perfect positive correlation, where as one variable increases, the other also increases, and they fit well on a straight line.
How does a scatterplot with an r of -1 differ from one with an r of 1?
-A scatterplot with an r of -1 would show a perfect negative correlation, where as one variable increases, the other decreases, and they also fit well on a straight line but in opposite directions.
What kind of scatterplot would have an r of 0?
-A scatterplot with an r of 0 would show no linear correlation, where the data points are scattered randomly and do not fit a linear model well.
How does the speaker decide which correlation coefficient to match with a given scatterplot?
-The speaker decides by eyeballing the scatterplot and assessing the general trend and strength of the relationship, then chooses the correlation coefficient that best fits the observed pattern.
What is the speaker's approach to fitting a linear model to an imperfect dataset?
-The speaker uses their intuition to assess the general trend in the data points and tries to visualize a line that would minimize the distances from the points to the line, understanding that few real-world datasets will perfectly sit on a line.
Why does the speaker feel that r equals negative 0.72 is a good match for scatterplot A?
-The speaker feels that r equals negative 0.72 is a good match for scatterplot A because there is a clear negative correlation, with a strong pattern of large y values corresponding to small x values and vice versa.
How does the speaker determine that scatterplot B has a better fit with a higher positive correlation coefficient than scatterplot D?
-The speaker determines that scatterplot B has a better fit because a linear model works better for it, with fewer data points far away from the line compared to scatterplot D, which has more points off the line despite showing a positive correlation.
What is the rationale behind choosing r equals 0.65 for scatterplot D?
-The rationale for choosing r equals 0.65 for scatterplot D is that, although there is a positive correlation, there are several data points that are far away from the model, indicating that the linear model does not fit the data as well as it does for scatterplot B.
How does the speaker's approach to this exercise help in understanding the concept of correlation coefficients?
-The speaker's approach helps in understanding the concept of correlation coefficients by visually assessing the relationship between variables in different scatterplots and matching them with appropriate coefficients, thus providing a practical and intuitive grasp of the concept.
Outlines
📊 Correlation Coefficient Intuition and Linear Model Analysis
This paragraph delves into the concept of correlation coefficients and their role in measuring the relationship between two variables. It explains that the main idea is to assess how effectively a linear model can describe this relationship. The speaker uses the example of direct proportionality where an increase in one variable corresponds to an increase in the other, illustrating a positive correlation with an r value of 1. Conversely, a negative correlation is described where an increase in one variable leads to a decrease in the other, with an r value of -1. The paragraph also touches on the scenario where there is no clear linear relationship, represented by an r value of 0. The speaker then proceeds to visually match different scatterplots with their corresponding correlation coefficients based on the strength and direction of the relationships observed in the data points, emphasizing the use of intuition over exact calculation at this stage.
📈 Evaluating Scatterplots and Fitting Linear Models
In this paragraph, the speaker continues the discussion on scatterplots and the fitting of linear models to data. The focus is on evaluating the strength and direction of the relationships between variables in different scatterplots. The speaker assesses the positive correlation in scatterplot B, noting that it fits well with a linear model, whereas scatterplot D, despite showing a positive correlation, has more data points远离 the line, indicating a weaker fit. The speaker also revisits scatterplot A, considering its negative correlation and choosing the most appropriate correlation coefficient based on the observed data trend. The paragraph emphasizes the imperfect nature of fitting linear models to real-world data and the process of visually estimating the correlation coefficients for different scatterplots.
Mindmap
Keywords
💡Correlation Coefficient
💡Linear Model
💡Scatterplot
💡Positive Correlation
💡Negative Correlation
💡Intuition
💡Data Points
💡Eyeballing
💡Fit
💡Trend
💡Direction
Highlights
The main idea of correlation coefficients is to measure how well a linear model can describe the relationship between two variables.
A perfect positive correlation is represented by an r value of 1, where both variables increase or decrease together.
A perfect negative correlation is represented by an r value of -1, where one variable increases as the other decreases.
An r value of 0 indicates no linear correlation, where the data points do not follow a clear linear pattern.
The exercise involves matching correlation coefficients to scatterplots without calculating them, but by using intuition.
Scatterplot A shows a negative correlation with a strong trend, suggesting an r value close to negative 1.
Scatterplot B exhibits a positive correlation, with a reasonable fit to the data points, suggesting an r value between 0.65 and 0.84.
Scatterplot C appears non-correlated with no clear pattern, suggesting an r value close to 0.
Scatterplot D has a positive correlation, but the linear model does not fit as well as it does for Scatterplot B.
The process of fitting a linear model to data involves minimizing the distances from the points to the line.
In real-world scenarios, data rarely sits perfectly on a line, making the fitting process imperfect.
The exercise aims to develop an intuitive understanding of correlation coefficients before learning the exact calculation methods.
Eyeballing the data and understanding the general trend is a method to approximate correlation coefficients without calculation.
The transcript provides a visual and intuitive explanation of how correlation coefficients relate to scatterplots.
The example of Scatterplot A with a negative correlation demonstrates how to visually identify and match the correlation coefficient.
For Scatterplot B, the positive correlation and the quality of the linear model fit help in choosing the appropriate correlation coefficient.
The transcript illustrates the challenge of fitting a linear model to data with no clear pattern, as seen in Scatterplot C.
Transcripts
Browse More Related Video

Introduction to Correlation & Regression, Part 1

Statistics 101: Understanding Correlation

Correlation Coefficient

Correlation Doesn't Equal Causation: Crash Course Statistics #8
Pearson's Correlation, Clearly Explained!!!
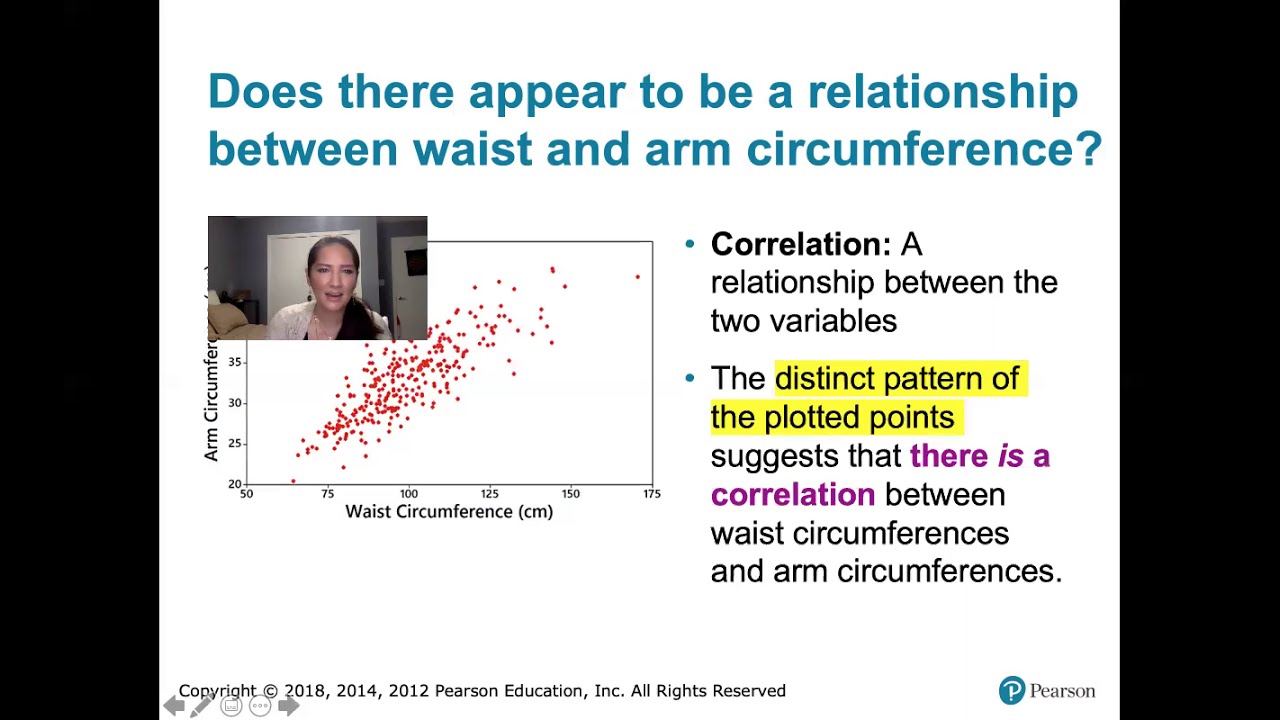
10.1.1 Correlation - Linear, Nonlinear, Positive Linear, and Negative Linear Correlation Defined
5.0 / 5 (0 votes)
Thanks for rating: