Projectile Motion Time of Flight Formula Derivation

Guru Tutor
4 Sept 201904:41
EducationalLearning
32 Likes 10 Comments

TLDRThis video script presents a clear and concise tutorial on deriving the time-of-flight formula for projectile motion in physics. It begins with an introduction to the concept of time-of-flight, which is the duration a projectile takes to return to ground level from where it was launched. The script assumes prior knowledge of six basic projectile motion equations and proceeds to derive the formula using one of these equations. By setting the initial and final vertical positions to zero (ground level) and solving for time, the script arrives at the time-of-flight formula: T = (2 * V0 * sin(theta)) / G, where T is the time of flight, V0 is the initial velocity, theta is the launch angle, and G is the acceleration due to gravity. The explanation is methodical and engaging, making it an excellent resource for those interested in understanding the physics behind projectile motion.

Takeaways
  • 📌 The time-of-flight refers to the duration a projectile takes to reach the ground after being fired from the ground level.
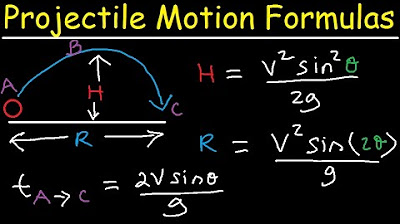
  • 📐 The vertical position formula for projectile motion is used to derive the time-of-flight: Y = V₀T * sin(θ) - 0.5 * G * T².
  • 🔄 The formula is derived assuming no air resistance and that the projectile is fired from and returns to ground level.
  • 🚀 To find the time-of-flight, the initial and final positions are assumed to be at ground level (Y = 0).
  • ⏱ The time-of-flight (capital T) is when the projectile returns to the ground level after being fired.
  • 🔢 The equation to solve for time-of-flight is 0 = V₀T * sin(θ) - 0.5 * G * T², with T = 0 representing the initial position.
  • 🌟 Factoring out T from the equation helps to find the two instances when the projectile is at ground level.
  • 🎯 The time-of-flight is not interested in T = 0 (initial position), but the other value which represents the projectile returning to the ground.
  • 📈 The final derived formula for time-of-flight is T = (2 * V₀ * sin(θ)) / G.
  • 🔄 This formula applies to projectile motion scenarios where the object is launched and returns to the same vertical level (e.g., ground level).
  • 📚 Understanding the time-of-flight formula is crucial for analyzing and predicting the behavior of projectiles in physics.
Q & A

  • What is the definition of time-of-flight in the context of projectile motion?

    -The time-of-flight refers to the duration in seconds it takes for a projectile to reach the ground after being fired from the ground level and returning to the same level.

  • What are the six basic projectile motion equations mentioned in the script?

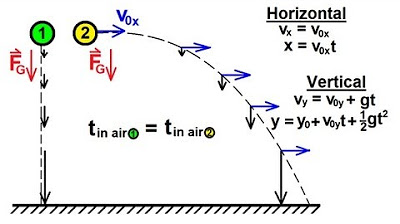
    -The script does not list all six equations explicitly but refers to them as the foundational understanding required to understand the time-of-flight formula derivation. These typically include equations for horizontal range, maximum height, time of flight, and the equations of motion for both horizontal and vertical components.

  • What is the formula used in the script to represent the vertical position of a projectile?

    -The formula used to represent the vertical position of a projectile is given by the equation: y = V₀t * sin(θ) - 0.5 * g * t², where y is the vertical position, V₀ is the initial velocity, θ is the launch angle, t is time, and g is the acceleration due to gravity.

  • What are the assumptions made when deriving the time-of-flight formula?

    -The assumptions made are that the projectile is launched from ground level and returns to the same level, and that the only forces acting on the projectile are gravity and the initial velocity components in the horizontal and vertical directions.

  • How is the time-of-flight formula derived from the vertical position equation?

    -The time-of-flight formula is derived by setting the vertical position y to zero (since the projectile returns to ground level) and solving the resulting quadratic equation for time t. The formula is derived by isolating t and simplifying the equation.

  • What does the time-of-flight formula look like?

    -The time-of-flight formula is given by: T = (2 * V₀ * sin(θ)) / g, where T is the time of flight, V₀ is the initial velocity, θ is the launch angle, and g is the acceleration due to gravity.

  • Why are there two values for time in the context of the time-of-flight?

    -There are two values because the projectile is at ground level twice - once when it is initially launched and once when it returns. The formula calculates the time for the second instance, which is the time of interest.

  • How does the script address the fact that there are two possible times of flight?

    -The script acknowledges that there are two times when the projectile is at ground level but focuses on the second instance, which is the time from launch to when it returns to the ground.

  • What is the significance of the sine function in the time-of-flight formula?

    -The sine function is significant because it relates the launch angle θ to the vertical component of the initial velocity V₀, which directly affects the time it takes for the projectile to return to ground level.

  • How does the acceleration due to gravity (g) affect the time-of-flight?

    -The acceleration due to gravity (g) is a factor in the time-of-flight formula, indicating that the time it takes for a projectile to return to the ground is inversely proportional to the gravitational acceleration. A higher g value would result in a shorter time of flight.

  • What is the role of the initial velocity (V₀) in the time-of-flight formula?

    -The initial velocity (V₀) is a critical factor in determining the time-of-flight. It directly influences the vertical motion of the projectile, and its value affects how high and how far the projectile will travel before returning to the ground.

Outlines
00:00
📚 Deriving the Time-of-Flight Formula for Projectile Motion

This paragraph introduces the topic of deriving the time-of-flight formula for projectile motion in physics. It mentions a prerequisite presentation on six basic projectile motion equations and encourages the viewer to watch it first. The paragraph then explains the concept of time of flight, which is the duration a projectile takes to reach the ground after being fired from it. The explanation involves using one of the six basic projectile motion formulas to determine the vertical position of the projectile as it flies through the air. The goal is to find the time (denoted as capital T) when the projectile returns to ground level, assuming it was fired from there. The paragraph sets up the equation and describes the process of substituting values to solve for the time of flight.

Mindmap
Keywords
💡Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and moves under the influence of gravity and air resistance. In the context of the video, it is the study of how an object moves when thrown near the Earth's surface, taking into account the vertical and horizontal components of its trajectory.
💡Time-of-Flight
Time-of-flight is the total time duration from the moment a projectile is launched until it returns to its original height or reaches the ground. In the video, the time-of-flight is the main focus, as the tutorial aims to explain how to calculate the time it takes for a projectile to land after being thrown.
💡Vertical Position
The vertical position is the height or depth of an object in relation to a reference point, often the ground level. In the video, the vertical position of the projectile is described by a mathematical equation that shows how the object's height changes over time as it moves through the air.
💡Initial Velocity
Initial velocity is the speed at which an object is moving when it is first launched or set into motion. In the context of the video, the initial velocity is a crucial factor in determining the trajectory and time-of-flight of the projectile, as it affects both the distance and time the object will travel.
💡Angle of Projection
The angle of projection is the angle at which a projectile is launched or thrown. It is a key factor in determining the trajectory of the projectile and influences both the range and height the object will achieve. The sine of this angle is used in the time-of-flight formula to calculate the flight duration.
💡Acceleration Due to Gravity
Acceleration due to gravity (G) is the constant rate at which objects near the Earth's surface accelerate downward due to the Earth's gravitational pull. It is a fundamental force in the study of projectile motion, as it dictates the vertical component of the object's velocity and its change in height over time.
💡Formula Derivation
Formula derivation is the process of obtaining a mathematical relationship or equation through logical steps and mathematical manipulations. In the video, the derivation of the time-of-flight formula is the primary educational objective, guiding viewers through the steps required to arrive at the equation from basic principles of physics.
💡Equations of Motion
Equations of motion are mathematical expressions that describe the behavior of an object in motion. They are essential tools in physics for predicting and analyzing the movement of objects under various forces. The video script focuses on one specific equation of motion related to projectile motion.
💡Ground Level
Ground level is the reference point from which the vertical position of an object is measured in projectile motion. It is assumed to be the starting and ending point for the object's flight. In the video, the concept of ground level is used to define the conditions for calculating the time-of-flight, as the object is launched from and returns to this level.
💡Algebraic Manipulation
Algebraic manipulation is the process of rearranging and combining mathematical terms to solve equations. It involves using properties of algebra, such as factoring and canceling, to isolate variables and find solutions. In the video, algebraic manipulation is used to derive the time-of-flight formula from the vertical position equation.
💡Trajectory
Trajectory is the path or course followed by an object in motion. In the context of projectile motion, it refers to the curved path of the projectile through the air, which is determined by the initial conditions and the forces acting on the object, such as gravity.
Highlights

Deriving the time-of-flight formula for projectile motion is the main focus of the tutorial.

The tutorial assumes prior knowledge of six basic projectile motion equations in physics.

The time of flight refers to the duration in seconds it takes for a projectile to reach the ground after being fired.

The tutorial uses one of the six basic projectile motion formulas to derive the time-of-flight formula.

The vertical position of the projectile as it flies through the air is represented by a specific formula.

The time T starts at zero and increases as the projectile follows its path.

The projectile has a position (X, Y) as it travels, with Y representing the vertical position.

The time when the projectile reaches the ground again is denoted as capital T.

At ground level, Y is assumed to be zero, simplifying the equation.

The equation to solve for the time of flight involves substituting Y with zero and expressing it in terms of T.

By factoring out capital T, the equation can be simplified to solve for the time of flight.

The time-of-flight formula is derived by isolating T and simplifying the equation.

The derived formula for time of flight is 2 * Vnaught * sine(theta) / G.

The initial velocity of the projectile is factored into the time-of-flight calculation.

The angle theta at which the projectile is fired is also a crucial component of the formula.

Acceleration due to gravity, represented by G, is a key factor in determining the time of flight.

The tutorial concludes by presenting the final time-of-flight formula in a clear and concise manner.

The practical application of the time-of-flight formula is emphasized for understanding projectile motion.

Transcripts

Browse More Related Video

Projectile Motion Maximum Height Formula Derivation

Introduction to Projectile Motion - Formulas and Equations

Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y

College Physics 1: Lecture 12 - Projectile Motion

Projectile Launched of a Cliff

Consolidation: Projectile Motion Calculations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsTutorialProjectileMotionTimeOfFlightDerivationEducationalContentMathematicalAnalysisKinematicsAccelerationDueToGravityTrigonometryPhysicsEducation