Resistivity - Required Practical - A-level Physics

Science Shorts
31 Dec 201807:55
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script offers a detailed walkthrough of an A-level physics practical investigation to determine the resistivity of a wire by exploring how resistance changes with length or cross-sectional area. The tutorial begins with the theoretical basis for resistivity, explaining equations and terminology, before moving on to the experimental setup involving a circuit with an ammeter, voltmeter, and variable resistor. The presenter emphasizes the importance of keeping the current below 1 amp to prevent the wire from heating, which could affect resistivity readings. Various aspects of the experiment, such as measuring voltage, current, and calculating resistance, are covered alongside considerations for accurate data collection and analysis, including uncertainty calculation and control variables. The video concludes with advice on plotting results and interpreting gradients to find the wire's resistivity, offering a comprehensive guide for students conducting physics experiments.

Takeaways
  • πŸ“š The experiment aims to investigate the relationship between a wire's resistance and its length and cross-sectional area, ultimately determining the wire's resistivity.
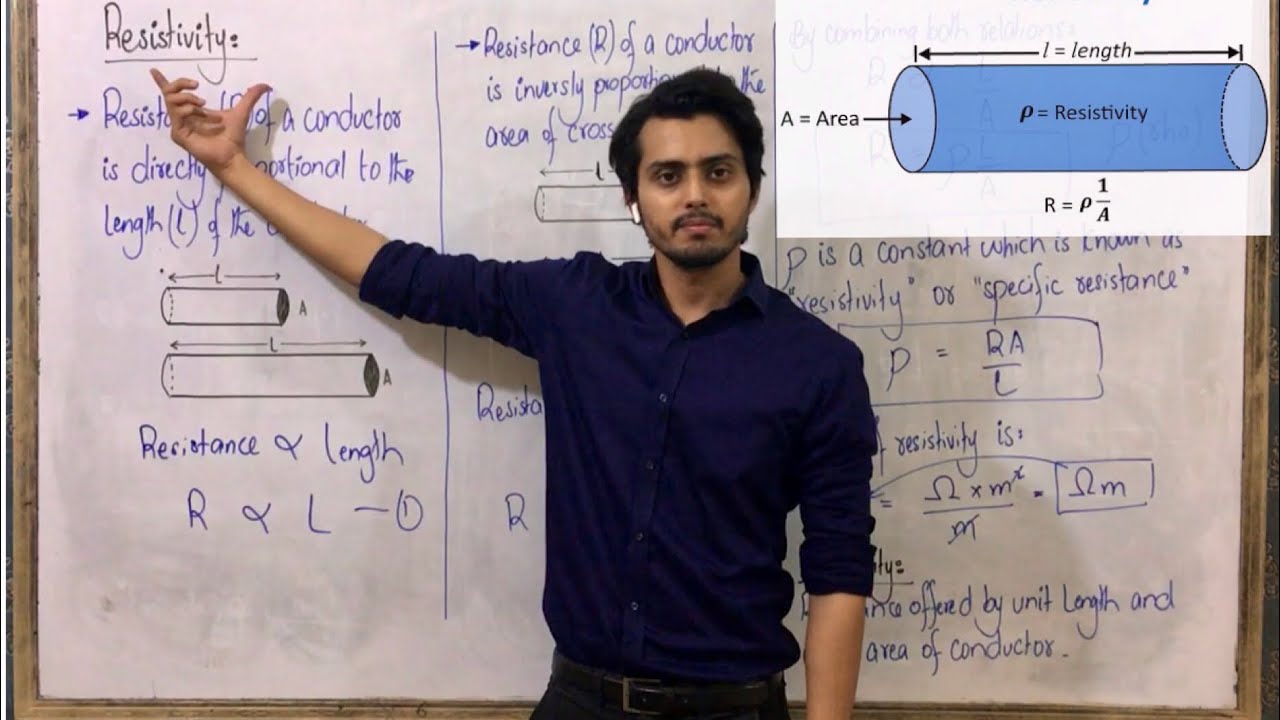
  • πŸ§ͺ The resistivity (Rho) is calculated using the formula Rho = R * A / L, where R is resistance, A is cross-sectional area, and L is length.
  • πŸ”‹ A circuit is required for the experiment, consisting of a power supply, ammeter, wire, and voltmeter.
  • 🌑️ To avoid inaccuracies, the experiment should maintain a low current (below 1 amp) to prevent the wire from heating and changing its resistivity.
  • πŸ”© The length of the wire should be varied in controlled increments to observe how resistance changes, starting at a length that avoids shorting the circuit and excessive heating.
  • πŸ“ The diameter of the wire is measured in three places using a micrometer to find the mean, which is used to calculate the cross-sectional area.
  • πŸ“ˆ The experiment involves plotting resistance against length to obtain a straight line, with the gradient representing Rho / A.
  • πŸ” Uncertainties in the experiment arise from the resolution of the measuring instruments (voltmeter, ammeter, and micrometer) and must be accounted for in the results.
  • 🏹 To determine the percentage uncertainty in resistivity, both the percentage uncertainty in the area and the gradient must be considered.
  • 🎯 The final results should be compared to research values to validate the accuracy of the experiment.
  • πŸ“ The process involves recording PD (potential difference) across the wire and the current, then calculating resistance using Ohm's law (R = V / I).
Q & A

  • What is the main focus of the A-Level Physics practical investigation discussed in the transcript?

    -The main focus is to investigate how the resistance of a wire changes with its length and cross-sectional area, and to find the resistivity of the wire material.

  • What is the formula for resistivity mentioned in the transcript?

    -The formula for resistivity is given as Rhor (Rho) equals R times A over L, where R is resistance, A is the cross-sectional area, and L is the length of the wire.

  • Why is it important to maintain a low current during the experiment?

    -Maintaining a low current, below 1 amp, is important to avoid heating the wire, which could lead to inaccurate readings due to changes in resistivity with temperature.

  • How does the temperature affect the resistivity of the metal?

    -The resistivity of the metal can change with temperature. If the wire heats up, the resistivity may increase, leading to inaccurate experimental results.

  • What type of wire is recommended for this experiment?

    -A wire made of constantan is recommended because its resistivity does not change significantly with temperature, making it suitable for this type of experiment.

  • How is the length of the wire changed during the experiment?

    -The length of the wire can be changed either by physically cutting and reattaching it or by using a crocodile clip that can be moved along the wire to vary the length included in the circuit.

  • Where should the voltmeter be placed in the circuit to measure the potential difference (PD)?

    -The voltmeter should be placed across the wire to measure the PD across it. Alternatively, it could be placed across the entire circuit, as the PD would be the same.

  • How can the uncertainty in the experiment be minimized?

    -Uncertainty can be minimized by using the same gauge wire, ensuring the wire is taut to avoid parallax error, and keeping the current below 1 amp to prevent heating and changes in resistivity.

  • What is the method for calculating the cross-sectional area of the wire?

    -The cross-sectional area is calculated by measuring the diameter of the wire in three places using a micrometer and finding the mean, then using the formula area equals PI times (diameter squared) / 4.

  • How can the percentage uncertainty in resistivity be determined?

    -The percentage uncertainty in resistivity is determined by adding the percentage uncertainty in the area (which is twice the percentage uncertainty in the diameter) and the percentage uncertainty in the gradient of the length vs. resistance graph.

  • What is the final step in analyzing the results of the experiment?

    -The final step is to compare the calculated resistivity with a research value to check for accuracy, and to draw error bars and a line of worst fit on the graph to determine the percentage uncertainty in the gradient.

Outlines
00:00
πŸ”¬ Introduction to A-Level Physics Practical: Investigating Wire Resistance

This paragraph introduces an A-Level physics practical investigation focused on understanding how the resistance of a wire changes with its length and cross-sectional area. The goal is to determine the resistivity (Rho) of the wire, using the equation Rho equals R times A over L, where R is resistance, A is cross-sectional area, and L is length. The discussion includes the importance of setting up a circuit with a power supply, ammeter, and wire, and the considerations for changing wire length to observe resistance variations. It also touches on safety and accuracy, emphasizing the need to avoid overheating the wire and the importance of using low currents to maintain consistent resistivity throughout the experiment.

05:03
πŸ“ Measuring Wire Resistivity and Addressing Uncertainties

The second paragraph delves into the methodology of measuring the wire's resistivity by focusing on the cross-sectional area and the importance of accurate diameter measurements using a micrometer. It discusses the controls needed for a consistent experiment, such as using the same gauge wire and metal to minimize variability in resistivity due to temperature changes. The paragraph also addresses the concept of uncertainties in measurements, explaining how to calculate the percentage uncertainty in resistance by considering the resolution of the voltmeter, ammeter, and micrometer used. Additionally, it provides guidance on plotting the results and estimating the overall percentage uncertainty in resistivity, suggesting comparison with research values for validation.

Mindmap
Keywords
πŸ’‘Resistivity
Resistivity is a physical quantity that describes the ability of a material to conduct electricity. It is determined by the material's intrinsic properties and is independent of the object's shape or size. In the context of the video, resistivity (Rho) is calculated using the formula Rho = R * A / L, where R is the resistance, A is the cross-sectional area, and L is the length of the wire. The experiment aims to find the resistivity of the metal the wire is made of by changing its length and measuring the resulting resistance.
πŸ’‘Resistance
Resistance is the opposition that a material offers to the flow of electric current. It is directly proportional to the length of the conductor and inversely proportional to its cross-sectional area. In the video, resistance is the dependent variable that is measured to investigate how it changes with the length of the wire. The formula to calculate resistance is R = V / I, where V is the voltage (PD) across the wire and I is the current flowing through it.
πŸ’‘Circuit
A circuit is a path or interconnected network of electrical components through which an electric current can pass. In the video, a circuit is set up with a power supply (battery), an ammeter, a wire, and a voltmeter to measure the resistance and potential difference (voltage) across the wire. The circuit allows for the investigation of how resistance changes with the length of the wire.
πŸ’‘Potential Difference (PD)
Potential difference, also known as voltage, is the driving force that pushes electric charges through a conductor. It is the difference in electric potential between two points in a circuit. In the context of the video, PD is measured across the wire to determine the resistance. The script mentions that PD can be measured across the entire circuit or just across the wire itself.
πŸ’‘Ammeter
An ammeter is an instrument used to measure the current flowing through a circuit. In the video, an ammeter is included in the circuit to measure the current, which is a necessary value for calculating resistance. Keeping the current constant is crucial to ensure that the changes in resistance are solely due to changes in wire length.
πŸ’‘Voltmeter
A voltmeter is an instrument used to measure the potential difference, or voltage, between two points in a circuit. In the video, a voltmeter is used to measure the potential difference across the wire, which is necessary to calculate the resistance using Ohm's Law. Proper placement of the voltmeter is crucial to obtain accurate resistance measurements.
πŸ’‘Ohm's Law
Ohm's Law is a fundamental principle in electrical science that states that the current through a conductor between two points is directly proportional to the voltage across the two points and inversely proportional to the resistance between them. The law is usually expressed with the formula V = I * R, where V is the voltage, I is the current, and R is the resistance. In the video, Ohm's Law is used to calculate resistance by measuring voltage and current in the circuit.
πŸ’‘Micrometer
A micrometer is a precision measuring instrument used to measure very small distances, typically to an accuracy of micrometers (thousandths of a millimeter). In the video, a micrometer is used to measure the diameter of the wire in three places to find the mean diameter, which is then used to calculate the cross-sectional area for the resistivity experiment.
πŸ’‘Temperature
Temperature is a measure of the average kinetic energy of the particles in a substance and can affect the resistivity of materials. In the context of the video, it is important to maintain a constant temperature or use low currents to avoid changing the resistivity of the metal due to thermal effects. High temperatures can increase the resistivity of most conductors, which can lead to inaccurate experimental results.
πŸ’‘Uncertainty
Uncertainty in an experiment refers to the range of values within which the true value is believed to lie with a certain level of confidence. It arises from various sources such as measurement errors, environmental factors, and limitations of the equipment used. In the video, uncertainties in voltage, current, and wire diameter measurements contribute to the overall uncertainty in the calculated resistivity.
πŸ’‘Gradient
In the context of the video, the gradient refers to the slope of a graph, specifically the graph of resistance versus length of the wire. The gradient of this graph is equal to the resistivity of the wire divided by its cross-sectional area (Rho / A). By calculating the gradient, the resistivity of the metal can be determined, provided the cross-sectional area is known.
Highlights

Investigating the relationship between resistance of a wire and its length and cross-sectional area.

Using the resistivity equation, Rho equals R a over L, to find the resistivity of a wire.

Measuring resistance as the dependent variable in the experiment.

Exploring how changing the length of the wire affects its resistance.

The importance of a circuit setup with a power supply, ammeter, and wire for the experiment.

Avoiding short circuits by starting with a lengthier wire.

Considering the impact of temperature on resistivity and ensuring consistent current to avoid heating.

Using a crocodile clip to adjust the length of the wire in the circuit.

Positioning the voltmeter across the wire to measure potential difference (PD).

Calculating resistance using Ohm's law, R is V over I.

Recording PD across the wire and the current to calculate resistance.

Plotting resistance against length (L) to obtain a straight line and determine the gradient.

Understanding that the gradient of the graph equals Rho divided by a.

Measuring the wire's diameter in three places to find the mean and calculate the cross-sectional area.

Accounting for uncertainties in V, I, and the area to determine the percentage uncertainty in resistance.

Mitigating uncertainties by using the same gauge wire, low current, and ensuring the wire is taut.

Drawing a line of best fit and a line of worst fit to estimate the percentage uncertainty in the gradient.

Calculating the overall percentage uncertainty in resistivity by combining uncertainties in area and gradient.

Comparing the experimental value of resistivity with research values for accuracy.

Transcripts

Browse More Related Video

Resistivity - A-level Physics

A Level Physics: What is resistivity?

Resistivity and conductivity | Circuits | Physics | Khan Academy

2018 AP Physics 1 Free Response #2

Resistivity | Specific Resistance | Easier Explanation

Resistance of a Conductor | Electricity and Circuits | Don't Memorise

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsExperimentResistivityCalculationWirePropertiesElectricalCircuitsMeasurementTechniquesTemperatureEffectsDataAnalysisUncertaintyQuantificationEducationalContentScienceTutorial