High School Physics - Capacitors

Dan Fullerton
16 Dec 201106:23
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative talk, Mr. Fullerton introduces the concept of capacitors, focusing on parallel plate capacitors. He explains that capacitors consist of conductive plates separated by an insulator, capable of storing electrical charge. The talk delves into the formula for capacitance (C = Q/V), where C is capacitance in farads, Q is charge in coulombs, and V is voltage. Mr. Fullerton provides examples to demonstrate how to calculate capacitance and the charge on a capacitor's plates. He further discusses factors affecting capacitance, such as plate area, separation, and the permittivity of the dielectric material. The presentation concludes with a practical application of these concepts to determine the capacitance of specific scenarios and the distance between plates in an air-gap capacitor.

Takeaways
  • 📌 Capacitors are devices consisting of two conductive plates separated by an insulator, used to store electrical charge.
  • 🔋 The amount of charge stored per unit potential difference is known as capacitance, measured in farads (F).
  • 🔢 The formula for capacitance is C = Q / V, where C is the capacitance in farads, Q is the charge in coulombs, and V is the potential difference in volts.
  • 📈 The capacitance of a parallel plate capacitor depends on the area of the plates (A), the separation between them (d), and the permittivity of the dielectric material (ε).
  • 🌐 The permittivity of free space (ε₀) is a constant value of 8.854 × 10⁻¹² F/m.
  • 🔍 To find the capacitance of a capacitor, you can use the formula C = εA / d, where ε is the permittivity and A and d are the area and separation of the plates, respectively.
  • 💡 A larger plate area, smaller separation, and higher permittivity result in greater capacitance.
  • 🔧 Given a capacitance of 200 nF and a potential difference of 6V, the charge on the capacitor's plates can be calculated as Q = C × V = 200 × 10⁻⁹ F × 6V = 1.2 × 10⁻⁶ C.
  • 📏 For two parallel plates with dimensions of 1m by 1mm and 2mm separated by 3μm of air, the capacitance is approximately 5.9 pF.
  • 🔄 To find the separation between the plates of a capacitor, rearrange the capacitance formula to solve for d, giving d = εA / C.
  • 📚 For further study on capacitors, consider consulting physics resources and educational materials.
Q & A

  • What is the basic structure of a capacitor?

    -A capacitor consists of two conductive plates separated by an insulator, allowing it to store electrical charge.

  • What is the unit of capacitance?

    -The unit of capacitance is the farad (F), which is equivalent to a coulomb per volt (C/V).

  • What are some common units used to measure capacitance in electronic circuits?

    -Common units for capacitance include microfarads (µF), nanofarads (nF), and picofarads (pF).

  • How is the capacitance of a parallel plate capacitor calculated?

    -The capacitance (C) of a parallel plate capacitor is calculated using the formula C = εA/D, where ε is the permittivity of the dielectric material, A is the area of the plates, and D is the separation between the plates.

  • What is the permittivity of free space, and what is its value?

    -The permittivity of free space, denoted by ε₀, is a constant that represents the permittivity of vacuum and air. Its value is approximately 8.854 × 10⁻¹² F/m (farads per meter).

  • How does the area of the plates in a capacitor affect its capacitance?

    -A larger plate area increases the capacitance of the capacitor, as it allows for more charge to be stored for the same potential difference.

  • How does the separation between the plates of a capacitor influence its capacitance?

    -The closer the plates are to each other, the greater the capacitance, because the electric field is stronger and more charge can be stored for the same potential difference.

  • What is the relationship between the permittivity of the dielectric material and the capacitance of a capacitor?

    -A higher permittivity of the dielectric material results in greater capacitance, as it enhances the ability of the capacitor to store charge within the electric field.

  • Given a 200 nanofarad capacitor charged to a potential difference of 6 volts, how much charge is on the top plate?

    -The charge (Q) on the top plate can be calculated using the formula Q = C × V. For a 200 nF capacitor charged to 6 volts, Q = 200 × 10⁻⁹ F × 6 V = 1.2 × 10⁻⁶ C or 1.2 µC (microcoulombs).

  • If two parallel plates have an area of 0.001 m² and are separated by 3 micrometers, what is the capacitance if the dielectric is air?

    -Using the formula C = ε₀A/D, with ε₀ = 8.854 × 10⁻¹² F/m, A = 0.001 m², and D = 3 × 10⁻⁶ m, the capacitance is C = 8.854 × 10⁻¹² F/m × 0.001 m² / (3 × 10⁻⁶ m) = 5.9 × 10⁻¹² F or 5.9 pF (picofarads).

  • For a capacitor with a capacitance of 5 nanofarads and plate area of 0.06 m², what is the distance between the plates?

    -Using the formula D = ε₀A/C and solving for D, with ε₀ = 8.854 × 10⁻¹² F/m, A = 0.06 m², and C = 5 × 10⁻⁹ F, the distance is D = (8.854 × 10⁻¹² F/m × 0.06 m²) / (5 × 10⁻⁹ F) = 1.1 × 10⁻⁴ m or 11 µm.

Outlines
00:00
🔋 Understanding Capacitors and Capacitance

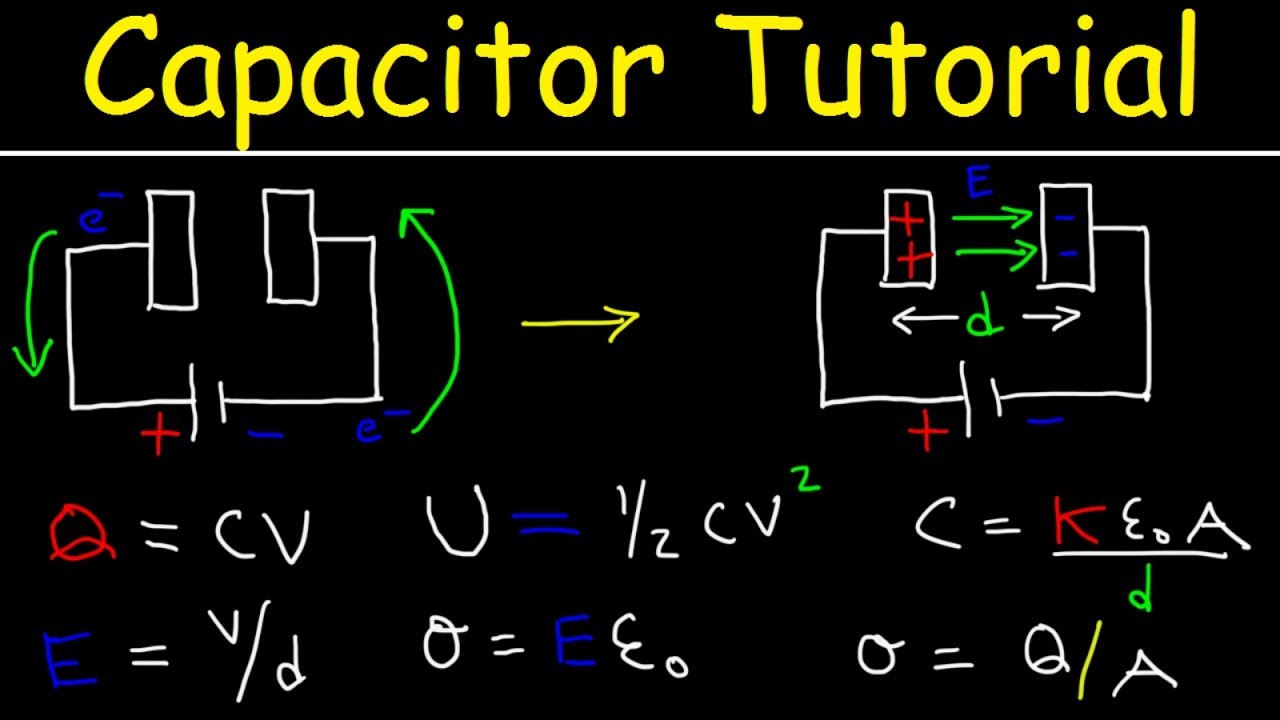
This paragraph introduces the concept of capacitors, specifically focusing on parallel plate capacitors. It explains that capacitors consist of conductive plates separated by an insulator, capable of storing electrical charge. The definition of capacitance is provided, which is the amount of charge stored per unit potential difference, measured in farads. The paragraph further elaborates on the formula for capacitance (C = Q/V), where Q is the charge in coulombs and V is the potential difference in volts. Two examples are worked out to demonstrate how to calculate capacitance and the charge on a capacitor's plates given certain conditions. The factors affecting capacitance, such as plate area, separation, and the permittivity of the dielectric material, are also discussed, with a formula provided for calculating capacitance based on these factors (C = εA/D).

05:03
📏 Calculating Plate Separation and Capacitance

The second paragraph continues the discussion on capacitors, focusing on the calculation of the distance between plates in a capacitor and the capacitance itself. It starts by explaining the formula for finding the separation between plates (D = εA/C) and uses this formula to calculate the distance in a 5 nanofarad air gap capacitor with a plate area of 0.06 square meters. The permittivity of free space (ε₀) is introduced, with its value and units provided. The paragraph then guides the listener through the process of calculating the capacitance of two parallel plates with given dimensions and separation, using the permittivity of air (ε₀). The example calculation helps to illustrate the relationship between the physical properties of the capacitor and its capacitance.

Mindmap
Keywords
💡Capacitors
Capacitors are electronic components that store electrical charge. In the context of the video, they consist of two conductive plates separated by an insulator (dielectric). The ability of a capacitor to store charge is measured by its capacitance. The script explains that capacitors can store more electrical charge as their capacitance increases, which is directly related to the size of the plates, the distance between them, and the permittivity of the dielectric material used.
💡Capacitance
Capacitance is a measure of a capacitor's ability to store electrical charge per unit potential difference. It is expressed in farads (F), with common units including microfarads (μF) and picofarads (pF). The capacitance of a parallel plate capacitor can be calculated using the formula C = εA/D, where ε is the permittivity of the dielectric, A is the area of the plates, and D is the separation between the plates. The video emphasizes that higher capacitance values allow for more charge storage at the same potential difference.
💡Parallel Plate Capacitors
A parallel plate capacitor is the simplest type of capacitor, consisting of two parallel conductive plates separated by an insulating material or dielectric. The script explains that the capacitance of such a capacitor depends on the area of the plates, the distance between them, and the permittivity of the dielectric. The larger the area, the closer the plates, and the higher the permittivity, the greater the capacitance of the parallel plate capacitor.
💡Insulator (Dielectric)
An insulator, referred to as a dielectric in the context of capacitors, is a material that separates the conductive plates and prevents the flow of electric current, while still allowing for the storage of electrical charge. The dielectric's properties affect the capacitor's capacitance. The script mentions that the permittivity of the dielectric, denoted by the Greek letter ε (epsilon), is a measure of how well the insulator can store charge in an electric field. The permittivity of free space, or vacuum, is given the symbol ε0 and is a constant value used in capacitance calculations.
💡Electrical Permittivity (Epsilon)
Electrical permittivity, symbolized by the Greek letter ε (epsilon), is a measure of a material's ability to store electrical charge in an electric field. It is a property of the dielectric material used in capacitors. The permittivity of free space, ε0, is a fundamental constant used as a reference. The script explains that the capacitance of a capacitor can be calculated using the formula C = εA/D, where ε is the permittivity of the dielectric, A is the area of the plates, and D is the separation between the plates.
💡Charge (Q)
Electrical charge (Q) is a fundamental property of matter that constitutes the basis for electric charge storage in capacitors. The script discusses how the amount of charge a capacitor can store is directly related to its capacitance. The unit of charge is the coulomb (C), and the script provides examples of calculating capacitance using the charge stored on the plates of a capacitor.
💡Potential Difference (Voltage)
Potential difference, commonly known as voltage, is the measure of the electric potential between two points. In the context of capacitors, it is the voltage across the plates that allows for charge storage. The script explains that the capacitance of a capacitor is directly proportional to the amount of charge it stores and inversely proportional to the potential difference. Voltage is measured in volts (V), and the script uses this concept to solve for charge and capacitance in different scenarios.
💡Farad (F)
The farad (F) is the SI unit of capacitance, representing the amount of charge in coulombs that a capacitor can store at a potential difference of one volt. Although a farad is a very large unit, the script discusses smaller units like microfarads (μF) and picofarads (pF) which are commonly used in practice. The farad is defined as a coulomb per volt, and the script uses this unit to calculate and express capacitance values.
💡Coaxial Cable
Although the term 'Coaxial Cable' is not explicitly mentioned in the script, it is a related concept worth noting. A coaxial cable is a type of cable that has a central conductor, surrounded by a dielectric insulator, a braided shield, and an outer insulating jacket. It is designed to maintain signal integrity by reducing electromagnetic interference. Coaxial cables can be thought of as a type of capacitor where the central conductor and the shield act as the plates, and the dielectric material between them serves as the insulator.
💡 Coulomb (C)
The coulomb (C) is the SI unit of electric charge. It is the amount of charge transferred by a steady current of one ampere in one second. In the context of the script, coulombs are used to quantify the electrical charge stored in a capacitor. The script discusses how the capacitance of a capacitor is calculated using the amount of charge in coulombs and the potential difference in volts.
💡Ohm's Law
Ohm's Law, while not directly mentioned in the script, is a fundamental principle in electrical engineering that relates voltage (V), current (I), and resistance (R). It states that the voltage across a conductor is directly proportional to the current through it, with the proportionality constant being the resistance. Although the law itself is not discussed, the concept of potential difference (voltage) is central to understanding capacitance and charge storage in capacitors, as Ohm's Law helps to describe the relationship between these electrical quantities.
💡Physics Comm
Physics Comm is mentioned in the script as a resource for additional help and information on the topic of capacitors. It likely refers to a community or platform where individuals can seek further explanations, ask questions, and engage in discussions about physics concepts, including those related to capacitors and their properties.
Highlights

Capacitors are devices that store electrical charge and can be used to solve basic problems in electrical circuits.

A parallel plate capacitor consists of two conductive plates separated by an insulator (dielectric).

Capacitance is the amount of charge that can be stored per unit potential difference and is measured in farads.

The formula for capacitance is C = Q/V, where C is the capacitance in farads, Q is the charge in coulombs, and V is the potential difference in volts.

A capacitor can store more electrical charge as its capacitance increases, for the same potential difference.

Capacitors are typically used in smaller units such as microfarads, nanofarads, and picofarads due to the large size of a farad.

To find the capacitance of a capacitor given the charge and potential difference, use the formula C = Q/V.

To find the charge on the plates of a capacitor given its capacitance and potential difference, rearrange the formula to Q = C * V.

The capacitance of a capacitor is directly proportional to the area of the plates and the permittivity of the dielectric material.

The capacitance is inversely proportional to the separation between the plates.

The permittivity of a dielectric material, denoted by epsilon (ε), measures how well the material can store charge in an electric field.

The permittivity of free space (vacuum and air) is a constant, denoted by ε₀, and is equal to 8.854 × 10^-12 F/m.

The capacitance of two parallel plates can be calculated using the formula C = εA/D, where A is the area of the plates and D is the separation between them.

To find the separation between the plates of a capacitor, rearrange the capacitance formula to D = εA/C.

The capacitance of a capacitor can be affected by the area of the plates, the distance between the plates, and the permittivity of the dielectric material.

By understanding the principles of capacitance, one can solve for various parameters in electrical circuits involving capacitors.

Capacitors have a wide range of applications in electronic devices and systems, from energy storage to signal filtering.

For further study on capacitors and their applications, one can refer to physics and electronics resources.

Transcripts

Browse More Related Video

Capacitors - Basic Introduction - Physics

Dielectrics in capacitors | Circuits | Physics | Khan Academy

Capacitance | Circuits | Physics | Khan Academy

Electric Permittivity

Resistors and Capacitors

Electric Field of Parallel Plates

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Capacitor BasicsPhysics EducationElectrical EngineeringParallel PlateCapacitance FormulaDielectric MaterialsElectric ChargePotential DifferenceElectromagnetismTechnical Tutorial