Capacitance | Circuits | Physics | Khan Academy

Khan Academy
23 May 200813:34
EducationalLearning
32 Likes 10 Comments

TLDRThis educational script explores the concept of an infinite uniformly charged plane and its electric field properties, transitioning to the behavior of finite charged plates. It explains how the electric field between two oppositely charged parallel plates combines to create a constant field near the center, leading to a discussion on voltage and its relationship with charge. The script derives the formula for voltage across a capacitor, introducing the concept of capacitance and permittivity of free space, laying the groundwork for understanding electrical pressure and the flow of charge.

Takeaways
  • 🌟 The electric field generated by an infinite uniformly charged plane is constant and perpendicular to the plane.
  • πŸ” Charge density is defined as the total amount of charge divided by the area, and it's difficult to work with for an infinite plane due to infinite area leading to infinite charge density.
  • πŸ“š For a finite plane with a non-zero area, the electric field near the center approximates that of an infinite uniformly charged plane.
  • πŸ”‹ When two oppositely charged parallel plates are close to each other, the electric field between them is the sum of the individual fields, being constant near the center.
  • πŸ”„ The total electric field between two charged plates is additive and can be calculated as 4K pi times the charge density (Q/A).
  • ⚑ The voltage difference between two points is the electrical potential energy per unit charge, representing how much 'pressure' there is for a charge to move from one point to another.
  • πŸ”Œ The voltage across a pair of charged plates is directly proportional to the charge on the plates and inversely proportional to the distance between them, with the area of the plates being a constant factor.
  • βš–οΈ Capacitance (measured in Farads) is the ratio of the charge on the plates to the voltage across them and is determined by the configuration of the plates (area and distance).
  • πŸ“ The permittivity of free space (epsilon nought) is a constant that relates capacitance to the physical properties of the space between the plates.
  • πŸ”„ Understanding the relationship between charge, voltage, and capacitance is fundamental to grasping the behavior of capacitors in electrical circuits.
  • πŸ›  The script emphasizes the importance of intuitive understanding of voltage as a key concept in electrical engineering.
Q & A

  • What is the electric field generated by an infinite uniformly charged plane?

    -The electric field generated by an infinite uniformly charged plane is constant in magnitude and direction, with field lines of equal size.

  • How is the strength of the electric field related to the charge density of the plate?

    -The strength of the electric field is equal to 2 times Coulomb's constant times pi times the charge density of the plate, which is the total charge divided by the area.

  • Why is it difficult to work with an infinite plane when calculating charge density?

    -The area of an infinite plane is infinite, and since charge density is charge per area, both the charge and the charge density would also be infinite, making calculations impractical.

  • What is the concept of charge density in the context of the script?

    -Charge density is the total amount of charge divided by the area, representing the charge per unit area on the plane.

  • How does the electric field between two parallel plates compare to that of a single plate?

    -The electric field between two parallel plates is essentially the sum of the electric fields generated by each plate, with the fields being additive and constant near the center if the plates are close together.

  • What is the relationship between the electric field and the voltage difference across two plates?

    -The voltage difference between two plates is directly proportional to the electric field and the distance between the plates, as the voltage difference is the work done per unit charge against the electric field over the distance.

  • How is the total electric field between two charged plates calculated?

    -The total electric field between two charged plates is calculated by adding the electric fields generated by each plate, which is 4K pi times the charge density (Q/A) if both plates have the same area and are close together.

  • What is the significance of the term 'capacitance' in the context of this script?

    -Capacitance is a measure of a system's ability to store electrical charge, and it is directly proportional to the charge on the plates and inversely proportional to the voltage across them, given a fixed configuration.

  • What is the permittivity of free space, and how does it relate to capacitance?

    -The permittivity of free space, often denoted as epsilon nought, is a constant that relates the charge and voltage in a system. It is part of the formula for capacitance when considering the area of the plates and the distance between them.

  • How does the voltage across a capacitor relate to the charge stored in it?

    -The voltage across a capacitor is directly proportional to the charge stored in it. For a given configuration (fixed area and distance), knowing the charge allows you to calculate the voltage, and vice versa.

  • What is the unit of capacitance, and what does it signify?

    -The unit of capacitance is the Farad. It signifies the amount of charge in coulombs that a capacitor can store for every volt of potential difference across its plates.

Outlines
00:00
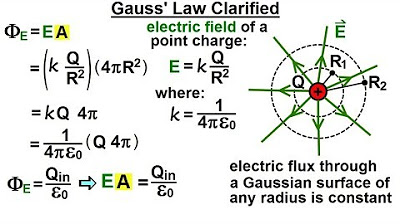
πŸ”‹ Understanding Infinite Uniformly Charged Planes and Electric Fields

This paragraph introduces the concept of an infinite uniformly charged plane, explaining that the electric field it generates is constant in strength and direction. The field lines are depicted as equally spaced, indicating uniformity. The strength of the electric field is derived from Coulomb's constant, charge density, and the properties of the plane. Charge density is defined as the total charge per unit area, and the challenge of working with an infinite plane is discussed due to the infinite area leading to infinite charge density. The paragraph also touches on the approximation of an infinite plane by a finite plane for the purpose of calculating electric fields near its center.

05:03
πŸ”Œ Calculating Electric Field and Voltage in a Capacitor Configuration

The second paragraph delves into the electric field and voltage calculations for a pair of parallel plates with equal but opposite charges, simulating a capacitor. It explains that the electric field between the plates is the sum of the fields from each plate, which are constant near the center if the distance between the plates is not too large. The voltage difference between two points is reviewed, relating it to the electrical potential energy per charge. The work done against the electric field to move a charge is calculated, leading to the formula for voltage difference in terms of the electric field and the distance between the plates. The relationship between charge, electric field, and voltage is established, highlighting the additive nature of electric fields from oppositely charged plates.

10:03
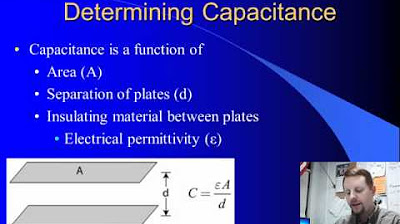
πŸ”„ The Relationship Between Voltage, Charge, and Capacitance in Capacitors

The final paragraph explores the relationship between voltage, charge, and a property called capacitance in the context of a capacitor. It provides a formula that directly relates the charge on the plates to the voltage across them, factoring in the area of the plates and the distance between them. The concept of capacitance is introduced as a measure of a system's ability to store charge per unit voltage, with its unit being the Farad. The permittivity of free space, denoted by epsilon nought, is mentioned as a constant in the equations. The paragraph concludes by emphasizing the direct proportionality between voltage and charge for a given capacitor configuration, and the importance of understanding capacitance in electrical engineering.

Mindmap
Keywords
πŸ’‘Infinite Uniformly Charged Plane
An infinite uniformly charged plane refers to a theoretical construct in physics where a plane extends infinitely in two dimensions and has a uniform distribution of electric charge across it. In the video, this concept is used to discuss the generation of a constant electric field, which is a fundamental concept in understanding the behavior of electric fields and their influence on charged particles.
πŸ’‘Electric Field
The electric field is a vector field that surrounds electrically charged particles and exerts force on other charged particles within the field. In the context of the video, the electric field is depicted as being generated by a uniformly charged plane and is visualized through field lines, which are indicative of the field's strength and direction.
πŸ’‘Charge Density
Charge density is defined as the amount of electric charge per unit area (or volume, in three dimensions). In the script, charge density is used to calculate the strength of the electric field generated by the charged plane, highlighting its importance in determining the field's properties.
πŸ’‘Coulomb's Constant
Coulomb's constant, denoted as 'K' in the script, is a fundamental physical constant that appears in the formula for the electric force between two point charges. It is used in the video to relate the charge density of the plane to the strength of the electric field it generates.
πŸ’‘Voltage
Voltage, often referred to as electric potential difference, is the work needed per unit of charge to move a test charge between two points. In the video, voltage is discussed in terms of the potential energy difference across two charged plates and is key to understanding the relationship between charge and electric potential.
πŸ’‘Parallel Plates
Parallel plates refer to two flat surfaces that are parallel to each other and are often used in physics to model capacitors. In the script, the concept of parallel plates is used to explore the electric field and voltage between two charged surfaces and to introduce the concept of capacitance.
πŸ’‘Capacitance
Capacitance is a measure of a system's ability to store electrical charge. It is defined as the ratio of the charge on one plate of a capacitor to the potential difference between the plates. The video explains how capacitance is derived from the geometry and charge distribution of the system, highlighting its importance in electrical engineering.
πŸ’‘Electric Potential Energy
Electric potential energy is the work that has been done to move a charge against an electric field. In the video, it is used to describe the energy required to move a charge between two points in an electric field, which is directly related to the concept of voltage.
πŸ’‘Permittivity of Free Space
The permittivity of free space, often denoted as 'epsilon nought' in the script, is a physical constant that relates to the ability of a vacuum to permit electric fields. It is a fundamental concept in the video's discussion of capacitance and the calculation of electric fields.
πŸ’‘Farad
The Farad is the unit of capacitance in the International System of Units (SI). It is named after the scientist Michael Faraday and is used in the video to quantify the capacity of a system to store electrical charge, as discussed in the context of the parallel plates.
πŸ’‘Electron Flow
Electron flow refers to the movement of electrons, which are negatively charged particles, within a conductor. Although not explicitly detailed in the script, the concept is alluded to when discussing the movement of charge in response to an electric field, which is a fundamental aspect of electric current and circuits.
Highlights

An infinite uniformly charged plane generates a constant electric field.

Electric field strength is calculated as 2 times Coulomb's constant times pi times the charge density of the plate.

Charge density is defined as the total amount of charge divided by the area.

The concept of a non-infinite plane approximating an infinite uniformly charged plane near its center is introduced.

Two parallel plates with equal and opposite charges create a constant electric field between them near the center.

The electric field generated by each plate is additive, resulting in a total electric field of 4K pi times charge per area (Q/A).

Voltage difference is defined as the electrical potential energy per charge.

The work necessary to move a charge against an electric field is calculated as force times distance.

Voltage is likened to electrical pressure, indicating how much a charge wants to move from one point to another.

The relationship between the voltage difference and the electric field is established as the product of the electric field and distance.

A formula for voltage difference in terms of the electric field, charge, area, and distance is derived.

The concept of capacitance is introduced, showing a direct proportionality between voltage and charge for a given configuration.

The term 1/(4K pi) is identified as the permittivity of free space or vacuum, a fundamental constant in electrical calculations.

The relationship between charge, voltage, and capacitance is expressed as Q = C * V, where C is the capacitance.

Capacitance is defined for a given configuration of plates and is measured in Farads.

The video concludes with an overview of how voltage can be calculated across a capacitor and the significance of capacitance in electrical engineering.

Transcripts

Browse More Related Video

Gauss Law Problems - Infinite Sheet of Charge and Parallel Plate Capacitor - Physics

Electric Field of Parallel Plates

Electric Flux and Gauss' Law - Review for AP Physics C: Electricity and Magnetism

High School Physics - Capacitors

Electric Fields: Crash Course Physics #26

Physics 37.1 Gauss's Law Understood (4 of 29) Gauss' Law Clarified

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Electric FieldsVoltage BasicsCharge DensityCapacitanceCoulomb's LawUniform ChargeElectric PotentialParallel PlatesElectrical EngineeringPhysics Education