Hydrostatic Force Problems - Calculus 2
TLDRThe video script discusses the calculation of hydrostatic force on submerged vertical plates of various shapes, including square, triangular, trapezoidal, and semicircular plates. It explains the process of determining the weight density of water, setting up the integral for hydrostatic force, and calculating the force for each shape. The script emphasizes understanding the relationship between depth (y), length (l), and the water's weight density, and provides a clear methodology for calculating hydrostatic forces using integral calculus.
Takeaways
- 📐 The hydrostatic force on a submerged object can be calculated using the formula involving the weight density of the fluid, the depth of the submerged area, and the area itself.
- 🌊 For a square vertical plate submerged in water, the hydrostatic force is determined by integrating the weight density times the depth over the length of the plate from its top to bottom edges.
- 📈 The weight density of water is 9,800 newtons per cubic meter when using the metric system, and 62.4 pounds per cubic foot when using the imperial system.
- 🔢 The anti-derivative of the depth function (h(y)) is used to evaluate the integral to find the hydrostatic force on the submerged object.
- 🏠 For a triangular plate, the hydrostatic force is calculated by integrating the product of the weight density, the function for the length along the y-axis (l(y)), and the depth function (h(y)) from the bottom to the top of the plate.
- 📉 The slope of the function for the length of the plate (l(y)) is determined by the change in length divided by the change in depth, and the y-intercept is found using a known point on the function.
- 🤔 For a trapezoidal plate, the hydrostatic force is calculated by integrating the product of the weight density, the function for the length along the y-axis (l(y)), and the depth function (h(y)) from the bottom to the top edge of the trapezoid.
- 🏢 The function for the length of the trapezoidal plate (l(y)) is a linear equation derived from the dimensions of the top and bottom bases and the height of the trapezoid.
- 🌐 For a semi-circular plate, the hydrostatic force is calculated by integrating the product of the weight density, the function for the length along the y-axis (l(y)), and the depth function (h(y)) across the semi-circle.
- 📏 The function for the length of the semi-circular plate (l(y)) is derived from the equation of a circle and is a function of y that represents the distance from the y-axis to the edge of the semi-circle at a given depth.
- 🔍 Understanding the concept of pressure and weight force is crucial when dealing with hydrostatic forces, as pressure is the force per unit area and weight force is the product of mass and gravity.
Q & A
What is the hydrostatic force on a vertical square plate submerged in water?
-The hydrostatic force on the vertical square plate submerged in water is calculated using the formula involving the weight density of water, the integral of the depth along the y-axis, the length of the plate along the x-axis, and the differential area element. In the given example, with the water density of 9800 N/m³, the plate 2 meters below the surface and with a side length of 2 meters, the force is determined to be 117,600 N.
How do you determine the values of c and d in the integral for calculating hydrostatic force?
-The values of c and d in the integral are determined by the depth of the submerged object. For the square plate example, c is -4 meters (the depth of the bottom of the plate) and d is -2 meters (the depth of the top of the plate). The integral is then evaluated from c to d along the y-axis.
What is the weight density of water in different units?
-The weight density of water is 9800 N/m³ when using metric units (meters, cubic meters), and it is 62.4 lb/ft³ when using imperial units (feet, cubic feet).
How do you calculate the hydrostatic force on a triangular plate submerged in water?
-The hydrostatic force on a triangular plate submerged in water is calculated by first determining the depth function h(y) as -y, then finding the points c and d along the y-axis that correspond to the depth of the plate, and finally integrating the product of the weight density of water, the function for the length along the x-axis l(y), the depth function h(y), and the differential area element dy from c to d.
What is the function for l(y) for a triangular plate submerged in water?
-The function for l(y) for a triangular plate is derived from the geometry of the triangle. It is a linear function with a slope of -2/3 and a y-intercept (l intercept) of -2, so l(y) = -2/3 * y - 2.
How do you calculate the hydrostatic force on a trapezoidal plate submerged in water?
-Similar to other shapes, the hydrostatic force on a trapezoidal plate is calculated by determining the depth function h(y) as -y, finding the left side function l(y) based on the dimensions of the trapezoid, and then integrating the product of the weight density of water, l(y), h(y), and dy from the depth of the top base to the depth of the bottom base.
What is the function for l(y) of a trapezoidal plate submerged in water?
-The function for l(y) of a trapezoidal plate is a linear function with a slope of 1 (since the change in length l is equal to the change in depth y) and a y-intercept of 12 (when y is 0, l is 12), so l(y) = y + 12.
How do you calculate the hydrostatic force on a semicircular plate submerged in water?
-The hydrostatic force on a semicircular plate is calculated by setting up the integral with the appropriate limits, the weight density of water, the function for the length along the x-axis l(y) derived from the geometry of the semicircle (l(y) = 2 * sqrt(100 - y²)), and the depth function h(y) as -y.
What is the relationship between pressure and weight density in fluid mechanics?
-Pressure is defined as force divided by area, while weight density is the weight force divided by volume. The weight force is mass times gravitational acceleration (mg), and weight density (ρ) is the mass per unit volume times gravitational acceleration (g). Therefore, pressure and weight density are related but distinct properties used in fluid mechanics.
How can you convert the weight density of water from newtons per cubic meter to pounds per cubic foot?
-To convert the weight density of water from newtons per cubic meter (N/m³) to pounds per cubic foot (lb/ft³), you first need to convert the mass unit from kilograms to pounds and the length unit from meters to feet. Multiply the density in kilograms per cubic meter (kg/m³) by the conversion factor for kilograms to pounds (2.20462) and raise the conversion factor for meters to feet (3.28084 ft/m) to the third power, then divide by this value to get the weight density in lb/ft³. The resulting weight density of water is approximately 62.4 lb/ft³.
What is the significance of understanding the weight density of water in engineering calculations?
-Understanding the weight density of water is crucial in engineering calculations as it allows for accurate determination of forces, such as hydrostatic force, acting on submerged structures. It is essential for designing and analyzing the stability and structural integrity of underwater constructions, like dams, pipelines, and marine platforms.
How does the shape of a submerged object affect the calculation of hydrostatic force?
-The shape of a submerged object significantly affects the calculation of hydrostatic force because it determines how the depth (h(y)) and the length or width (l(y)) vary along the object's surface. Different shapes require different mathematical functions to describe these variations, leading to different integral expressions for calculating the hydrostatic force.
Outlines
🌊 Hydrostatic Force on a Submerged Square Plate
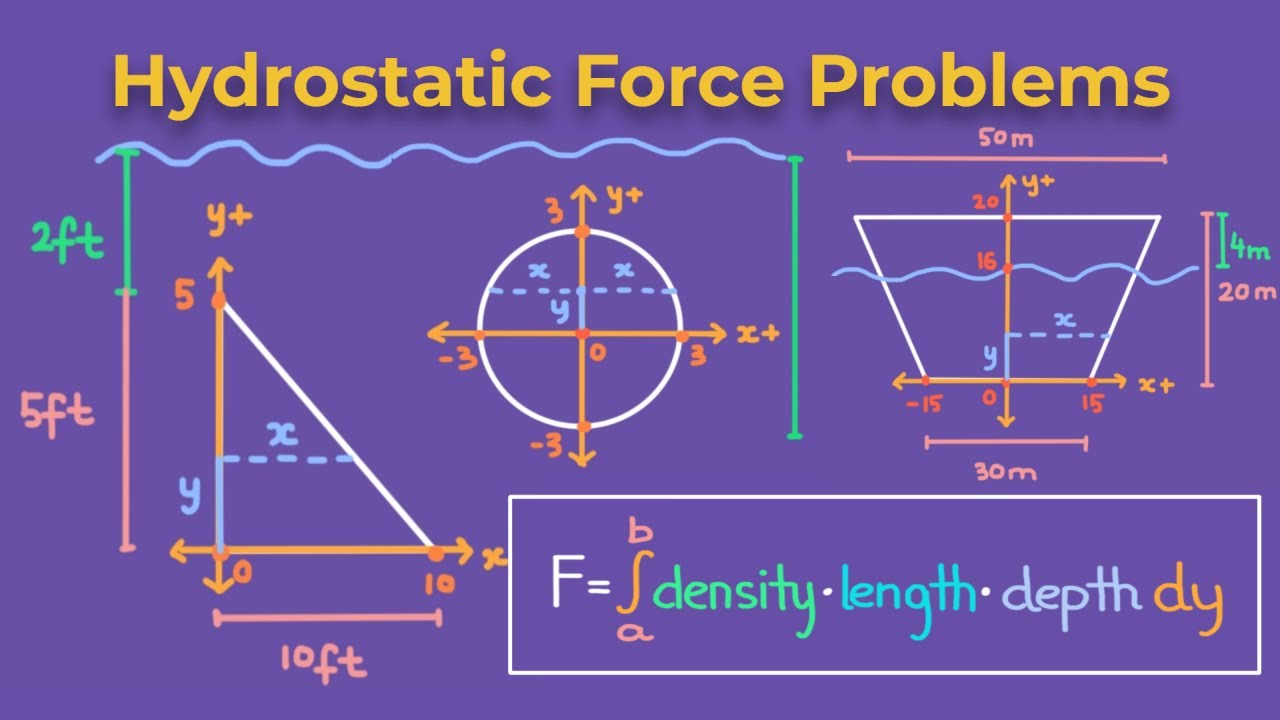
This paragraph discusses the calculation of hydrostatic force on a square vertical plate submerged in water. The plate is 2 meters below the surface with a side length of 2 meters. The explanation begins by establishing the x and y axes, with the water level as the x-axis and the y-axis perpendicular to it. The formula for hydrostatic force is given as the weight density of water multiplied by the integral from c to d along the y-axis of h(y) times l(y), with h(y) representing the depth of water below the surface and l(y) the length of the plate along the x direction. The weight density of water is 9,800 newtons per cubic meter when using meters, and the depth and length of the plate are used to determine the constants c and d for integration. The integral is evaluated from negative four to negative two, resulting in a force of 117,600 newtons.
📐 Hydrostatic Force on a Submerged Triangular Plate
The second paragraph focuses on calculating the hydrostatic force on a triangular vertical plate submerged in water, situated 3 meters below the surface with sides of 9 meters and 6 meters. The process involves determining h(y) as negative y and identifying the constants c and d for integration, which are -12 and -3, respectively. The weight density of water is again 9,800 newtons per cubic meter. A function for l(y), representing the length along the x direction, is derived using the slope of the plate sides. The final formula for hydrostatic force includes the weight density, the definite integral from c to d, and the function for l(y) and h(y). The integral results in a hydrostatic force of 2,381,400 newtons.
🔺 Hydrostatic Force on a Submerged Trapezoidal Plate
This paragraph describes the process of calculating the hydrostatic force on a trapezoidal plate submerged just below the water surface with dimensions of 12 feet on the top side, 20 feet on the bottom base, and 8 feet in height. The x and y axes are defined, with h(y) being negative y. The constants for integration, c and d, are determined to be -8 and 0, respectively. A function for l(y), the length along the x direction, is derived from the change in l over the change in y, resulting in a slope of 1 and a y-intercept of 12. The weight density of water is given in pounds per cubic foot (62.4) due to the use of feet as the unit. The final calculation, incorporating the weight density, the definite integral, and the functions for l(y) and h(y), yields a hydrostatic force of 34,611 pounds.
🌙 Hydrostatic Force on a Submerged Semi-Circular Plate
The fourth paragraph details the computation of hydrostatic force on a semi-circular plate with a 20-meter diameter submerged in water. The weight density is 9,800 newtons per cubic meter, and h(y) is negative y. The challenge lies in expressing the length l(y) as a function of y rather than x, which is achieved by relating the semicircle to a circle and using the equation x^2 + y^2 = r^2. The function for l(y) is derived as 2 times the square root of (100 - y^2). The hydrostatic force is calculated using the weight density, the definite integral from c to d, and the functions for l(y) and h(y), resulting in a force of 6,530,333 newtons.
📚 Understanding Weight Density and Pressure
The final paragraph provides an educational overview of weight density and pressure in the context of water on a surface. It clarifies that pressure is defined as force divided by area, and the weight force (mg) is different from weight density, which is the weight force divided by volume. The weight density is calculated as the density of water (1000 kg/m^3) times gravitational acceleration (9.8 m/s^2), resulting in 9,800 newtons per cubic meter. The explanation continues with a method to convert the weight density into pounds per cubic feet, using the conversions for kilograms to pounds and meters to feet, ultimately resulting in 62.4 pounds per cubic feet.
Mindmap
Keywords
💡Hydrostatic Force
💡Weight Density
💡Integral
💡Fluid Mechanics
💡Pressure
💡Depth
💡Semicircle
💡Trapezoid
💡Right Triangle
💡Square Plate
💡Negative Sign
Highlights
The concept of hydrostatic force and its calculation on submerged vertical plates is discussed.
A square plate submerged 2 meters below the surface of the water with a side length of 2 meters is used as an example to explain the calculation.
The importance of determining the x and y axes for the calculation of hydrostatic force is emphasized.
The formula for hydrostatic force is given, involving the weight density of water and an integral along the y-axis.
The weight density of water is 9,800 newtons per cubic meter when using meters, and 62.4 pounds per cubic foot when using feet.
The process of calculating the hydrostatic force on the square plate is detailed, including the determination of the limits of integration and the anti-derivative.
The final answer for the square plate is 117,600 newtons, representing the hydrostatic force.
A triangular plate submerged 3 meters below the water surface with a height of 9 meters and a base of 6 meters is used as the next example.
The method for determining the function for l of y (length along the x direction) based on the depth is explained.
The calculation of the hydrostatic force on the triangular plate results in 2,381,400 newtons.
A trapezoidal plate just below the water surface with dimensions of 12 feet on the top side, 20 feet on the bottom base, and 8 feet in height is the subject of another problem.
The method for calculating the hydrostatic force on the trapezoidal plate is described, including the determination of the slope and the function for l of y.
The final result for the trapezoidal plate is 34,611 pounds, showcasing the application of the hydrostatic force formula.
A semi-circle with a 20-meter diameter is the final example, and the hydrostatic force acting on it is calculated.
The method for determining l of y for the semi-circle involves the equation of a circle and the relationship between x and y.
The calculated hydrostatic force on the semi-circular plate is six million, five hundred thirty thousand, 333 newtons.
The concept of pressure is introduced, defined as force divided by area, and distinguished from weight force and weight density.
The weight density of water is further explained, including its derivation from the density of water and gravitational acceleration.
The units of weight density are clarified, with 9,800 newtons per cubic meter in metric units and 62.4 pounds per cubic foot in imperial units.
Transcripts
Browse More Related Video
Hydrostatic Force Problems - Calculus 2

Sect 8 3 #6 Hydrostatic Force, Calculus 2
Calculating the Work Required to Drain a Tank
calculating work, pumping water out of a rectangular tank, calculus 2 tutorial
calculating work by using integral, pumping water out of a tank, calculus 2 tutorial

20. Fluid Dynamics and Statics and Bernoulli's Equation
5.0 / 5 (0 votes)
Thanks for rating: