Hydrostatic Force Problems - Calculus 2
TLDRThis educational video script outlines the process of calculating hydrostatic force on submerged objects of various shapes, including rectangles, triangles, trapezoids, and circles. It explains the importance of understanding dimensions, density, and the integral formula for hydrostatic force. The script provides step-by-step instructions on setting up integrals, converting variables, and applying mathematical theorems to simplify calculations, ultimately yielding the force in Newtons or pounds depending on the units used.
Takeaways
- 📚 The script explains how to calculate hydrostatic force on submerged objects with different shapes: rectangles, triangles, trapezoids, and circles.
- 📏 For a rectangular object, the hydrostatic force is calculated using an integral formula that considers the density of water, the dimensions of the rectangle, and the depth of submersion.
- 📐 The script provides a step-by-step method to determine the parameters needed for the integral formula, including converting the length of a stripe into terms of the variable y.
- 🌡 The density of water is given as 62.5 pounds per cubic foot in imperial units and 9800 Newtons per cubic meter in metric units.
- 🏳️🌈 The concept of hydrostatic force involves breaking down the submerged surface into thin stripes and calculating the force on each stripe, then summing these forces.
- 🔍 The script uses the example of a submerged rectangle to demonstrate the placement of the x and y axes and the calculation of the hydrostatic force.
- 📊 For a triangular object, the script shows how to find the equation of the triangle's side in terms of y to calculate the length of the stripe and the hydrostatic force.
- 🏗️ The script addresses a trapezoidal dam and explains how to calculate the hydrostatic force using the trapezoid's dimensions and the water's depth.
- ⭕ The calculation for a circular object involves using the circle's radius and the depth of submersion to find the hydrostatic force.
- 📘 The script introduces the concept of symmetric functions in integrals, which simplifies the calculation by allowing the integral from -a to a to be computed as twice the integral from 0 to a for even functions.
- 📝 The final answers for the hydrostatic force are given in units consistent with the units used in the problem statement: pounds for feet and Newtons for meters.
Q & A
What are the dimensions of the rectangle submerged underwater in the first example?
-The rectangle has a width of 2 feet and a height of 8 feet. It is submerged 3 feet underwater.
How is the x-axis and y-axis positioned on the submerged rectangle?
-The x-axis is placed at the base of the rectangle with the positive direction to the right. The y-axis is placed in the middle of the object with the positive direction upwards.
What is the formula to calculate the hydrostatic force on the submerged object?
-The formula is the integral from A to B of the density times the length times the depth, with respect to y (dy).
What values are used for density and force units when the length is in feet?
-The density is 62.5 and the force is measured in pounds.
What is the depth in the hydrostatic force formula, and how is it calculated for the rectangle?
-The depth is the distance from the stripe to the surface of the water. It is calculated as 11 minus y, where 11 is the sum of the height of the rectangle (8 feet) and the depth it is submerged (3 feet).
How is the hydrostatic force calculated for a triangular object submerged in water?
-The hydrostatic force is calculated by integrating the force exerted by each stripe of water over the height of the triangle, with the density and length parameters adjusted accordingly.
What is the equation used to convert the length of the stripe into a function of y for the triangle?
-The equation used is y = -1/2x + 5, which is derived from the coordinates and slope of the triangle.
How is the length of the stripe determined for the trapezoidal dam example?
-The length of the stripe is determined as 2 times x, where x is derived from the equation y = 2x - 30, converted into y + 30 = 2x.
What is the depth of the stripe for the trapezoidal dam example?
-The depth is calculated as 16 minus y, where 16 is the distance from the surface of the water to the x-axis at the bottom of the trapezoid.
How is the hydrostatic force on a cylindrical drum calculated?
-The hydrostatic force is calculated by integrating the force exerted by each stripe of water over the height of the circle, with the density, length, and depth parameters adjusted accordingly.
Outlines
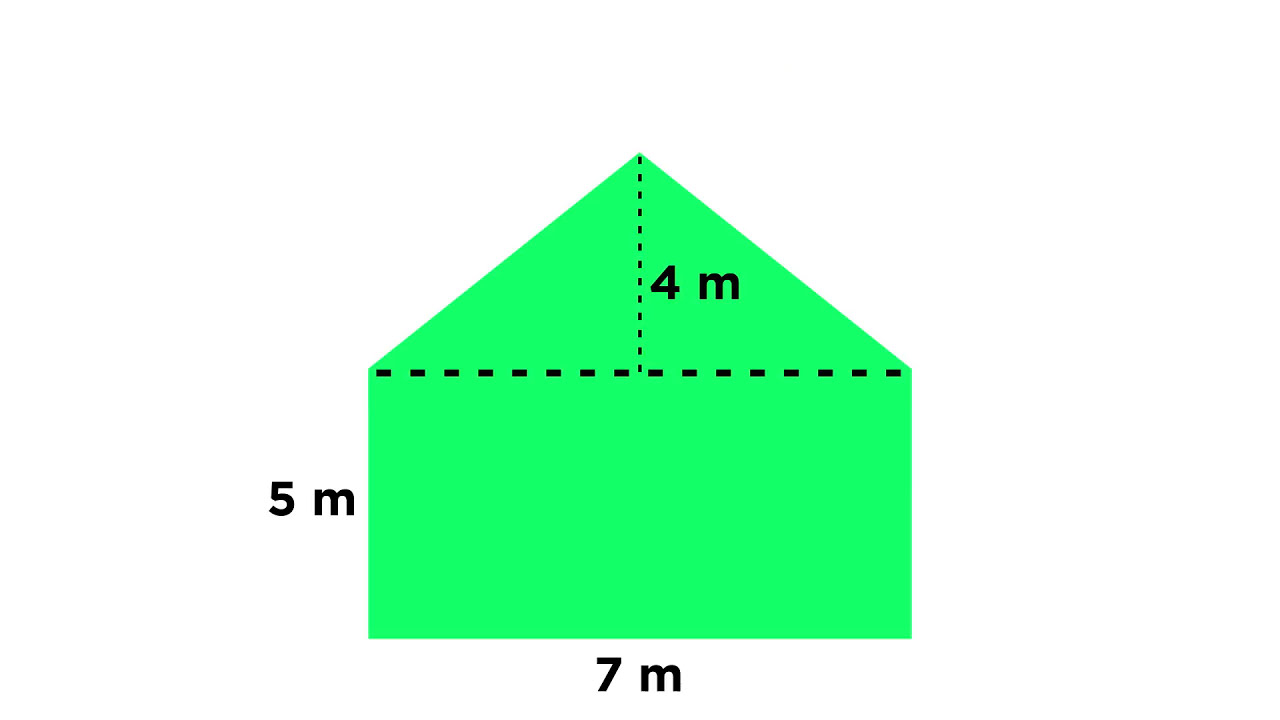
📚 Hydrostatic Force Calculation on a Submerged Rectangle
This paragraph explains how to calculate the hydrostatic force on a rectangular object submerged in water. The object has dimensions of width two feet, height eight feet, and is submerged to a depth of three feet. The process involves setting up the X and Y axes on the rectangle, understanding the concept of calculating the force on stripes of water acting on the object, and summing these forces to find the total hydrostatic force. The formula for hydrostatic force is given by the integral from A to B of the product of density, length, and depth (dy). The example uses a density of 62.5 pounds per cubic foot, appropriate for measurements in feet, and demonstrates the calculation process, resulting in a force of 7000 pounds.
📐 Hydrostatic Force on a Submerged Triangular Object
The second paragraph delves into calculating the hydrostatic force on a triangular object submerged in water. The triangular object has a base width of 10 feet, a height of 5 feet, and is submerged to a depth of 2 feet. The explanation includes setting the X and Y axes on the triangle, calculating the force on individual stripes of the triangle, and summing these to find the total hydrostatic force. The formula for hydrostatic force is applied with a density of 62.5 pounds per cubic foot. The length of the stripe is expressed in terms of Y using the triangle's slope, and the depth is calculated as the distance from the stripe to the water surface. The final answer is given as 833.33 pounds.
🏗️ Hydrostatic Pressure on a Trapezoidal Dam
This paragraph focuses on calculating the hydrostatic force on a trapezoidal dam submerged in water. The dam has a top width of 50 meters, a bottom width of 30 meters, and a height of 20 meters, with 4 meters of water above the dam's top. The process involves setting the X and Y axes on the dam, calculating the force on each stripe of the dam, and summing these to find the total hydrostatic force. The formula for hydrostatic force is applied with a density of 9800 Newtons per cubic meter. The length of the stripe is converted from X to Y, and the depth is calculated as the distance from the stripe to the water surface. The final answer is given as 4.4 x 10^7 Newtons.
⭕ Hydrostatic Force on a Submerged Circular Drum
The fourth paragraph discusses calculating the hydrostatic force on a cylindrical drum, represented as a circle with a radius of three feet, submerged to a depth of 10 feet. The explanation includes setting the X and Y axes at the center of the circle, calculating the force on each stripe of the circle, and summing these to find the total hydrostatic force. The formula for hydrostatic force is applied with a density of 62.5 pounds per cubic foot. The length of the stripe is expressed in terms of Y using the circle's radius, and the depth is calculated as the distance from the stripe to the water surface. The integral is simplified using the properties of even and odd functions, and the final answer is given as 12,370 pounds.
🔢 Practice Problem: Hydrostatic Force on a Submerged Circle
The final paragraph presents a practice problem involving the calculation of hydrostatic force on a circle submerged in water. The circle has a radius of 8 meters and is submerged to a depth of 4 meters. The explanation suggests using the same method as demonstrated in the previous paragraphs and provides an approximate answer of 2.36 x 10^7 Newtons for the hydrostatic force, assuming the problem is in meters and thus the force is in Newtons. The paragraph concludes with an invitation for viewers to enjoy the video, ask questions, and subscribe for more content.
Mindmap
Keywords
💡Hydrostatic Force
💡Submerged
💡Rectangle
💡Integral
💡Density
💡Depth
💡Trapezoid
💡Cylinder
💡Trigonometry
💡Symmetric Functions
Highlights
Introduction to calculating hydrostatic force on submerged objects.
Example of a submerged rectangle with specific dimensions (width: 2 feet, height: 8 feet, submerged depth: 3 feet).
Explanation of setting up the coordinate system with X and Y axes.
Description of the hydrostatic force calculation method using incremental stripes of water.
Integral formula for calculating hydrostatic force: density times length times depth, integrated with respect to Y.
Units of measurement: density in feet (62.5) and force in pounds.
Example calculation for a submerged rectangle: total hydrostatic force calculated as 7000 pounds.
Introduction to hydrostatic force calculation for a submerged triangle.
Setup of coordinate system for a triangle and explanation of calculating incremental forces.
Conversion of variables to set up the integral in terms of Y.
Final calculation for the triangle: hydrostatic force of 833.33 pounds.
Introduction to hydrostatic force calculation for a submerged trapezoid.
Setting up the trapezoid dimensions and coordinate system for integration.
Deriving the length of each stripe and depth for the trapezoid.
Final calculation for the trapezoid: hydrostatic force of 4.4 x 10^7 Newtons.
Introduction to hydrostatic force calculation for a submerged circle.
Setting up the circle and deriving the integral in terms of Y for the circular object.
Final calculation for the circular object: hydrostatic force of 12,370 pounds.
Example problem for practice with a circle submerged 4 meters with a radius of 8 meters.
Encouragement to ask questions and subscribe for more educational content.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: