Sect 8 3 #6 Hydrostatic Force, Calculus 2

blackpenredpen
25 Apr 201506:32
EducationalLearning
32 Likes 10 Comments

TLDRThe video script demonstrates the calculation of hydrostatic force on a triangular plate submerged vertically in water. It explains the use of integration to account for varying pressures at different depths, employing the formula force = pressure x area. The area calculation involves deriving the equation of the triangle's base from its slope and integrating over the strip's width. The force is then calculated by integrating the product of water density, the area of the rectangle, and the depth, yielding a result in Newtons, approximately 3.3 x 10^5 N.

Takeaways
  • 📚 The calculation involves finding the hydrostatic force on a triangular plate submerged vertically in water.
  • 📐 The formula for force is pressure times area, which requires integration due to varying pressure with depth.
  • 🌊 The pressure at a point is the product of the distance below the surface, the density of water, and the acceleration due to gravity (9.8 m/s²).
  • 🔢 The density of water is approximated as 1000 kg/m³ for the calculation.
  • 📏 The area of the plate is determined by integrating over the variable y, using a rectangular strip method.
  • 📈 The equation of the line forming the triangular plate is derived from the coordinates of the base of the triangle.
  • 📉 The slope of the line (m) is calculated as 5/2, and the y-intercept (b) is 5, leading to the equation y = (5/2)x + 5.
  • 🔍 The relationship between x and y is inverted to express x in terms of y, which is crucial for the area calculation.
  • 📝 The area of the small rectangle for integration is 2x * Dy, where x is expressed as a function of y.
  • 🧩 The integral is set up by multiplying the area of the rectangle by the density of water and the distance from the surface (5 - y).
  • 📊 The final step is to integrate the expression from y = 0 to y = 5 to find the total hydrostatic force on the plate.
  • 🔑 The result of the integral gives the force in Newtons, which is approximately 3.3 * 10^5 N for this scenario.
Q & A

  • What is the main objective of the script?

    -The main objective of the script is to calculate the hydrostatic force acting on a triangular plate submerged vertically in water.

  • Why is integration used in this calculation?

    -Integration is used because the pressure acting on the plate varies depending on the depth, necessitating the summation of these pressures over the entire submerged area.

  • What is the formula for hydrostatic pressure?

    -The hydrostatic pressure at a certain depth is given by the formula: Pressure = Depth × Density of the fluid.

  • What are the units and values used for the density of water in this calculation?

    -The units used are meters for distance and the density of water is taken as 9.8 m/s² multiplied by 1000 kg/m³.

  • How is the area of the plate related to the small rectangle in the script?

    -The area of the plate is conceptualized as a series of small rectangles (strips) along the y-axis, with the area of each small rectangle being 2x * Dy, where x is a function of y.

  • What is the equation of the line representing the triangular plate?

    -The equation of the line is derived from the slope (m = 5/2) and the y-intercept (b = 5), resulting in y = (5/2)x + 5.

  • How is the x-coordinate of a point on the plate related to its y-coordinate?

    -The x-coordinate is found by rearranging the line equation to x = -(2/5)y + 2.

  • What is the expression for the area of the small rectangle in terms of y?

    -The area of the small rectangle is given by 2 * (-2/5)y + 2 multiplied by Dy, where Dy is a small change in the vertical distance.

  • What is the integral set up to calculate the force acting on the plate?

    -The integral is set up as the product of the area of the small rectangle, the density of water, and the depth (5 - y), integrated from y = 0 to y = 5.

  • What is the final result of the integral representing the force on the triangular plate?

    -The final result of the integral, after calculation, is approximately 3.3 * 10^5 Newtons.

  • What does the result of the integral represent in the context of the problem?

    -The result represents the total hydrostatic force acting on the triangular plate when it is submerged vertically in water.

Outlines
00:00
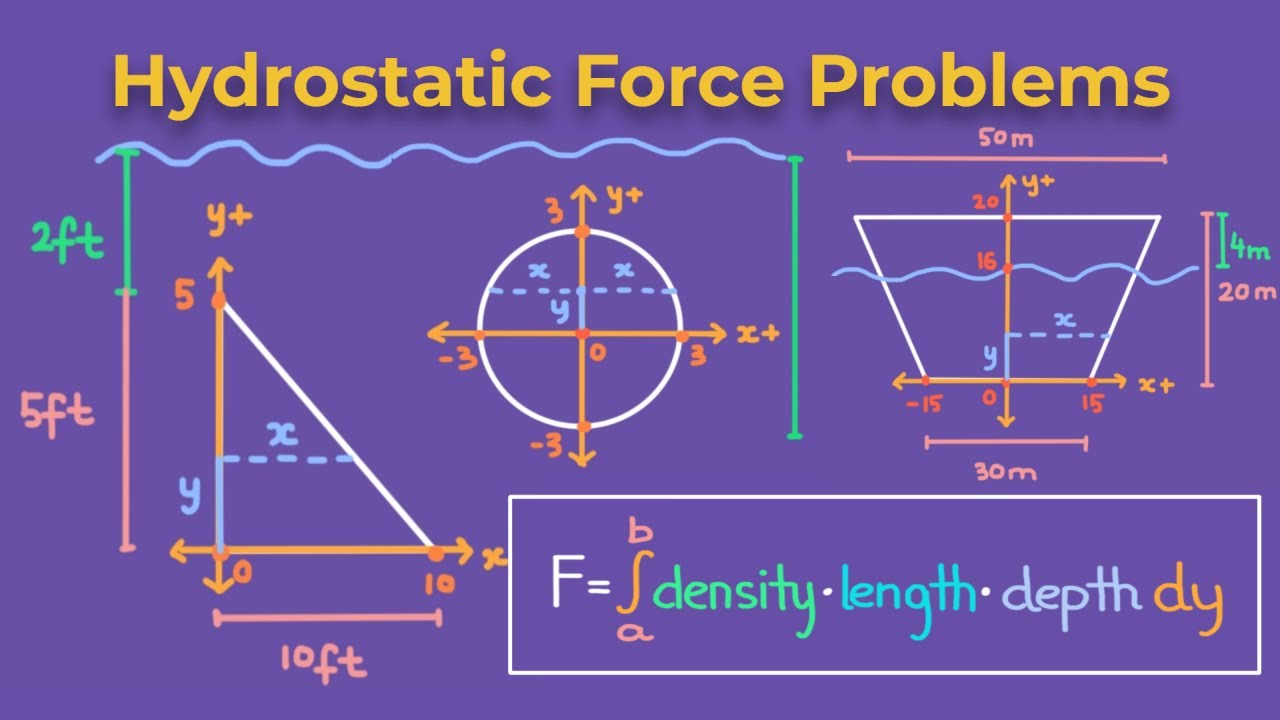
📚 Calculating Hydrodynamic Force on a Triangular Plate

This paragraph introduces the concept of calculating the hydrodynamic force acting on a triangular plate submerged vertically in water. The force is determined by integrating the pressure over the area of the plate, with pressure varying with depth due to water density. The density of water is given as 9.8 m/s² multiplied by 1000 kg/m³. The area calculation involves a rectangular strip and requires establishing a relationship between x and y coordinates based on the slope of the triangular plate's base. The equation of the line is derived from the slope and y-intercept, allowing for the expression of x in terms of y, which is crucial for the area calculation of the rectangle. The integral set up involves the area formula for the rectangle, the density of water, and the pressure formula, which includes the depth (distance from the water surface).

05:01
🔍 Integrating to Determine Force on a Submerged Triangle

The second paragraph continues the discussion on calculating the hydrodynamic force, focusing on the integration process. It explains how to determine the distance of the rectangular strip from the water surface, which is essential for calculating the pressure at different depths. The distance is calculated as the total depth minus the current depth (y), with the total depth being 5 meters. The force acting on the rectangle is then found by multiplying the area by the pressure, which includes the water density and the distance from the surface. The final step is to integrate this force over the entire depth of the plate, from y=0 to y=5, to find the total hydrodynamic force. The result of this integration is approximately 3.3 x 10^5 Newtons, as per the given script.

Mindmap
Keywords
💡Hydrostatic force
Hydrostatic force refers to the pressure exerted by a fluid at rest on an object submerged in it. In the video, the concept is central to calculating the force acting on a triangular plate when it is placed vertically in water. The script discusses how this force is determined by integrating the pressure over the area of the plate, which varies with depth due to the fluid's density and gravity.
💡Pressure
Pressure in this context is the force per unit area exerted by the water on the submerged plate. The script explains that pressure is a function of depth, with deeper parts of the plate experiencing greater pressure due to the weight of the overlying water column.
💡Integration
Integration is a mathematical process used to calculate the accumulated effect of varying quantities over a range. In the script, integration is necessary to find the total hydrostatic force on the triangular plate because the pressure—and thus the force—changes with depth.
💡Density
Density is defined as mass per unit volume and is a key factor in calculating hydrostatic pressure. The script specifies the density of water as 1,000 kg/m³, which is used in conjunction with the gravitational acceleration to determine the pressure at different depths.
💡Area
The area of the submerged plate is crucial for calculating the force exerted by the water. The script describes a method to determine the area of an infinitesimal strip of the plate, which is then integrated to find the total area subjected to the water's pressure.
💡Reference frame
A reference frame is a set of coordinates used to describe the position and motion of objects. The script uses a reference frame to establish a coordinate system for the triangular plate, which aids in the calculation of the area and the force acting on it.
💡Slope
Slope is a measure of the steepness of a line, defined as the ratio of the vertical change to the horizontal change. In the script, the slope of the triangular plate's hypotenuse is calculated to establish the relationship between x and y coordinates, which is essential for determining the area of the plate.
💡Equation of a line
The equation of a line is used to describe the relationship between the x and y coordinates of points on a line. The script derives the equation of the line forming the triangular plate's hypotenuse to express x in terms of y, which is necessary for the area calculation.
💡Infinitesimal strip
An infinitesimal strip is a very thin slice of an object, used in calculus to approximate the area under a curve. The script describes using a rectangle with an infinitesimal height (Dy) to represent a small portion of the triangular plate's area for integration purposes.
💡Gravitational acceleration
Gravitational acceleration is the acceleration due to gravity, approximately 9.8 m/s² on Earth. The script uses this value to calculate the pressure at different depths in the water, which is then used to find the hydrostatic force on the plate.
💡Force calculation
Force calculation in the script involves integrating the product of pressure, area, and distance to find the total hydrostatic force on the triangular plate. The process involves using the derived equations for area and pressure to perform the integration over the entire depth of the plate.
Highlights

Force is calculated as pressure times area, necessitating integration due to varying pressure with depth.

Pressure formula used is distance times density, with water density taken as 9.8 m/s² multiplied by 1000 kg/m³.

Area calculation involves a rectangle strip with dimensions 2x * Dy.

Reference frame is established with x and y axes at the midpoint of the base of the triangle.

The equation of the line forming the triangle's base is derived from its slope and y-intercept.

Slope of the line is calculated as 5/2, indicating a steep incline.

Y-intercept is determined to be 5, establishing the starting point of the line equation.

The equation Y = (-5/2)x + 5 is derived for calculating x in terms of Y.

Integration of the area of the rectangle strip is set up using the derived equation for x.

The integral includes the area calculation for the entire submerged part of the triangle.

Density of water is factored into the integral to account for varying pressure with depth.

Distance from the water surface to the rectangle strip is calculated as 5 - y.

The force acting on the rectangle is expressed as an integral from y=0 to y=5.

The final integral calculation for the force on the triangular plate is performed.

The result of the integral provides an approximate force of 3.3 * 10^5 Newtons.

The force is measured in Newtons, indicating the magnitude of the hydrostatic force on the plate.

Transcripts

Browse More Related Video

What is Pressure? | Middle school physics | Khan Academy

Hydrostatic Force Problems - Calculus 2

A tank is full of water. find the work required to pump

Lecture 11: Abstracting the Integral Pyramids and Dams

AP Calculus BC exams: 2008 1 d | AP Calculus BC | Khan Academy

Hydrostatic Force Problems - Calculus 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Hydrodynamic ForceTriangular PlateIntegrationPhysicsFluid MechanicsPressure CalculationWater DensityArea CalculationForce IntegrationEngineering Analysis