Finding Local Maximum and Minimum Values of a Function - Relative Extrema

The Organic Chemistry Tutor
3 Mar 201814:17
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide on identifying local maximum and minimum values of a function. It explains the concept of extreme values and horizontal tangent lines at these points, emphasizing the importance of the derivative being zero. The process involves finding the first derivative, setting it to zero to solve for critical numbers, and using a sign chart to determine if these points correspond to local maxima or minima. The script provides detailed examples, demonstrating how to calculate derivatives, factor them, and apply the sign chart method to ascertain relative extrema. The examples cover various functions and their corresponding critical points, effectively illustrating the mathematical techniques involved.

Takeaways
  • 📈 To find local maximum and minimum values of a function, look for points where the derivative is zero (horizontal tangent line).
  • 🔍 The first step is to find the first derivative of the function and set it equal to zero to solve for critical numbers.
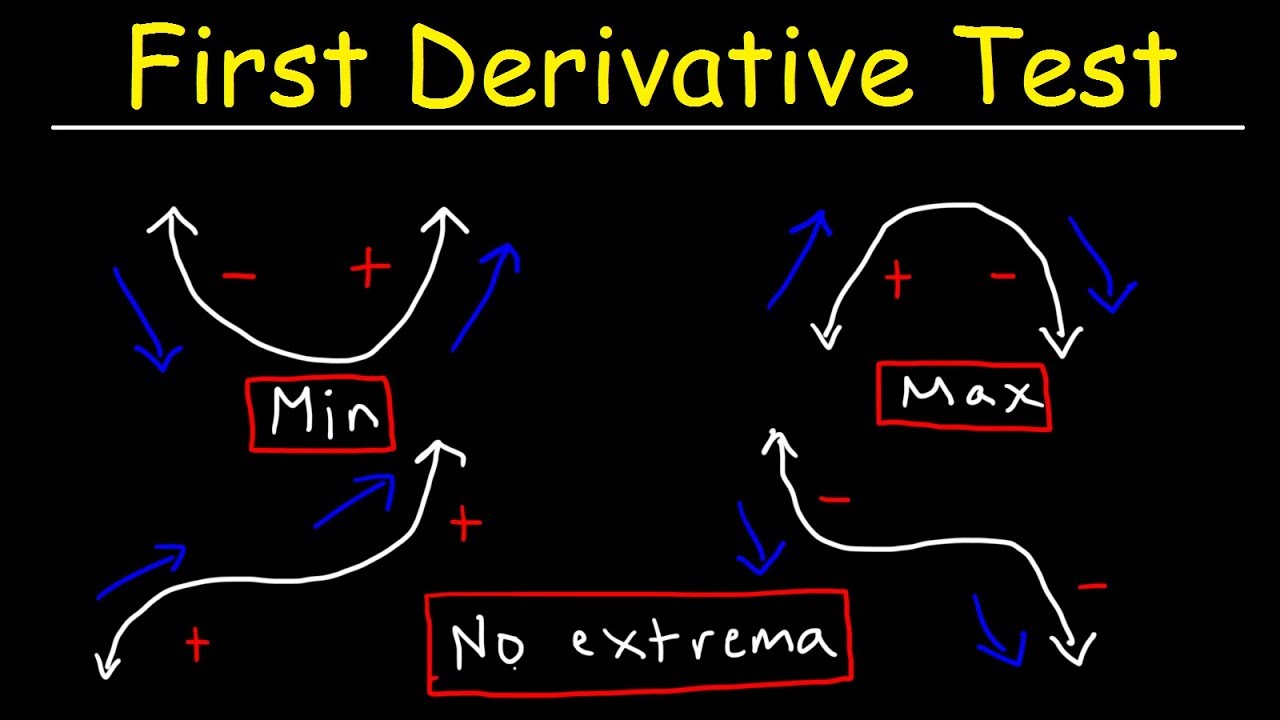
  • 📊 A sign chart can be used to determine if a critical number corresponds to a local maximum, local minimum, or neither.
  • 🌐 For a local minimum, the derivative changes from negative to positive, indicating the function is decreasing before and increasing after.
  • 🔄 At a local maximum, the derivative changes from positive to negative, indicating the function is increasing before and decreasing after.
  • 📐 The shape of the function around critical numbers can be analyzed by plugging in values into the first derivative.
  • 🔢 To find the exact local maximum or minimum value, evaluate the original function at the critical number(s).
  • 💻 In examples, the process of finding critical numbers and analyzing the function's behavior was demonstrated with specific functions.
  • 🧩 Factoring the first derivative can help in identifying the critical numbers and understanding the function's behavior.
  • 🔄 The multiplicity of factors in the first derivative (odd or even) affects the sign change across critical numbers.
  • 📍 The process can be applied to various functions to identify local extrema without necessarily finding the exact y-coordinates unless required.
Q & A

  • What is the main focus of the video?

    -The main focus of the video is to teach viewers how to identify the local maximum and minimum values of a function.

  • What is a horizontal tangent line at extreme values?

    -At extreme values, a horizontal tangent line means that the derivative of the function at that point is equal to zero.

  • How do you find the location of local maximum and minimum values?

    -To find the location of local maximum and minimum values, you need to find the first derivative of the function, set it equal to zero, and solve for x. These solutions are the critical numbers.

  • What is the significance of a sign chart in identifying local extrema?

    -A sign chart is used to determine whether a critical number corresponds to a local maximum, local minimum, or neither by analyzing the sign of the first derivative on either side of the critical number.

  • What is the first derivative of the function f(x) = x^2 - 4x?

    -The first derivative of the function f(x) = x^2 - 4x is f'(x) = 2x - 4.

  • How does the shape of the function change around a local minimum?

    -Around a local minimum, the function is decreasing when the first derivative is negative and increasing when the first derivative is positive. The function changes from negative to positive at the local minimum point.

  • What are the critical numbers for the function f(x) = 2x^3 + 3x^2 - 12x?

    -The critical numbers for the function f(x) = 2x^3 + 3x^2 - 12x are x = -2 and x = 1.

  • How does the multiplicity of a factor in the first derivative affect the sign of the function?

    -If the multiplicity is an odd number, the sign will change across the critical number. If it's even, the sign will remain the same.

  • What is the first derivative of the function f(x) = 3x^4 - 16x^3 + 24x^2?

    -The first derivative of the function f(x) = 3x^4 - 16x^3 + 24x^2 is f'(x) = 12x^3 - 48x^2 + 48x.

  • What are the critical numbers for the function f(x) = 3x^4 - 16x^3 + 24x^2?

    -The critical numbers for the function f(x) = 3x^4 - 16x^3 + 24x^2 are x = 0 and x = 2.

  • How can you determine if a critical number is a local maximum or minimum without finding the y-coordinate?

    -You can determine if a critical number is a local maximum or minimum by observing the sign of the first derivative and how it changes around the critical number. If the sign changes from positive to negative, it indicates a local maximum, and if it changes from negative to positive, it indicates a local minimum.

Outlines
00:00
📈 Identifying Local Maximum and Minimum Values

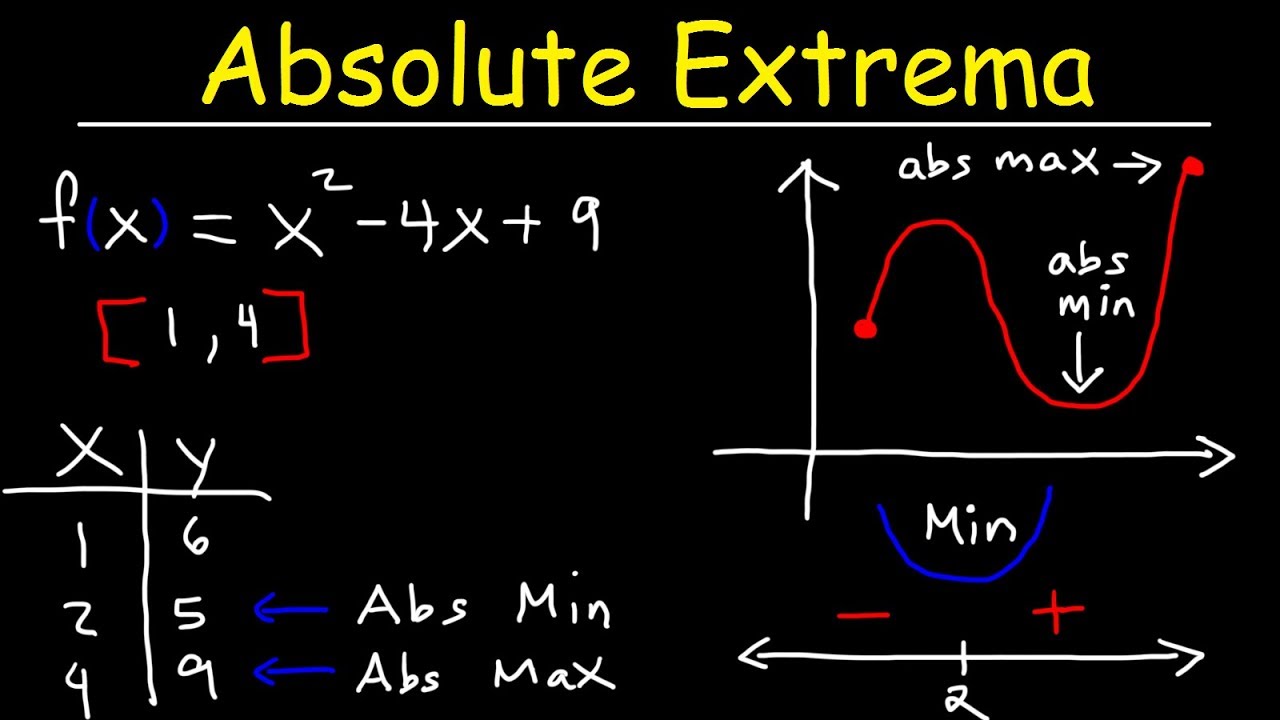
This paragraph introduces the concept of identifying local maximum and minimum values of a function. It explains that at these extreme points, the function has a horizontal tangent line, meaning the derivative is zero. The process involves finding the first derivative of the function, setting it to zero, and solving for x to get the critical numbers. A sign chart can then be used to determine if a critical number corresponds to a local maximum or minimum. The example function f(x) = x^2 - 4x is used to illustrate these steps, leading to the identification of a local minimum at x=2 with a value of -4.

05:01
🔢 Solving for Relative Extrema with Polynomial Functions

The second paragraph continues the discussion on finding local maximum and minimum values, focusing on a different function, f(x) = 2x^3 + 3x^2 - 12x. The first derivative is calculated, and critical numbers are determined by setting the derivative equal to zero. A sign chart is constructed to analyze the behavior of the function around the critical numbers. The function is found to have a relative maximum at x=-2 and a relative minimum at x=1, with the corresponding y-coordinates being 20 and -7, respectively.

10:03
📊 Locating Relative Extreme Points in Quartic Functions

The final paragraph addresses the process of identifying relative extreme points in a quartic function, f(x) = 3x^4 - 16x^3 + 24x^2. The first derivative is calculated, and the greatest common factor is factored out to simplify the equation. Critical numbers are found by setting each factor of the derivative equal to zero. A sign chart is used to analyze the function's behavior, leading to the conclusion that there is a minimum at x=0, while x=2 does not represent a maximum or minimum due to the nature of the function's increase at that point.

Mindmap
Keywords
💡Local Maximum
A local maximum is a point on a graph of a function where the function reaches a peak or highest value in a given neighborhood. In the context of the video, it is one of the extreme values of the function that we are interested in identifying. The video explains that at a local maximum, the derivative (or slope of the function) is zero, and the function changes from increasing to decreasing. An example from the script is the function f(x) = x^2 - 4x, where setting the first derivative to zero helps us find the critical number x=2, which corresponds to a local minimum, not a maximum.
💡Local Minimum
A local minimum is a point on the graph of a function where the function reaches a trough or lowest value in a given neighborhood. The video emphasizes the importance of identifying these points to understand the behavior of the function. At a local minimum, similar to a local maximum, the derivative is zero, but the function changes from decreasing to increasing. The video provides an example of a local minimum at x=2 for the function f(x) = x^2 - 4x, where the first derivative 2x - 4 changes from negative to positive, indicating a local minimum.
💡Derivative
The derivative of a function is a fundamental concept in calculus that represents the rate of change or the slope of the function at a given point. In the video, the process of finding the derivative of a function is crucial for identifying local maximum and minimum points. By setting the first derivative equal to zero, we can find the critical numbers where potential extrema occur. For instance, the derivative of f(x) = x^2 - 4x is 2x - 4, and setting this equal to zero helps us find the critical number x=2.
💡Critical Numbers
Critical numbers are the values of the independent variable (usually x) at which the derivative of a function is either zero or undefined. These points are significant because they represent potential local maximum or minimum values of the function. The video script involves finding critical numbers by setting the first derivative of given functions to zero and solving for x. For example, for the function f(x) = x^2 - 4x, the critical number is found by setting the first derivative 2x - 4 equal to zero, which gives x=2.
💡Horizontal Tangent Line
A horizontal tangent line is a tangent line to a graph of a function that is parallel to the x-axis, meaning it has a slope of zero. In the context of the video, it is mentioned that at extreme values such as local maximums and minimums, the function will have a horizontal tangent line. This is indicative of the function's derivative being zero at these points, as zero slope corresponds to a horizontal line.
💡Sign Chart
A sign chart is a tool used in calculus to determine the behavior of a function around its critical numbers. By testing the sign of the first derivative on intervals created by the critical numbers, we can determine whether the function is increasing or decreasing in those intervals. This helps in identifying whether the critical numbers correspond to local maxima, local minima, or neither. The video script describes the use of a sign chart to determine the nature of critical numbers by plugging in values into the first derivative and observing the sign changes.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of other polynomials or factors. This is an essential step in simplifying expressions and solving equations. In the video, factoring is used to simplify the first derivative of a function before setting it equal to zero to find critical numbers. For example, the derivative of f(x) = 2x^3 + 3x^2 - 12x is factored into (x + 2)(x - 1) to find the critical numbers x=-2 and x=1.
💡Greatest Common Factor (GCF)
The greatest common factor (GCF) is the largest factor that a set of numbers or terms has in common. In the context of the video, the GCF is used to simplify expressions by factoring out the common terms from a polynomial. This simplification process helps in setting the derivative equal to zero and solving for critical numbers more efficiently. For instance, in the derivative of f(x) = 3x^4 - 16x^3 + 24x^2, the GCF of 12x is factored out, leading to the simplified expression 12x(x^3 - 4x + 2).
💡Multiplicity
Multiplicity refers to the number of times a factor appears in a factored expression. It is particularly important when analyzing the behavior of a function around critical numbers. In the video, the concept of multiplicity is used to determine the change in sign of the first derivative as we move from one interval to another. If the multiplicity is odd, the sign changes; if it's even, the sign remains the same. This helps in identifying local maxima and minima.
💡Ordered Pairs
Ordered pairs are pairs of numbers that represent the coordinates of a point in a two-dimensional space, typically with the first number being the x-coordinate and the second number being the y-coordinate. In the context of the video, ordered pairs are used to specify the location and value of local maxima and minima. The video shows how to find the x-coordinates of critical points and then use the original function to find the corresponding y-coordinates, forming the ordered pairs that describe the extrema.
💡Relative Extrema
Relative extrema, also known as local extrema, are the highest or lowest points of a function within a specific interval or on the entire domain of the function. The video focuses on identifying these points by finding the critical numbers where the derivative is zero and then using a sign chart to determine if these points correspond to a local maximum or minimum. The process helps in understanding the behavior of the function and its variations within different intervals.
Highlights

The video focuses on identifying local maximum and minimum values of a function, which are essential for understanding the behavior of the function.

At local maximum and minimum points, the function has a horizontal tangent line, meaning the derivative at these points equals zero.

To find local extrema, one must first find the first derivative of the function and set it equal to zero to solve for critical numbers.

The sign chart is a useful tool for determining whether a critical number corresponds to a local maximum, local minimum, or neither.

For the function f(x) = x^2 - 4x, the first derivative is 2x - 4, and setting it to zero yields a critical number of x = 2.

At x = 2, the function f(x) = x^2 - 4x has a local minimum value, with the y-coordinate being -4.

In the example of f(x) = 2x^3 + 3x^2 - 12x, the first derivative is 6x^2 + 6x - 12, and setting it to zero gives critical numbers of x = -2 and x = 1.

For the function with the critical numbers x = -2 and x = 1, the local maximum occurs at x = -2, and the local minimum at x = 1.

When the multiplicity of a factor in the first derivative is odd, the sign changes from positive to negative or vice versa across that critical number.

The example of f(x) = 3x^4 - 16x^3 + 24x^2 demonstrates the process of finding critical numbers without needing to find the y-coordinates.

The first derivative of the function f(x) = 3x^4 - 16x^3 + 24x^2 is 12x^3 - 4x^2 + 48x, and setting it to zero gives critical numbers of x = 0 and x = 2.

At x = 0, the function has a local minimum, and at x = 2, it neither increases nor decreases, indicating no local maximum or minimum.

The process of identifying local extrema is crucial for various applications in mathematics, physics, and engineering.

Understanding the behavior of functions at local extrema can help in optimizing functions and solving real-world problems.

The video provides a clear and detailed explanation of the process of finding local maximum and minimum values, making it accessible for learners.

The use of sign charts and factoring techniques in the video helps to visualize and understand the changes in the function's slope.

The video's step-by-step approach to finding critical numbers and analyzing the function's behavior is an effective teaching method.

The video demonstrates the importance of understanding the mathematical concepts behind finding local extrema and their practical applications.

Transcripts

Browse More Related Video

Finding Absolute Maximum and Minimum Values - Absolute Extrema

First Derivative Test

Finding Relative Extrema

3.1 - Using First Derivatives to Classify Max and Min Values

Second Derivative Test Multivariable (Calculus 3)

Finding Critical Numbers

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusDerivativesLocal ExtremaCritical NumbersMath EducationFunction AnalysisGraphing TechniquesMax/Min ProblemsMath TutorialEducational Content