Lesson 12 - Calculating Volume With Integrals (Calculus 1 Tutor)

Math and Science
4 Mar 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script introduces the concept of using integrals to calculate volumes, a method derived from calculus. It explains how rotating a function around an axis, such as the x-axis, can create a volume. The example given involves rotating a function to form a symmetrical shape, and then calculating the volume by considering the area of cross-sections. The script emphasizes the difficulty of calculating such volumes without calculus and provides an intuitive understanding of how integrals can be applied to find the volume of complex shapes.

Takeaways
  • πŸ“ˆ Integrals can be used to calculate volumes, extending beyond their traditional role in representing areas.
  • πŸ“š The formulas known from geometry, such as the volume of a sphere (4/3 PI R cubed), can be derived using calculus.
  • πŸŒ€ Rotating a curve around an axis can generate a volume, which may be complex to calculate without calculus.
  • πŸ“Š By rotating a function f(X) around the x-axis, a symmetrical shape is formed, which can be used to understand volume calculation.
  • 🎨 Visualization of the three-dimensional shape resulting from the rotation helps in conceptualizing the volume.
  • πŸ”„ The cross-section of the rotated shape is a circle, with the radius being the function value f(X) at each point along the x-axis.
  • 🌐 The area of the cross-sectional slice is given by PI * (f(X)^2), representing the circle created by the rotation.
  • 🧩 Integrals sum up infinitesimally thin slices of a graph to calculate larger quantities, such as volume.
  • πŸ“ˆ The concept of integrals allows for the calculation of volumes of shapes that are difficult to measure using traditional methods.
  • πŸ’‘ Calculating the volume of a shape with a complex curve can be achieved through calculus, which would otherwise be challenging.
  • πŸ“– Understanding the relationship between the function, its rotation, and the resulting volume is crucial for applying calculus in volume calculations.
Q & A

  • How can integrals be used in calculus beyond calculating area?

    -Integrals can be generalized to calculate volume, not just area. This expands their application from 2-dimensional to 3-dimensional calculations.

  • Can the volume of complex shapes be derived from calculus?

    -Yes, formulas for the volume of complex shapes, like the volume of a sphere, can be derived using calculus, demonstrating its foundational role in geometric calculations.

  • What is an example of using calculus to calculate volume?

    -An example is rotating a curve around an axis to form a 3-dimensional shape, such as a vase, and then calculating its volume through integration.

  • How does rotating a curve around the x-axis help in calculating volume?

    -Rotating a curve around the x-axis forms a symmetrical 3D shape whose volume can be calculated by integrating the area of infinitesimally thin slices of the shape.

  • Why is it difficult to calculate the volume of a vessel with a curved shape using traditional methods?

    -Traditional methods struggle with curved shapes because these shapes can have complex, non-uniform geometries that are hard to measure or calculate without calculus.

  • What does the function \(f(x)\) represent in the context of rotating a curve to calculate volume?

    -The function \(f(x)\) represents the distance from the x-axis to the curve at any given point, which becomes the radius of a circular cross-section when the curve is rotated around the x-axis.

  • How is the area of a slice of the rotated shape calculated?

    -The area of a slice is calculated using the formula for the area of a circle, \(Ο€r^2\), where \(r\) is the radius, represented by \(f(x)\) in this context, leading to the formula \(Ο€[f(x)]^2\).

  • What role do integrals play in calculating the volume of a rotated shape?

    -Integrals add up the area of infinitely many, infinitesimally thin slices (circular cross-sections) of the rotated shape to calculate its overall volume.

  • Why is the concept of slices important in integrating to find volume?

    -The concept of slices is crucial because it allows the division of a complex 3D shape into manageable 2D shapes (circles), whose areas can be easily calculated and then integrated over.

  • What is the significance of the formula \(Ο€[f(x)]^2\) in the context of volumes of rotation?

    -The formula \(Ο€[f(x)]^2\) is significant because it represents the area of a circular cross-section of a rotated shape, serving as the basis for integrating over a range to find the shape's volume.

Outlines
00:00
πŸ“š Introduction to Calculating Volume with Integrals

This paragraph introduces the concept of using integrals for calculating volumes, which is a departure from their traditional use of representing areas. It explains that while integrals are well-known for their role in geometry and area calculations, they can also be utilized to determine the volume of shapes. The speaker sets the stage for a deeper exploration into this topic by mentioning that formulas familiar from geometry, such as the volume of a sphere (4/3 PI R cubed), can all be derived from calculus. The paragraph emphasizes the power of calculus and integrals in generalizing volume calculations, and teases the upcoming demonstration of this principle through quick problems.

Mindmap
Keywords
πŸ’‘Integrals
Integrals are fundamental components of calculus, representing the accumulation of quantities, such as areas under curves. In the context of the video, integrals are described as tools not only for determining areas but also for calculating volumes. This expansion of the integral's application illustrates its versatility in solving more complex geometric problems, such as finding the volume of three-dimensional shapes generated by rotating a curve around an axis.
πŸ’‘Volume
Volume refers to the amount of space occupied by a three-dimensional object. The video explains how calculus, particularly through the use of integrals, can be employed to calculate the volume of objects with complex shapes. This concept is highlighted with the example of deriving the volume formula for a sphere using calculus, showcasing the method's ability to generalize volume calculation beyond simple geometric shapes.
πŸ’‘Geometry
Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, and solids. In the video, geometry serves as a foundation for understanding the volume of simple shapes, which calculus then extends to more complex forms through integrals. This connection emphasizes the relationship between calculus and geometry, demonstrating how calculus builds upon and extends geometric principles.
πŸ’‘Function
A function in mathematics is a relation that uniquely associates members of one set with members of another set. The video discusses how functions, denoted as f(x), represent mathematical relationships that can be graphed on a coordinate plane. These functions become central in calculus for modeling curves that, when rotated around an axis (like the x-axis), create volumes that can be calculated through integration.
πŸ’‘Axis Rotation
Axis rotation refers to the process of rotating a two-dimensional shape around an axis to generate a three-dimensional object. The video uses this concept to explain how volumes of objects, created by rotating a curve defined by a function f(x) around the x-axis, can be determined. This method illustrates a geometric approach to understanding volumes in calculus, showing how rotating a curve can form complex shapes whose volumes are calculable.
πŸ’‘Radius
The radius is a straight line from the center of a circle to its circumference or from the center of a sphere to its surface. In the video, the radius concept is applied to calculus by considering the distance from the x-axis to the curve as the radius (r), which varies along the curve. This varying radius is crucial for calculating the area of circular cross-sections formed by rotating the curve around the x-axis, further used to find the volume of the three-dimensional shape.
πŸ’‘Cross-Section
A cross-section refers to the intersection of a solid and a plane, revealing the internal structure of the solid. The video illustrates how rotating a curve around an axis creates a solid whose volume is determined by examining its circular cross-sections. These cross-sections, defined by the radius at different points along the curve, play a key role in calculating the volume through integration, demonstrating the concept's application in understanding complex geometric shapes.
πŸ’‘Circle Area Formula
The circle area formula, Ο€rΒ², calculates the area of a circle based on its radius (r). This formula is used in the video to determine the area of circular cross-sections resulting from rotating a curve around the x-axis. By integrating these areas along the length of the curve, the video explains how the volume of the resulting three-dimensional shape can be calculated, showing the integral's role in bridging simple geometric formulas with complex volume calculations.
πŸ’‘Calculus
Calculus is a branch of mathematics focused on change and motion, encompassing derivatives and integrals as its main operations. The video emphasizes calculus's role in extending basic geometric and algebraic concepts to solve more complex problems, such as calculating volumes of irregularly shaped objects. Through the example of using integrals to find volumes, calculus is presented as a powerful tool for generalizing and solving problems across various dimensions.
πŸ’‘Experimentation vs. Calculation
The video contrasts experimental methods, like filling a shape with water to measure its volume, with calculative methods offered by calculus. This distinction highlights the advantage of using calculus for determining volumes without physical experimentation, especially for complex shapes. By calculating volumes through integrals, calculus provides a precise, theoretical approach to understanding the geometry of objects, showcasing the method's efficiency and broad applicability.
Highlights

The use of integrals to calculate volume is discussed in this section.

Integrals traditionally represent area, but can also be used to calculate volume.

Familiar formulas from geometry, such as the volume of a sphere (4/3 PI R cubed), can be derived from calculus.

The principle of using integrals to calculate volume involves rotating a function around an axis to create a 3D shape.

The cross-section of the rotated function forms a circle, with the function defining the radius of the circle at each point along the x-axis.

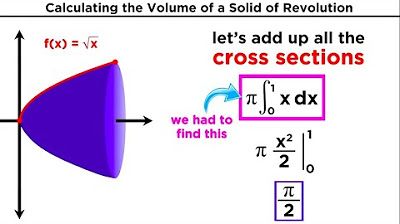
The area of the cross-section slice is calculated as PI times the function squared (PI * (f of X)^2).

Integrals sum up the areas of thin slices of a graph to calculate volume.

Calculating the volume of a shape created by rotating a curve around an axis can be challenging using traditional math but is feasible with calculus.

The curve's complexity makes it difficult to calculate volume without calculus.

The distance between points on the curve is defined by the function's value at each x-value.

The integral calculates the volume by summing the areas of all the infinitesimally thin slices.

This method of calculating volume generalizes from the cross-sectional area to the entire 3D shape.

The area of a circle formula (PI * R^2) is applied to the cross-section of the rotated function.

The integral of the function squared over a certain interval will give the volume of the shape created by rotation.

This approach to finding volume is an application of calculus that was not possible with previous mathematical methods.

The lecture aims to show the principle of calculating volume using integrals through quick problems.

The process of rotating a 2D curve around an axis to find the volume of the resulting 3D shape is a fundamental concept in calculus.

Transcripts

Browse More Related Video

Solid of Revolution (part 1)

Disc method around x-axis | Applications of definite integrals | AP Calculus AB | Khan Academy

Solid of Revolution (part 5)

Calculating the Volume of a Solid of Revolution by Integration

Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method

Lecture 20: Several Variables Volumes Galore

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegralsVolumeCalculationGeometryRotationMathematicsProblemSolvingEducationalAnalyticalThinkingCurvedSurfaces