2022 Live Review 6 | AP Physics 1 | Understanding Simple Harmonic Motion
TLDRIn this educational video, the presenter delves into the concepts of simple harmonic motion, exploring oscillators like springs and pendulums. The discussion covers the essential criteria for simple harmonic motion, including restoring force, amplitude, and period, and how they relate to various physical quantities. The video also examines the factors affecting the period of pendulums and springs, such as mass, length, and gravitational field strength, and provides practical examples and problems to reinforce understanding.
Takeaways
- 📈 The main topic of the video is simple harmonic motion, which includes oscillators like springs and pendulums.
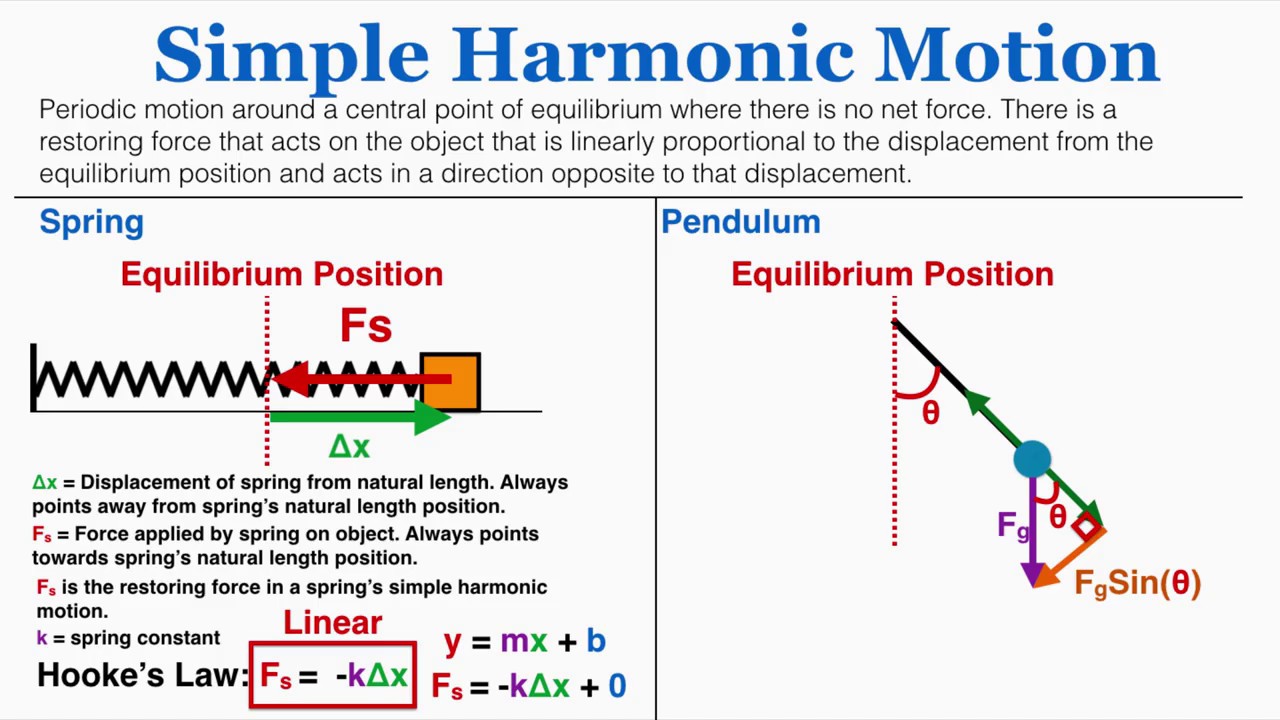
- 🔄 Simple harmonic motion requires a restoring force proportional to the displacement and in the opposite direction.
- 🏋️ For a bouncing ball, the gravitational force and displacement are not in opposite directions, so it's not simple harmonic motion.
- 🌗 The amplitude and period of simple harmonic motion are independent of each other.
- 📊 A sine or cosine graph represents the position vs. time for an object in simple harmonic motion.
- 🔧 The restoring force for a pendulum is the component of gravitational force parallel to the motion (mg * sin(theta)).
- 📈 The spring constant (k) can be found from the force-displacement graph as the slope of the graph represents the force divided by displacement.
- 🏃♂️ The maximum velocity in simple harmonic motion occurs at the equilibrium position, while the minimum velocity is at the endpoints.
- 🚀 The greatest acceleration in simple harmonic motion happens at the maximum displacement, and the smallest acceleration is at the equilibrium.
- 🌐 The period of a pendulum depends on the length of the string and the gravitational field strength, but not on the mass or amplitude.
- 🔄 The period of a spring oscillator depends on the mass of the oscillating object and the spring constant (stiffer springs have shorter periods).
Q & A
What is simple harmonic motion?
-Simple harmonic motion is a type of periodic motion where an oscillator, such as a spring or pendulum, moves back and forth under the influence of a restoring force that is directly proportional to the displacement and in the opposite direction.
What are the three requirements for an oscillator to exhibit simple harmonic motion?
-The three requirements for simple harmonic motion are: 1) There must be a restoring force that brings the object back to equilibrium, 2) The restoring force must be directly proportional to the displacement, and 3) The amplitude and period of the motion must be independent of each other.
How does the gravitational force act on a pendulum?
-The gravitational force acts on a pendulum through two components: one perpendicular to the motion (mg cos(theta)) that balances the tension force and another parallel to the motion (mg sin(theta)) that acts as the restoring force, accelerating the pendulum back towards the equilibrium position.
What is the relationship between the position and time graph of an object in simple harmonic motion?
-The position and time graph of an object in simple harmonic motion forms a sine or cosine graph, representing the oscillator's displacement from the equilibrium position over time.
How does the velocity of an object in simple harmonic motion change over time?
-The velocity of an object in simple harmonic motion is greatest at the equilibrium position, where it is moving fastest, and decreases to zero at the maximum displacement points, where it momentarily stops before changing direction.
What is the relationship between the acceleration of an object in simple harmonic motion and the restoring force?
-The acceleration of an object in simple harmonic motion corresponds to the restoring force, with the greatest acceleration occurring at the maximum displacement from equilibrium, where the restoring force is the strongest.
How does the energy of a simple harmonic oscillator change over one period?
-In one period of simple harmonic motion, the energy of the oscillator transitions between kinetic energy, when the object is passing through equilibrium, and potential energy, either spring potential energy or gravitational potential energy, when the object is at the maximum displacement points.
What factors affect the period of a pendulum?
-The period of a pendulum is affected by the length of the pendulum string and the strength of the gravitational field. It is independent of the mass of the pendulum bob and the amplitude of the swing.
What factors affect the period of a spring oscillator?
-The period of a spring oscillator is affected by the mass of the oscillating object and the spring constant (stiffness of the spring). It is independent of the amplitude of the oscillation.
How does the mass of a pendulum affect its period?
-The mass of a pendulum does not affect its period. The period of a pendulum is determined by the length of the string and the gravitational field strength, not by the mass of the pendulum bob.
How does the spring constant (k) affect the period of a spring oscillator?
-The spring constant (k) has an inverse relationship with the period of a spring oscillator. A larger spring constant results in a shorter period, as the equation for the period of a spring oscillator is T = 2π√(m/k), where m is the mass of the oscillating object.
Outlines
📚 Introduction to Simple Harmonic Motion
The video begins with Christine Gonzalez Vega introducing the topic of simple harmonic motion, which includes concepts like springs and pendulums that oscillate. The focus is on understanding the main concepts, relevant equations, and graphs associated with this type of motion. The video aims to review how these concepts can be applied in various situations, including multiple choice and free response questions. The difference between periodic motion and simple harmonic motion is highlighted, emphasizing the need for a restoring force proportional to displacement and the independence of amplitude and period in simple harmonic motion.
🔍 Analysis of Restoring Forces and Energy
The paragraph delves into the restoring forces in pendulums and springs, explaining how these forces are responsible for the oscillatory motion. The role of gravitational force in pendulums and Hooke's law for springs are discussed. The video uses diagrams to illustrate the forces acting on a pendulum and a spring. It also explores how the displacement from equilibrium affects the force and acceleration, leading to sinusoidal motion. The concept of energy in simple harmonic motion is introduced, discussing how kinetic and potential energy vary with the position of the oscillator.
📈 Graphs of Simple Harmonic Motion
This section focuses on the graphical representation of simple harmonic motion, including position vs. time, velocity vs. time, and acceleration vs. time graphs. The video instructs viewers to pause and predict what these graphs would look like for a spring oscillating horizontally. It explains how the slope of the position-time graph represents velocity and how the slope of the velocity-time graph represents acceleration. The video also discusses the changes in velocity, acceleration, and energy throughout one complete oscillation.
🌐 Factors Affecting the Period of a Pendulum
The video explores factors that affect the period of a pendulum, such as mass, amplitude, length of the string, and gravitational field strength. Experiments are shown to demonstrate that the period of a pendulum is independent of its mass and amplitude but depends on the length of the string and the gravitational field strength. The formula for the period of a pendulum is introduced and explained, highlighting the relationship between period, length, and gravitational field strength.
🔧 Factors Affecting the Period of a Spring
Similar to the pendulum, this paragraph examines the factors that influence the period of a spring oscillator, including amplitude, mass, and spring constant. Through experiments, it is shown that the amplitude does not affect the period of a spring oscillator. However, the mass and spring constant do have an impact. The video explains the relationship between the period of a spring oscillator, mass, and spring constant using the appropriate formula. Different springs with varying spring constants are tested to observe their oscillation periods.
🤔 Problem Solving in Simple Harmonic Motion
The video presents a problem-solving scenario involving a cart attached to a spring, which is part of a simple harmonic oscillator system. The scenario involves changing the displacement of the cart and observing the resulting changes in velocity over time. Viewers are asked to predict and explain the changes in the velocity graph based on the new conditions. The concept of energy transfer and momentum is introduced when a dart is shot into the cart at different times, affecting the system's maximum speed and period. The video encourages viewers to practice their physics problem-solving skills and apply their understanding of simple harmonic motion principles.
👋 Conclusion and Future Topics
Christine Gonzalez Vega concludes the video by summarizing the main points covered in the session, which include the characteristics of simple harmonic motion, the factors affecting the period of pendulums and springs, and the energy changes during oscillation. She also provides a preview of upcoming topics, which will cover rotational motion and practice problems for the AP Physics 1 exam. The video serves as a comprehensive review of simple harmonic motion, preparing students for further studies and exam practice.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Restoring Force
💡Equilibrium Position
💡Amplitude
💡Period
💡Hooke's Law
💡Energy
💡Acceleration
💡Graphs
💡Damping
💡Critical Points
Highlights
The introduction of simple harmonic motion and its comparison with other types of motion, such as a bouncing ball and a pendulum.
The three requirements for simple harmonic motion: a restoring force proportional to displacement, independence of amplitude and period, and the formation of sine or cosine graphs for position and time.
The explanation of equilibrium position and the role of restoring forces in simple harmonic motion.
The discussion on how a bouncing ball does not exhibit simple harmonic motion due to the direction of gravitational force.
The application of simple harmonic motion concepts in determining the period of a spring or pendulum and its relevance in physics problems.
The detailed analysis of the forces acting on a pendulum, including tension and gravitational forces, and how they contribute to the restoring force.
The use of free body diagrams to visualize and understand the forces in simple harmonic motion scenarios.
The relationship between the spring constant and the restoring force in a spring-mass system, as explained through Hooke's Law.
The description of the graphs for position, velocity, and acceleration in simple harmonic motion, and how they relate to each other.
The practical examples and demonstrations of simple harmonic motion with a pendulum and spring, showing the effects of displacement and amplitude.
The explanation of energy conservation in simple harmonic motion, including kinetic and potential energy at different points in the oscillation.
The impact of mass on the period of a spring oscillator, demonstrating how the period changes with different masses.
The effect of the spring constant on the period of a spring oscillator, with stiffer springs leading to shorter periods.
The examination of how the period of a pendulum is affected by the length of the string and the gravitational field strength.
The comprehensive review of the main concepts, equations, and applications of simple harmonic motion, providing a solid understanding of the topic.
Transcripts
Browse More Related Video
Simple Harmonic Motion - IB Physics

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion
Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems

2021 Live Review 3 | AP Physics C: Mechanics | Graphing Simple Harmonic Motion

Simple Harmonic Motion

Simple harmonic motion and angular frequency [IB Physics SL/HL]
5.0 / 5 (0 votes)
Thanks for rating: