Understanding Universal law of Gravitation!
TLDRThe video script explores the concept of universal gravitation, highlighting Sir Isaac Newton's pivotal role in its discovery. It begins with a demonstration of gravitational force using masses on a scale and moves on to recount Newton's insight, inspired by an apple falling from a tree, which led to the realization that Earth's attraction is radial, not just downward. Newton's observations on the moon's orbit and the apple's acceleration on Earth helped him deduce that gravitational force is inversely proportional to the square of the distance between two objects. The video also explains how Newton's third law of motion influenced the understanding that forces between two objects are equal and opposite. The script then describes how Newton formulated the equation for gravitational force, introducing the gravitational constant. It touches on the challenge of observing this force in everyday life due to friction but illustrates the concept with a hypothetical experiment. The video concludes with a mention of Henry Cavendish, who later determined the value of the gravitational constant, g, through a clever torsional balance experiment.
Takeaways
- 🌍 **Gravitational Force Universality**: Every object in the universe attracts every other object with a force that acts along a straight line towards the centers of the objects.
- 🍎 **Newton's Apple Inspiration**: Sir Isaac Newton's contemplation on why an apple falls straight down led to the discovery of the universal law of gravitation.
- 🌕 **Centripetal Force and Moon's Motion**: Newton used the moon's orbit to deduce that the gravitational force must provide the necessary centripetal force for its circular motion.
- ⚖️ **Newton's Third Law in Gravitation**: The forces of attraction between two objects are equal in magnitude and opposite in direction, as per Newton's third law of motion.
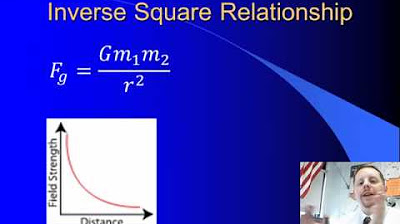
- 🔍 **Inverse Square Law**: Newton deduced that the gravitational force is inversely proportional to the square of the distance between the centers of the two objects.
- 📚 **Mass Dependency**: The force of gravitation is directly proportional to the product of the masses of the two objects involved.
- 🎓 **Newton's Law of Universal Gravitation**: Newton formulated an equation that includes a gravitational constant to quantify the gravitational force between two objects.
- 🔗 **Gravitational Constant (G)**: The value of the gravitational constant was determined by Henry Cavendish long after Newton's time, using a torsion balance experiment.
- 🧲 **Frictionless Attraction**: In a frictionless environment, objects would move towards each other due to gravitational force until they collide.
- 📐 **Cavendish Experiment**: Cavendish's experiment allowed for the measurement of the gravitational constant by balancing gravitational attraction against a known torsional force.
- 🌌 **Cosmic Interaction**: The universal law of gravitation explains the mutual attraction between all objects in the universe, from planets to stars to everyday items.
Q & A
What is the universal law of gravitation?
-The universal law of gravitation states that every object in the universe attracts every other object with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
How did Sir Isaac Newton discover the universal law of gravitation?
-Newton discovered the universal law of gravitation after observing an apple fall from a tree. He reasoned that if the Earth attracts objects radially towards its center, it must also attract the Moon and other celestial bodies in a similar manner.
What is the role of centripetal force in the motion of the Moon around the Earth?
-The centripetal force required for the Moon's circular motion is supplied by the gravitational force between the Earth and the Moon. This prevents the Moon from falling towards the Earth.
How did Newton establish the relationship between gravitational force and distance?
-Newton compared the acceleration of an apple falling near the Earth's surface with the centripetal acceleration of the Moon. He found that the gravitational force is inversely proportional to the square of the distance between the centers of the objects.
What is the significance of the gravitational constant in Newton's equation for gravitational force?
-The gravitational constant, denoted as 'G', is a proportionality constant that relates the gravitational force between two objects to the product of their masses and the square of the distance between their centers.
Who was the first to measure the gravitational constant, and how did they do it?
-Henry Cavendish was the first to measure the gravitational constant. He used a torsion balance experiment to compare the gravitational attraction between masses with the torsional force of a twisted wire.
Why do we not observe the gravitational attraction between everyday objects?
-The gravitational attraction between everyday objects is often negligible due to the small masses involved and the presence of other forces, such as friction, which can counteract the gravitational force.
How does Newton's third law of motion relate to the forces between two objects due to gravity?
-According to Newton's third law, for every action, there is an equal and opposite reaction. This means that the force with which one object attracts another is equal in magnitude and opposite in direction to the force with which the second object attracts the first.
What is the formula for calculating the force of gravity according to the universal law of gravitation?
-The formula for calculating the force of gravity (F) is F = G * (m1 * m2) / r^2, where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between the centers of the two objects.
Why does the Earth not move towards an apple when both are attracted to each other by gravity?
-The Earth does not move towards an apple because the Earth's mass is much greater than the apple's mass. When the gravitational force is divided by the Earth's mass, the resulting acceleration is negligible, making the motion imperceptible.
What is a hypothetical experiment that could demonstrate the gravitational attraction between two objects?
-A hypothetical experiment could involve placing two blocks in a long, frictionless room. If the frictional force between the objects and the floor is zero, the blocks would move towards each other due to gravitational force and eventually collide.
How can the effect of gravitational force be visualized using a hanging two-ball arrangement?
-By placing two heavy balls near a hanging two-ball arrangement, one can observe the small balls slowly moving towards and eventually touching the larger ones. This demonstrates the gravitational attraction between the masses.
Outlines
📚 Introduction to Universal Law of Gravitation
This paragraph introduces the concept of gravitational force, explaining how it acts between any two objects in the universe. It describes a demonstration involving a scale with masses and the effect of placing larger masses nearby, leading to the attraction and eventual sticking together of the smaller masses. The narrative then delves into the history of the discovery of the universal law of gravitation by Sir Isaac Newton, triggered by the observation of an apple falling from a tree. Newton's insight that the Earth attracts objects radially towards its center is highlighted, as is his realization that similar forces act between the Earth, the Moon, and the Sun. The paragraph also touches on Newton's third law of motion, which implies that the forces between two objects are equal and opposite. Finally, it outlines Newton's challenge to derive an equation to predict the magnitude of gravitational force, leading to his conclusion that this force is inversely proportional to the square of the distance between the centers of the objects involved.
🌌 The Gravitational Constant and its Impact
The second paragraph discusses the implications of the universal law of gravitation, emphasizing that all objects in the universe attract each other. It challenges the common disbelief in this concept due to the ever-present frictional forces in our daily experiences. A hypothetical scenario of a frictionless room with two blocks is presented to illustrate how, in the absence of friction, objects would move towards each other due to gravity. The paragraph then describes a more realistic experiment involving hanging balls that move towards larger, nearby balls, demonstrating gravitational attraction. The narrative shifts to the historical account of Henry Cavendish, an English scientist who first measured the gravitational constant (g) using a torsion balance experiment. Cavendish's setup allowed for a balance between gravitational force and the torsional force of the strings, enabling him to calculate the value of g. The paragraph concludes with an affirmation of the understanding of the universal law of gravitation and an anticipation of future discussions on the topic.
Mindmap
Keywords
💡Gravitational Force
💡Universal Law of Gravitation
💡Centripetal Force
💡Newton's Third Law of Motion
💡Gravitational Constant (G)
💡Inertia
💡Frictionless Environment
💡Torsional Force
💡Centripetal Acceleration
💡Mass
💡Distance
Highlights
Gravitational force acts between any two objects in the universe, demonstrating the effect by suspending a horizontal scale with two masses at the end.
Quickly placing two large masses next to the scale causes the small masses to move closer to the large masses due to gravitational force.
Isaac Newton's discovery of the universal law of gravitation was inspired by observing an apple falling from a tree.
Newton deduced that the Earth attracts objects radially towards its center, not just downward.
The moon's orbit around Earth is maintained by the balance between gravitational force and centripetal force.
Newton compared the acceleration of an apple falling on Earth with the moon's centripetal acceleration to find a connection.
Gravitational force is inversely proportional to the square of the distance between the centers of the objects.
Newton's third law of motion states that the forces between two objects are equal and opposite.
The force due to the universal law of gravitation is a factor of the masses of both objects involved.
Newton introduced the gravitational constant to form a proper equation for the universal law of gravitation.
The gravitational force between objects is independent of the object's mass when it comes to acceleration.
In a frictionless environment, objects would move towards each other due to gravitational force until they collide.
Henry Cavendish was the first to measure the gravitational constant (g) using a torsion balance experiment.
Cavendish's experiment allowed for a balance between gravitational force and the strings' torsional force to calculate g.
The universal law of gravitation states that all objects in the universe attract each other with a force that can be calculated using Newton's equation.
Objects in the universe exert a negligible acceleration when the gravitational force is divided by their mass, which is why we don't notice the attraction in everyday life.
A more realistic experiment to visualize gravitational force involves placing two heavy balls near a hanging two-ball arrangement, causing the small balls to move towards the larger ones.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: