AP Physics Workbook 3.M Gravitational Fields
TLDRThis transcript delves into the concepts of circular motion and gravitation in AP Physics, explaining the derivation of gravitational force equations and the gravitational field. It highlights Newton's law of gravitation, the calculation of gravitational force between two masses, and the impact of distance on this force. The discussion extends to comparing Earth's gravitational field with that of Mars, demonstrating how Mars' gravity is 4/10th of Earth's. The transcript also addresses the relationship between gravitational acceleration and the time it takes for an object to fall, emphasizing that a weaker gravitational pull results in a longer descent time. It clarifies misconceptions regarding the mathematical representation of these physical phenomena.
Takeaways
- 📚 The script is a lecture on AP Physics, focusing on circular motion and gravitation.
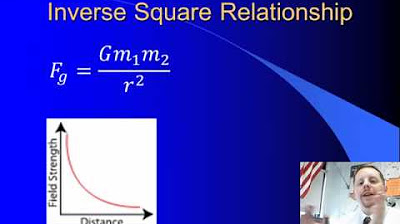
- 🌍 The gravitational force (G) is derived from Newton's law of gravitation, which states that every particle in the universe attracts every other particle with a force proportional to the product of their masses and inversely proportional to the square of the distance between them.
- 🔢 The gravitational constant (G) is approximately 9.8 m/s^2 on Earth, and it is derived from the force of gravity acting on an object due to the Earth's gravitational field.
- 🌕 The force of gravity is directly proportional to the mass of the object and inversely proportional to the square of the distance from the center of the Earth to the center of the object.
- 🪐 The gravitational field on Mars can be calculated using the same principles, with Mars having 1/10 the mass of Earth and a radius that is 1/2 that of Earth.
- 🚀 The acceleration due to gravity on Mars is approximately 4 m/s^2, which is 4/10 the acceleration due to gravity on Earth.
- 📉 The time it takes for an object to fall in a gravitational field is inversely proportional to the strength of the gravitational field.
- 🕰️ An object will take longer to fall on Mars due to its weaker gravitational field compared to Earth.
- 📈 The relationship between height and time in free-fall motion is such that an increase in height results in an increase in time taken to fall.
- 🔄 The height in the equations of motion can be in the numerator or denominator, affecting the relationship between height and time.
- 🧠 Understanding the relationship between gravitational force, mass, distance, and acceleration is crucial for solving problems in physics related to circular motion and gravitation.
Q & A
What is the source of the 9.8 m/s^2 gravitational acceleration felt on Earth?
-The 9.8 m/s^2 gravitational acceleration is derived from the gravitational field, which is a result of the force exerted by the Earth on objects due to gravity.
How did Newton determine the relationship between gravity and mass?
-Newton realized that the force of gravity on an object depends not only on the distance but also on the object's mass. It is directly proportional to the mass, as per Newton's third law, which states that every action has an equal and opposite reaction.
What is the universal law of gravitation as described by Newton?
-The universal law of gravitation states that every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
What is the formula for calculating the gravitational force?
-The formula for calculating the gravitational force is F = G * (mass1 * mass2) / R^2, where F is the gravitational force, G is the gravitational constant, mass1 and mass2 are the masses of the objects, and R is the distance between their centers.
How does the gravitational field on Mars compare to that on Earth?
-The gravitational field on Mars is weaker than on Earth. Mars has 1/10 the mass of Earth and its radius is 1/2 that of Earth, which results in a gravitational acceleration on Mars that is approximately 4/10 of that on Earth.
What is the approximate acceleration due to gravity on the surface of Mars?
-The approximate acceleration due to gravity on the surface of Mars is about 4 meters per second squared, which is less than the 9.8 m/s^2 experienced on Earth.
How does the gravitational acceleration affect the time it takes for an object to fall?
-The greater the gravitational acceleration, the shorter the time it takes for an object to fall a given distance. Conversely, a weaker gravitational acceleration, like that on Mars, results in a longer fall time for the same distance.
What is the relationship between height and time in the context of free-fall?
-In free-fall, the height from which an object falls is directly proportional to the square of the time it takes to fall, assuming no air resistance and a constant acceleration due to gravity.
Why does the equation T = √(2gh) suggest that increasing height results in increasing time?
-The equation T = √(2gh) shows that time (T) is directly proportional to the square root of the height (h). This means that as the height increases, the time required for an object to fall that distance also increases, because the object has to cover more distance under the influence of gravity.
How does the position of height in an equation affect the relationship between height and time?
-The position of height in an equation determines whether it is directly or inversely proportional to time. If height is in the numerator, it is directly proportional to time, but if height is in the denominator, it is inversely proportional to time, meaning an increase in height would result in a decrease in time, which is not the case for free-falling objects.
What is the significance of the gravitational constant (G) in the formula for gravitational force?
-The gravitational constant (G) is a fundamental physical constant that couples the masses of two objects to the force between them. It is essential in calculating the exact strength of the gravitational force between two objects and is used in the universal law of gravitation.
Outlines
📚 Introduction to Gravitational Field and Newton's Law
This paragraph introduces the concept of gravitational field and its relation to the acceleration due to gravity, specifically the 9.8 m/s^2 experienced on Earth. It explains Newton's law of gravitation, which states that every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The paragraph also discusses how the force of gravity is dependent on both the mass of the Earth and the mass of the object, as well as the distance from the center of the Earth to the center of the object.
🪐 Mars' Gravitational Field and its Comparison to Earth
The second paragraph delves into the specifics of Mars' gravitational field compared to Earth's. It explains how the mass of Mars is one-tenth of Earth's mass and its radius is half that of Earth's. Using these values, the paragraph derives the acceleration due to gravity on Mars' surface, which is approximately 4 m/s^2. This is significantly less than Earth's 9.8 m/s^2, meaning that objects on Mars would experience weaker gravitational pull and would take longer to fall from the same height due to the reduced acceleration.
🚀 Impact of Gravitational Acceleration on Falling Objects
This paragraph discusses the effect of gravitational acceleration on the time it takes for an object to fall. It uses Earth and Mars as examples to illustrate that with weaker gravitational acceleration, such as on Mars, it will take longer for an object to fall the same vertical distance compared to Earth. The explanation includes a comparison of the time it would take for an object to fall from a certain height on both planets, highlighting the relationship between gravitational acceleration and the time of fall.
🧠 Understanding the Relationship between Height and Time in Gravitational Equations
The final paragraph addresses the mathematical relationship between height, time, and gravitational acceleration in the context of falling objects. It clarifies the misconception that increasing height in the denominator of a certain equation would decrease the time, which is incorrect. The paragraph emphasizes that when height increases, the time required for an object to fall also increases because there is more distance to cover, and this is independent of whether the height is in the numerator or denominator of the equation.
Mindmap
Keywords
💡Circular Motion
💡Gravitation
💡Gravitational Field
💡Newton's Laws
💡Gravitational Constant (G)
💡Acceleration Due to Gravity
💡Mass
💡Distance
💡Celestial Bodies
💡Free Fall
💡Vertical Displacement
Highlights
Derivation of the equation for gravitational force begins with Newton's law, which states that the force of gravity depends on both the distance and the mass of the objects involved.
According to Newton's third law, every action has an equal and opposite reaction, which applies to the gravitational forces between two objects.
The gravitational force is proportional to the product of the two masses and inversely proportional to the square of the distance between them.
The gravitational constant (G) is a key factor in the equation for the force of gravity, and it is used to calculate the force between two masses.
The concept of the gravitational field is introduced as a way to describe the influence of a massive object on its surroundings.
The acceleration due to gravity (g) is explained as a result of the gravitational field acting on an object.
The derivation of the gravitational field equation for Mars is discussed, taking into account its mass and radius compared to Earth's.
It is calculated that the acceleration due to gravity on Mars is approximately 4 meters per second squared, which is less than Earth's 9.8 m/s^2.
The impact of gravitational force on the time it takes for an object to fall is explained, with a weaker gravitational force leading to a longer fall time.
A comparison between the fall time of an object on Earth and Mars is made, highlighting the differences due to their respective gravitational fields.
The relationship between height and time in the context of gravitational force is explored, with an increase in height leading to an increase in fall time.
A formula for the time of fall is presented, with height being directly proportional to the square root of the time.
The importance of understanding the relationship between height and time in various gravitational fields is emphasized for practical applications.
An incorrect statement regarding the relationship between height and time in a specific equation is identified and corrected.
The concept that increasing height (vertical displacement) requires more time for an object to fall is reinforced as a fundamental principle.
The mathematical treatment of the relationship between height, time, and gravitational force is detailed, providing a comprehensive understanding of the underlying physics.
The practical implications of the differences in gravitational fields on planetary bodies are discussed, with Mars being used as a specific example.
The transcript concludes with a clear explanation of the key concepts and equations related to gravitational force and fields, providing a solid foundation for further study.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: