Regents Physics: Horizontal Projectile Problem Practice

Dan Fullerton
22 Oct 201112:49
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explores various horizontal projectile motion problems, including a tiger leaping from a cliff, a seagull dropping a clam, and a coyote running off a cliff, among others. It delves into the physics of motion, using equations like V = VI + at and D = Vi*t + 0.5*a*t^2 to calculate time and distance. The script emphasizes understanding the separate horizontal and vertical components of motion and how they interact, ultimately guiding viewers through the calculations to solve for different scenarios.

Takeaways
  • 🐯 In the horizontal projectile problem, a tiger leaps from a 7.5-meter high rock at 4.5 m/s horizontally and lands approximately 5.4 meters away from the base of the rock.
  • πŸ•ŠοΈ A seagull flying at a constant speed of 2.7 m/s drops a clam which lands 2.1 seconds later on a rocky beach. The clam's horizontal velocity remains the same as the seagull's, and its final vertical velocity just before impact is approximately 20.6 m/s.
  • πŸ¦… Wiley Coyote runs off a cliff at 12 m/s and strikes the ground with a total velocity of 45.9 m/s, composed of a 12 m/s horizontal velocity and a 44.3 m/s vertical velocity.
  • πŸš€ When Wiley Coyote is launched at 120 m/s from a cannon and falls from a 100-meter cliff, his final velocity remains the same in both horizontal and vertical components, resulting in a total velocity of approximately 28 m/s upon impact.
  • πŸ’£ An F-16 releases a bomb horizontally at 300 m/s from an altitude of 8 km. The bomb travels 12.1 km horizontally before striking the ground, calculated using the time it takes to fall vertically and the constant horizontal velocity.
  • πŸ“ The key to solving projectile problems is to analyze both the horizontal and vertical components separately, recognizing that the horizontal velocity remains constant and only the vertical component is affected by gravity.
  • πŸ•’ The time of flight is crucial in determining the horizontal distance in projectile problems, as it is the common factor between the horizontal and vertical motion.
  • πŸ”’ The use of kinematic equations is essential for finding unknown variables in projectile motion, such as time, displacement, and final velocities.
  • 🌐 Neglecting air resistance simplifies the projectile problems, allowing for the application of basic kinematic principles without additional complexities.
  • πŸ”„ The horizontal and vertical components of motion are independent in projectile problems, but their combination is necessary to find the resultant or total velocity.
  • πŸ“ˆ The Pythagorean theorem is used to calculate the resultant velocity when combining horizontal and vertical components of motion in projectile problems.
Q & A

  • What is the initial speed of the tiger in the horizontal projectile problem?

    -The initial speed of the tiger in the horizontal projectile problem is 4.5 meters per second.

  • How high is the rock from which the tiger leaps?

    -The rock from which the tiger leaps is 7.5 meters high.

  • What is the formula used to calculate the time of flight in the vertical direction?

    -The formula used to calculate the time of flight in the vertical direction is T = √(2D/a), where D is the displacement and a is the acceleration due to gravity (9.81 m/s^2).

  • What is the horizontal distance the tiger lands from the base of the rock?

    -The tiger lands approximately 5.4 meters from the base of the rock.

  • How long does it take for the clam dropped by the seagull to hit the ground?

    -It takes 2.1 seconds for the clam to hit the ground after being dropped by the seagull.

  • What is the final vertical velocity of the clam just before it hits the ground?

    -The final vertical velocity of the clam just before it hits the ground is approximately 20.6 meters per second.

  • How does increasing the seagull's speed affect the horizontal distance the clam travels before hitting the ground?

    -Increasing the seagull's speed increases the horizontal distance the clam travels before hitting the ground, but it does not affect the vertical velocity of the clam.

  • What is the total velocity of the coyote just before he hits the ground when running off a 100-meter cliff at 12 meters per second?

    -The total velocity of the coyote just before he hits the ground is approximately 45.9 meters per second.

  • What is the horizontal and vertical velocity of the coyote when he strikes the ground after being launched with a cannon at 120 meters per second?

    -The horizontal velocity of the coyote is 120 meters per second, and the vertical velocity is 44.3 meters per second when he strikes the ground.

  • How far does the bomb travel horizontally before striking the ground when released from an F-16 flying at 300 meters per second and an altitude of 8 kilometers?

    -The bomb travels approximately 12.1 kilometers horizontally before striking the ground.

  • What is the time it takes for the bomb released from an F-16 to hit the ground?

    -The time it takes for the bomb to hit the ground is approximately 40.4 seconds.

  • What is the key to solving horizontal projectile problems?

    -The key to solving horizontal projectile problems is separating the horizontal and vertical motions, recognizing that the time of flight is the same for both directions, and applying the appropriate kinematic equations for each direction.

Outlines
00:00
🐯 Horizontal Projectile Motion - Tiger Leap

This paragraph discusses a horizontal projectile problem involving a tiger leaping from a 7.5-meter high rock with an initial speed of 4.5 meters per second. The goal is to calculate the distance from the base of the rock where the tiger will land. The problem is approached by analyzing both horizontal and vertical motion separately. Horizontally, the tiger's speed remains constant with no acceleration, allowing for the use of the formula V_average = V_initial and the equation D = V_average * T to find the distance. Vertically, the tiger's initial speed is zero, and the displacement is 7.5 meters downward. The acceleration due to gravity is 9.81 m/s^2, and the time (T) is determined by using the formula V = V_initial + a*t, leading to T = √(2*D/a). With the time calculated, the horizontal distance (D) is found by substituting T back into the horizontal equation, resulting in approximately 5.4 meters from the base of the rock.

05:04
πŸ•ŠοΈ Projectile Motion with Speed Change - Seagull and Clam

The second paragraph examines the effect of increasing the seagull's speed on the projectile motion of a clam it drops. It is explained that the horizontal velocity of the clam will increase proportionally with the seagull's speed, while the vertical velocity will remain unchanged, neglecting air resistance. The paragraph also explores a scenario where the coyote runs off a cliff with a horizontal velocity of 12 meters per second and calculates the impact velocity by considering both horizontal and vertical components. The resultant velocity is found using vector addition, leading to a total velocity of 45.9 meters per second just before impact. A similar analysis is conducted for the coyote running off the cliff at 120 meters per second, resulting in a total velocity of approximately 141.4 meters per second.

10:07
πŸ’£ Projectile Motion with Altitude - Bomb Drop

This paragraph focuses on calculating the horizontal distance a bomb will travel before hitting the ground when dropped from an F-16 flying at 300 meters per second at an altitude of 8 kilometers. The bomb's horizontal velocity matches the plane's release velocity, and the goal is to determine the horizontal distance traveled. The vertical motion is analyzed to find the time the bomb is in the air, using the displacement of 8,000 meters and the acceleration due to gravity. The time (T) is calculated using the formula T = √(2*D/a), and the horizontal distance (D) is found by multiplying the horizontal velocity by the time, resulting in a total horizontal displacement of 12.1 kilometers.

Mindmap
Keywords
πŸ’‘Horizontal projectile motion
Horizontal projectile motion refers to the movement of an object that is launched with a certain horizontal velocity and is acted upon by gravity, causing it to follow a parabolic trajectory. In the video, this concept is central to understanding how the tiger leaps from the rock and how the bomb is released from the plane, as both move horizontally without any additional horizontal acceleration.
πŸ’‘Velocity
Velocity is a vector quantity that describes the speed of an object in a specific direction. It is crucial in determining how fast an object is moving and in which direction. In the context of the video, both horizontal and vertical components of velocity are calculated to understand the motion of the tiger, the clam, and the bomb.
πŸ’‘Acceleration due to gravity
Acceleration due to gravity is the constant rate at which objects near the Earth's surface accelerate downward when in free fall. It is approximately 9.81 m/s^2 and affects the vertical motion of objects. In the video, this acceleration is used to calculate the time it takes for the objects to hit the ground and their final vertical velocities.
πŸ’‘Time of flight
Time of flight refers to the duration an object is in motion from the point of release to the point of impact or rest. It is a key factor in projectile motion problems, as it allows the calculation of distances traveled and final velocities. The video uses time of flight to solve for the distances the tiger and the bomb travel horizontally and the clam and the coyote fall vertically.
πŸ’‘Displacement
Displacement is the change in position of an object and is typically represented as a vector from the initial to the final position. In the context of the video, displacement is used to describe the vertical distance fallen by objects and the horizontal distance traveled by projectiles.
πŸ’‘Kinematic equations
Kinematic equations are mathematical formulas used to describe the motion of objects without considering the forces that cause the motion. They relate displacement, velocity, acceleration, and time. In the video, kinematic equations are essential for solving the projectile motion problems, such as finding the time of flight and the horizontal distance traveled.
πŸ’‘Projectile motion
Projectile motion is a type of motion where an object is launched into the air with an initial velocity and is influenced only by gravity. It involves separating the motion into horizontal and vertical components. The video focuses on solving problems related to projectile motion, such as calculating distances and velocities of leaping animals and falling objects.
πŸ’‘Free fall
Free fall is the motion of an object falling under the sole influence of gravity, starting from rest, and without any air resistance. It is a specific case of projectile motion where the only acceleration is vertical. The video uses the concept of free fall to determine the time it takes for the clam and the coyote to reach the ground and their final velocities.
πŸ’‘Resultant velocity
Resultant velocity is the overall velocity of an object moving with constant velocity in two or more directions simultaneously. It is found by combining the individual component velocities using vector addition. In the video, resultant velocities are calculated for the coyote and the bomb to understand their total speed and direction just before impact.
πŸ’‘Vector addition
Vector addition is the process of combining two or more vectors to find a single resultant vector. It is used when dealing with motion in multiple directions at once. In the video, vector addition is used to calculate the total velocity of the bomb and the coyote by combining their horizontal and vertical velocity components.
πŸ’‘Parabolic trajectory
A parabolic trajectory is the path followed by an object in projectile motion, which is a curve shaped like a parabola due to the combination of constant horizontal velocity and accelerating motion under gravity. In the video, the parabolic trajectory is the shape of the path taken by the leaping tiger, the falling clam, and the bomb in flight.
Highlights

The tiger leaps horizontally from a 7.5-meter high rock with a speed of 4.5 m/s.

The problem is a projectile motion problem, which requires analyzing both horizontal and vertical directions.

In the horizontal direction, there is no acceleration due to gravity, so the average speed can be used to calculate distance.

The vertical motion is affected by gravity, and the standard kinematic equation can be applied to find the time of flight.

The time of flight for the tiger is calculated to be approximately 1.2 seconds using the vertical displacement and acceleration due to gravity.

The horizontal distance the tiger lands from the base of the rock is roughly 5.4 meters, calculated using the horizontal speed and time of flight.

The seagull flies horizontally at a constant speed of 2.7 m/s and releases a clam, which lands on the beach 2.1 seconds later.

The clam maintains the same horizontal velocity as the seagull due to the lack of horizontal acceleration.

The vertical velocity of the clam just before it hits the ground is determined to be approximately 20.6 m/s.

If the seagull's speed increases, the horizontal distance the clam travels will also increase, but the vertical velocity will remain unchanged.

Wile E. Coyote runs off a 100-meter cliff with a horizontal velocity of 12 m/s and strikes the ground with a total velocity of 45.9 m/s.

The coyote's horizontal velocity remains constant at 12 m/s, while the vertical velocity is calculated to be 40.3 m/s just before impact.

When Wile E. Coyote's speed is increased to 120 m/s, the horizontal and vertical velocities remain the same, and the total velocity just before impact is approximately 127 m/s.

An F-16 flying horizontally at 300 m/s releases a bomb from an altitude of 8 km, and the bomb's horizontal travel distance is calculated to be 12.1 km.

The bomb maintains the same horizontal velocity as the plane, and its vertical motion is analyzed to determine the time in the air.

The time the bomb is in the air is approximately 40.4 seconds, derived from the vertical displacement and acceleration due to gravity.

Key to solving these problems is separating the horizontal and vertical components and recognizing that time is the common factor.

Transcripts

Browse More Related Video

Horizontally launched projectile | Two-dimensional motion | Physics | Khan Academy

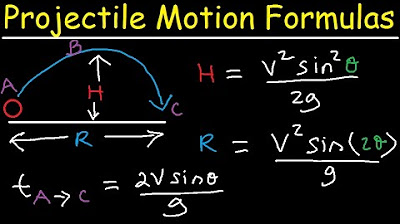
Introduction to Projectile Motion - Formulas and Equations

How To Solve Any Projectile Motion Problem (The Toolbox Method)

Projectile Launched of a Cliff

Kinematics Part 3: Projectile Motion

Physics 3.5.4a - Projectile Practice Problem 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsProblemsProjectileMotionKinematicsLeverageGravityTigerLeapSeagullFlightCoyoteChaseMotionAnalysisEducationalContentScienceExploration