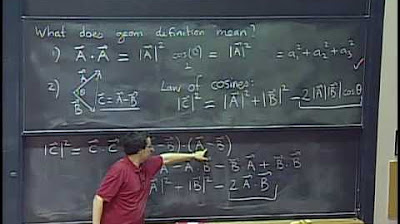High School Physics: Vectors and Scalars
TLDRIn this informative video, Dan Fullerton explores the concepts of vectors and scalars, focusing on their differences and how to manipulate vectors using diagrams. He explains the process of determining vector components and angles, and how to calculate the resultant vector through addition and equilibrant vector through subtraction. The video also covers real-world applications, such as calculating the components of a soccer ball's velocity and an airplane's eastward velocity, and concludes with a practical exercise for viewers to apply these concepts in their own environment.
Takeaways
- 📏 Vectors and Scalars: Scalars are physical quantities with only magnitude, like temperature, mass, and time. Vectors have both magnitude and direction, such as velocity, force, and momentum.
- 🔽 Vector Representation: Vectors are typically represented by arrows in physics, where the arrow's direction indicates the vector's direction and its length represents the magnitude.
- 📐 Measuring Vectors: The length of a vector can be measured to determine its magnitude, and the ratio of the vector's length to a known unit can be used to find the force or other physical quantities it represents.
- 🤝 Vector Addition: Vectors can be added graphically by aligning them tip-to-tail and drawing a line from the start of the first vector to the end of the last to find the resultant vector.
- 🔄 Vector Subtraction: To subtract a vector, reverse its direction and add it to the original vector, effectively switching the order of addition.
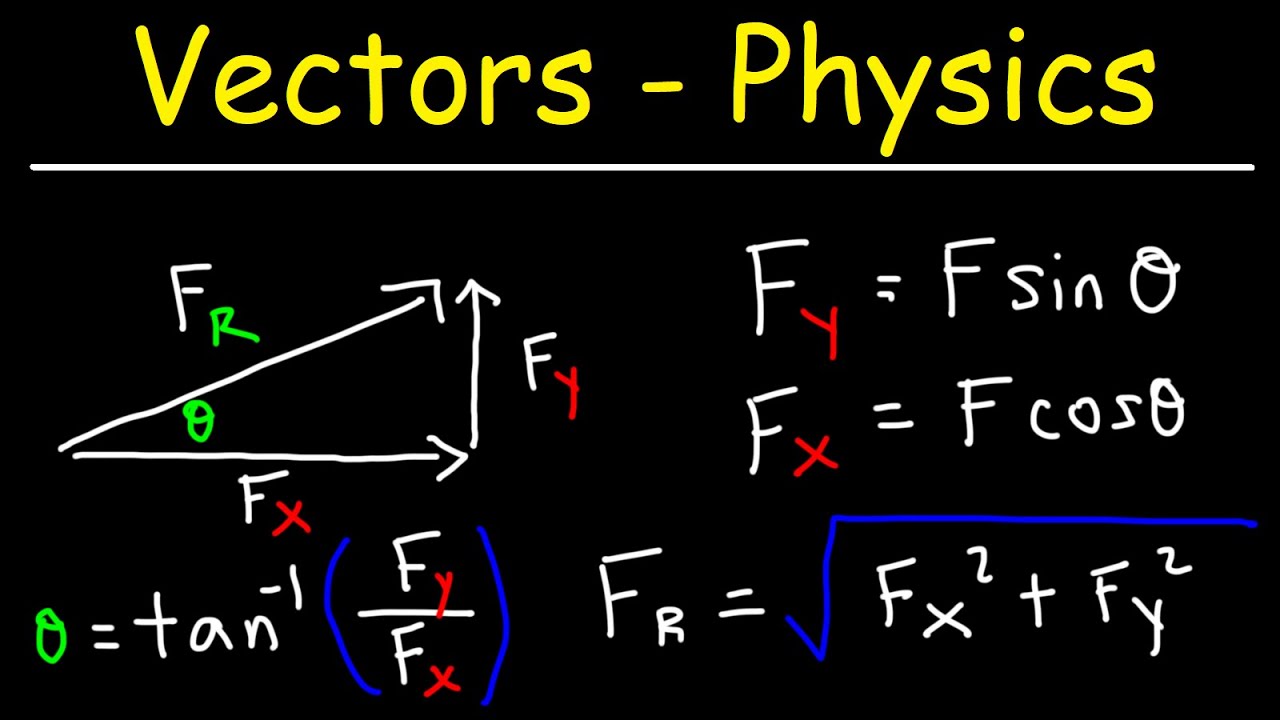
- 📊 Components of Vectors: Vectors can be broken down into their X and Y components using trigonometry. The X component is found using the cosine of the angle (adjacent side), and the Y component using the sine (opposite side).
- 🔄 Finding the Angle: Given the X and Y components of a vector, the angle can be determined using the inverse tangent (arctangent) of the Y component divided by the X component.
- 🏀 Real-world Applications: The concepts of vectors and their components can be applied to real-world scenarios, such as finding the horizontal and vertical components of a soccer ball's velocity or an airplane's eastward velocity.
- 📈 Equilibrium Vector: The equilibrium vector is the opposite of the resultant vector and can be found by reversing the direction of the resultant.
- 🌐 Vectors in Different Scenarios: Understanding vectors and their manipulation is crucial in various fields, including physics, engineering, and more, for analyzing and solving problems involving motion and forces.
- 💡 Practice and Experimentation: To solidify understanding, one can define a starting and ending point and find three vectors that, when followed, lead to the endpoint, reinforcing the concepts of vector addition and resultant vectors.
Q & A
What are scalar quantities?
-Scalars are physical quantities that have a magnitude or size only, without any direction. Examples include temperature, mass, and time.
How are vectors different from scalars?
-Vectors are quantities that have both magnitude and direction, unlike scalars which have only magnitude. Examples of vectors include velocity, force, and momentum.
How is the magnitude of a vector represented in diagrams?
-The magnitude of a vector is represented by the length of the arrow in diagrams, with the direction of the arrow indicating the direction of the vector.
What is the process of adding two vectors graphically?
-To add two vectors graphically, you align them tip-to-tail, then draw a line from the starting point of the first vector to the ending point of the last vector to get the resultant vector.
How can you find the X and Y components of a vector?
-The X and Y components of a vector can be found using trigonometry. The X component is equal to the vector's magnitude times the cosine of the angle (theta), and the Y component is equal to the vector's magnitude times the sine of the angle (theta).
If you know the X and Y components of a vector, how can you find the angle between the vector and the horizontal axis?
-If you know the X and Y components (ax and ay) of a vector, you can find the angle (theta) using the tangent function: tan(theta) = ay / ax, and then find the angle by taking the inverse tangent (arctangent) of this ratio.
How do you graphically subtract one vector from another?
-To graphically subtract one vector from another, you switch the direction of the vector you are subtracting, effectively making it a negative, and then add it to the first vector following the same tip-to-tail method used for addition.
What is the equilibrant vector and how do you find it?
-The equilibrant vector is the vector that is equal in magnitude but opposite in direction to the resultant vector. To find it, first determine the resultant vector, then simply reverse its direction.
How can you verify the components of a vector using the Pythagorean theorem?
-You can verify the components of a vector by using the Pythagorean theorem, which states that the square of the hypotenuse (the resultant vector) is equal to the sum of the squares of the other two sides (the components). If the components are correct, the square root of the sum should equal the magnitude of the vector.
What is the significance of finding the resultant vector in physics?
-Finding the resultant vector is significant in physics as it allows us to understand the net effect of multiple forces or movements acting on an object. It simplifies the analysis of complex situations by reducing them to a single, equivalent vector.
Can you provide an example of how to find the magnitude of a vector given its components?
-Yes, if you have a vector with components (ax, ay), you can find its magnitude using the Pythagorean theorem: magnitude = sqrt(ax^2 + ay^2). This gives you the length of the hypotenuse, which represents the magnitude of the vector.
Outlines
📐 Introduction to Vectors and Scalars
This paragraph introduces the concepts of vectors and scalars, highlighting the differences between them. Scalars are physical quantities with only magnitude, such as temperature, mass, and time. Vectors, on the other hand, have both magnitude and direction, like velocity, force, and momentum. The paragraph explains how vectors are represented in physics using arrows, where the arrow's direction indicates the vector's direction and its length represents the magnitude. It also introduces the basic process of adding vectors graphically by aligning them tip-to-tail and drawing a line from the starting point of the first vector to the ending point of the last to find the resultant vector. The concept of vector magnitude and how it relates to the length of the arrow is also discussed, along with a method for determining the force a vector represents based on its length.
📐 Vector Addition and Subtraction
This paragraph delves into the processes of vector addition and subtraction. It explains how to add vectors by aligning them tip-to-tail and then drawing a line from the starting point of the first vector to the endpoint of the last, resulting in the resultant vector. The paragraph also covers vector subtraction, which involves changing the direction of the vector being subtracted and then adding it to the original vector. The concept of components of a vector is introduced, explaining how a vector can be broken down into its X and Y components using trigonometry. The example of a soccer ball kicked at an angle is used to illustrate how to find the horizontal and vertical components of a vector's velocity.
📐 Vector Components and Equilibrium
This paragraph focuses on the concept of vector components and the application of trigonometry to find them. It explains how a vector can be decomposed into components along the X and Y axes and how these components can be used to simplify problems in physics. The example of an airplane flying at an angle is used to demonstrate how to find the eastward component of its velocity. The paragraph also introduces the concept of the resultant vector, which is the sum of all vectors, and the equilibrant vector, which is the opposite of the resultant vector. The equilibrant vector is used to illustrate the balance of forces in concurrent force situations. The paragraph concludes with a practical activity where the listener is encouraged to find three vectors that will take them from a starting point to an ending point in their yard or house, emphasizing the importance of understanding vector addition and the relationship between vectors and their components.
Mindmap
Keywords
💡Vectors
💡Scalars
💡Magnitude
💡Direction
💡Components
💡Trigonometry
💡Resultant Vector
💡Equilibrant Vector
💡Vector Addition
💡Vector Subtraction
💡Pythagorean Theorem
Highlights
Introduction to the concepts of vectors and scalars, emphasizing their differences in terms of magnitude and direction.
Explanation of scalar quantities such as temperature, mass, and time, which possess only magnitude without direction.
Definition of vectors as physical quantities with both magnitude and direction, using examples like velocity, force, and momentum.
Representation of vectors using arrows in physics, where the arrow's direction indicates the vector's direction and its length represents magnitude.
Description of how to determine the magnitude of a vector using a scale diagram, relating the vector's length to its quantitative value.
Process of adding vectors graphically by aligning them tip-to-tail and drawing a line from the starting point of the first to the ending point of the last vector.
Explanation of vector subtraction as a variation of addition, where the direction of one vector is reversed to achieve the desired result.
Introduction to the concept of vector components, breaking down a vector into its X and Y components using trigonometry.
Method for calculating the X and Y components of a vector using the cosine and sine of the angle theta with respect to the horizontal axis.
Practical example of finding the horizontal and vertical components of a soccer ball's velocity, given its initial velocity and angle above the horizontal.
Application of vector concepts to determine the eastward velocity of an airplane flying at a certain speed and angle south of east.
Calculation of a dog's total displacement by considering the vector addition of its movements north and east.
Discussion of the resultant vector as the sum of multiple vectors and the concept of the equilibrant vector as the opposite of the resultant.
Activity suggestion for finding three vectors that can transport one from a starting to an ending point, emphasizing the importance of vector direction and magnitude.
Advice for using the Pythagorean theorem to calculate the magnitude of vectors in a right-angled triangle setup.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: