AP Physics Workbook 4.G Circular Motion Forces and Energy
TLDRThe transcript discusses a physics problem involving a toy car on a track with a loop-de-loop, emphasizing the conservation of energy and the forces at play. It explains that the car's release height must be greater than the loop's diameter for it to complete the circuit, as the energy must be sufficient for both potential and kinetic requirements. The video also critiques an equation proposed by Carlos, highlighting the inconsistency between the equation's prediction and the actual physical behavior, as well as a unit discrepancy. Finally, it predicts the outcome of releasing the car from a height of 0.8 meters, suggesting that it would not complete the loop due to insufficient normal force.
Takeaways
- 📚 The scenario involves a toy car moving on a track with a loop-de-loop, where it's released from rest and doesn't lose contact with the track.
- 🌐 The system considered includes the car and Earth, with rotational effects from the wheel, friction, and air resistance ignored.
- ⚙️ The roller coaster example is used to illustrate the conservation of energy, where energy remains constant at all points of the ride.
- 📈 At the start, the car has all potential energy (MGH) and no kinetic energy, which changes as it descends and gains speed.
- 🔄 The energy at the bottom of the track is a combination of potential (MGH) and kinetic energy (1/2 MV^2).
- 🚂 The height (Y) the roller coaster needs to reach is directly related to the energy it has; more energy is required for greater heights.
- 🎢 The car will not complete the loop if the release height is less than the diameter of the loop due to insufficient kinetic energy.
- 💫 The forces acting on the car during circular motion include gravity pulling it down and the normal force acting perpendicular to the surface.
- 📊 A line of best fit should be a straight line with an equal number of points above and below it, representing the relationship between variables.
- 🔧 The equation provided by Carlos is incorrect because it suggests a direct relationship between the normal force and height, whereas there should be an inverse relationship.
- 📌 The units in Carlos's equation do not match, as the left side is in Newtons (a force unit) and the right side should also be in Newtons, but it incorrectly results in a unit of kilograms per second squared.
Q & A
What is the main concept discussed in the transcript?
-The main concept discussed in the transcript is the application of the conservation of energy principle in the context of a roller coaster scenario, specifically focusing on the transformation between potential and kinetic energy.
How does the height of the roller coaster affect its energy at the bottom part?
-At the bottom part of the roller coaster, all the energy is potential energy, which is equal to the product of the mass, gravitational acceleration, and the height (MGH). The higher the roller coaster, the more potential energy it has at the bottom.
What happens to the energy at the top of the loop in the roller coaster?
-At the top of the loop, the roller coaster has both potential and kinetic energy. The potential energy is given by MGH, and the kinetic energy is given by 0.5 * M * V^2, where V is the velocity of the roller coaster at that point.
Why is it necessary for the release height of the roller coaster to be greater than the diameter of the loop?
-The release height must be greater than the diameter of the loop to ensure that the roller coaster has enough potential energy to convert into kinetic energy to complete the loop. If the height is equal to or less than the diameter, the roller coaster will not have sufficient energy to make it around the loop.
What is the significance of the centripetal force in the scenario described?
-The centripetal force is essential for keeping the roller coaster on its circular path. It acts towards the center of the circle and is a result of the combination of gravitational force and the normal force exerted by the track on the roller coaster.
How does the energy chart help in understanding the roller coaster's motion?
-The energy chart helps visualize the distribution of potential and kinetic energy at different points of the roller coaster's motion. It shows how potential energy is converted into kinetic energy and vice versa, allowing us to predict the roller coaster's behavior at various stages of the ride.
What is the relationship between the normal force and the height in Carlos's equation?
-In Carlos's equation, the normal force has an inverse relationship with the height. As the height (H) increases, the normal force (F_N) should decrease, because H is in the denominator of the equation F_N = 2 * MG / H.
Why is the slope of the line of best fit in the graph related to the units of the equation?
-The slope of the line of best fit is related to the units because it reflects the relationship between the variables in the equation. If the units do not match on both sides of the equation, the graph will not be a straight line, and the slope will not accurately represent the relationship.
What would happen if the roller coaster is released from a height of 0.8 meters?
-If the roller coaster is released from a height of 0.8 meters, it will not complete the loop. According to the line of best fit, a height of 0.8 meters would produce a negative normal force, which is not physically possible. The roller coaster would get stuck in the middle of the loop.
How does the conservation of energy principle apply to the roller coaster?
-The conservation of energy principle states that energy cannot be created or destroyed, only transformed from one form to another. In the roller coaster, potential energy is converted to kinetic energy and vice versa. At every point in the ride, the total amount of energy remains constant, although its forms may change.
What is the role of friction and air resistance in the roller coaster scenario?
-Friction and air resistance are considered negligible in this idealized roller coaster scenario. This simplification allows for easier analysis of the energy transformations without the complicating factors of energy loss due to these resistive forces.
Outlines
📚 Introduction to Energy Conservation in Physics
This paragraph introduces the concept of energy conservation in the context of a toy car moving through a loop-de-loop scenario. It emphasizes the importance of understanding how potential and kinetic energy interact within a system, such as the car and Earth, where friction and air resistance are negligible. The roller coaster analogy is used to illustrate how energy remains constant at different points, with potential energy being converted into kinetic energy as the roller coaster moves through its course. The paragraph sets the stage for a deeper analysis of forces and energy transformations in the subsequent sections.
🔧 Analyzing the Roller Coaster's Energy Requirements
This section delves into the specifics of the roller coaster's energy requirements to complete a loop. It explains why the initial height (H) must be greater than the diameter of the loop for the roller coaster to successfully navigate the full circuit. The explanation is grounded in the conservation of energy, highlighting the need for sufficient potential energy at the peak to maintain the kinetic energy required to overcome the loop's gravitational pull. The paragraph also clarifies the relationship between the heights of different points on the track and the corresponding energy values, reinforcing the concept that energy must be conserved throughout the system.
📉 Critiquing Carlos's Equation and Its Graphical Representation
The focus of this paragraph is on critiquing Carlos's equation, which describes the relationship between the normal force and the height. It points out the discrepancy between the equation's implication of an inverse relationship and the actual graph's positive slope, indicating a direct relationship. The critique is based on the principle that as height increases, the normal force should decrease, which is contrary to what the graph suggests. Additionally, the paragraph highlights a unit inconsistency in the equation, where the left side is in Newtons, but the right side should be in kilograms per second squared after canceling out the meter from the height. Lastly, it explores the scenario of releasing the car from a height of 0.8 meters and predicts that the car would not complete the loop due to the normal force becoming zero, causing the car to stall mid-loop.
Mindmap
Keywords
💡Conservation of Energy
💡Potential Energy
💡Kinetic Energy
💡Centripetal Force
💡Normal Force
💡Loop-de-Loop
💡Friction
💡Energy Chart
💡Line of Best Fit
💡Carlos's Equation
💡Unit Analysis
Highlights
The scenario involves a toy car released from rest on a track with a loop-de-loop, focusing on the conservation of energy and the forces involved.
The system under consideration includes the car and Earth, with rotational effects from the wheel and friction and air resistance being negligible.
The energy conservation principle is applied to a roller coaster, with an arbitrary energy value of 10 joules used for illustration.
At the bottom of the track, all the energy is potential (10 joules), equal to MGH, with no kinetic energy.
At the top of the roller coaster, the energy comprises both potential and kinetic, with the height (Y) being critical for the car to complete the loop.
The car will not complete the loop if the release height is less than the diameter of the loop, as it does not have enough potential energy to convert to kinetic energy.
Centripetal force is introduced as the force pulling the car towards the center of the circular motion.
The energy chart is filled in to represent the initial and final states of the car's energy, distinguishing between potential and kinetic energy.
The bar explanation clarifies why the release height must be greater than the loop's diameter to ensure the car completes the loop.
The line of best fit for a set of data should be a straight line with an equal number of points above and below it.
Carlos's equation is inconsistent with the graph because it suggests an inverse relationship between the normal force and height, which contradicts the graph's positive slope.
The units in Carlos's equation do not match, as the left side is in Newtons while the right side should be in kilograms per second squared after dimension analysis.
The normal force cannot be negative; if it were, the car would not complete the loop and would get stuck in the middle.
If the car is released from a height of 0.8 meters, it will not complete the loop as the normal force would be zero at that height, causing it to get stuck in the middle of the loop.
The car will complete the loop if released from a height greater than 1 meter, as indicated by the positive normal force values on the graph.
The conservation of energy principle is crucial for understanding the car's motion on the roller coaster and its ability to complete the loop.
The problem-solving approach involves analyzing the forces, calculating energy, and applying physical principles to predict the car's motion and the effects of different heights.
Transcripts
Browse More Related Video
Loop-the-loop physics problem: Forces on a vertical loop.

Conservation of Energy

Capacitors and Kirchhoff: Crash Course Physics #31
5 Examples of Solving Centripetal Force Problems - IB Physics
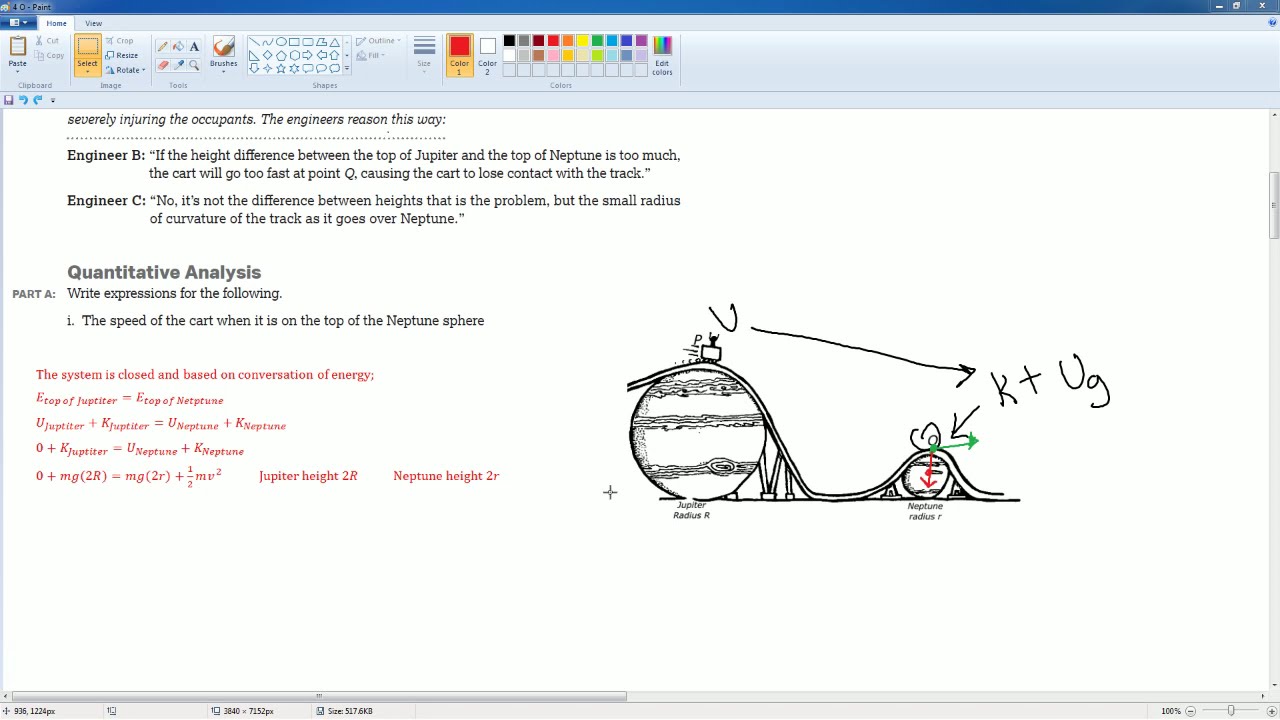
AP Physics Workbook 4.O Conservation of Energy and Circular Motion
AP Physics Workbook 5.I Momentum Representations
5.0 / 5 (0 votes)
Thanks for rating: