Loop-the-loop physics problem: Forces on a vertical loop.
TLDRThis video tackles the classic physics problem of determining the minimum hill height required for a block to smoothly navigate a loop without losing contact. The presenter explores limiting cases and applies Newton's Laws, circular motion principles, and conservation of energy to derive a solution. The key insight is identifying the speed at the top of the loop where the normal force becomes zero, leading to a formula that relates the hill height to the loop's radius. The final solution elegantly demonstrates that the minimum hill height is 2.5 times the radius of the loop, independent of the block's mass, highlighting the importance of geometry in this physical scenario.
Takeaways
- 📚 The video aims to solve a classic physics problem involving a block sliding down a hill and around a loop without losing contact.
- 🤔 The problem has perplexed physics students for decades and involves concepts from Newton's Laws, circular motion, and conservation of energy.
- 📉 Two limiting cases are discussed: a very high hill with a tiny loop where the block has enough speed to complete the loop, and a tiny hill with a large loop where the block does not make it all the way around.
- 🔍 A third case with a hill height equal to twice the radius of the loop is explored, where the outcome is uncertain and requires further analysis.
- 🔄 The conservation of energy principle is used to compare the energy at the top of the hill to the energy at the top of the loop.
- 🚀 The block's speed at the top of the loop is crucial for determining if it can complete the loop without losing contact with the track.
- 📐 Newton's Second Law is applied to find the relationship between the normal force, the object's weight, and the centripetal acceleration.
- ⚖️ The normal force equation is derived, showing it as the difference between the centripetal force and the gravitational force.
- 🎯 The critical speed at which the contact force becomes zero is found by setting the normal force to zero, resulting in a speed of √(g*R).
- 🔄 Substituting the critical speed back into the conservation of energy equation allows for the calculation of the minimum hill height required.
- 🏔️ The solution reveals that the minimum height of the hill must be 5/2 times the radius of the loop to ensure the block remains in contact throughout the loop.
Q & A
What is the main objective of the physics problem discussed in the video?
-The main objective is to find the minimum height of a hill required for a block to slide down, smoothly go around a loop, and always remain in contact with the loop.
Why has this problem been challenging for physics students?
-The problem is challenging because it involves a combination of Newton's Laws, circular motion, and the conservation of energy, which requires a deep understanding of these concepts to solve.
What are the three limiting cases sketched out on the board in the video?
-The three cases are: 1) A very high hill with a tiny loop, where the block carries a lot of speed and can go upside down around the loop. 2) A tiny hill with a very large loop, where the block might only make it halfway up the track before sliding back down. 3) A hill with a height equal to twice the radius or diameter of the loop, where it's uncertain whether the block will make it all the way around.
What is the significance of the normal force in the context of this problem?
-The normal force is the contact force between the track and the block. It's significant because it ensures that the block remains in contact with the loop during circular motion, and its calculation helps determine the minimum speed required for the block to complete the loop without losing contact.
How does the conservation of energy principle apply to the problem?
-The conservation of energy principle is applied by equating the gravitational potential energy at the top of the hill to the sum of the gravitational potential energy and kinetic energy at the top of the loop.
What is the minimum speed required for the block to make it to the top of the loop without losing contact?
-The minimum speed required is when the contact force becomes zero, which is achieved when the speed (V) is equal to the square root of gravitational acceleration (g) times the radius (R) of the loop, or V = sqrt(gR).
What happens when the block's speed is very high compared to gravity?
-When the block's speed is very high compared to gravity, the term v^2 / R becomes significantly larger than gravity, resulting in a large positive normal force and a strong contact force between the track and the block.
What is the final equation derived to determine the minimum height of the hill?
-The final equation derived is that the height of the hill (H) must be equal to 5 times the radius (R) divided by 2, or H = 5R / 2.
Why does the solution to the problem not depend on the mass of the object?
-The solution does not depend on the mass of the object because when the speed is substituted into the kinetic energy equation, the mass cancels out in all terms, making the height of the hill independent of the object's mass.
What is an example calculation based on the final equation if the radius of the loop is 4 meters?
-If the radius of the loop is 4 meters, the minimum height of the hill required would be 5 x 4 / 2 = 10 meters.
Outlines
🔍 Introduction to the Physics Loop Problem
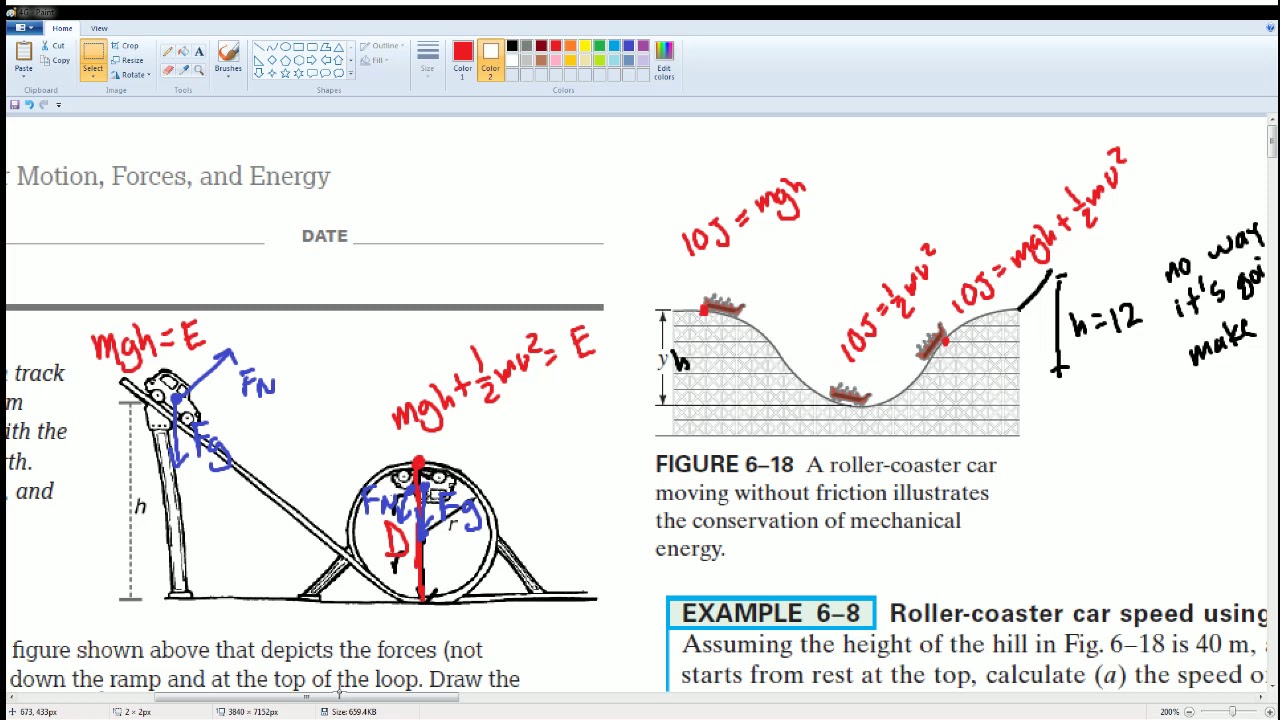
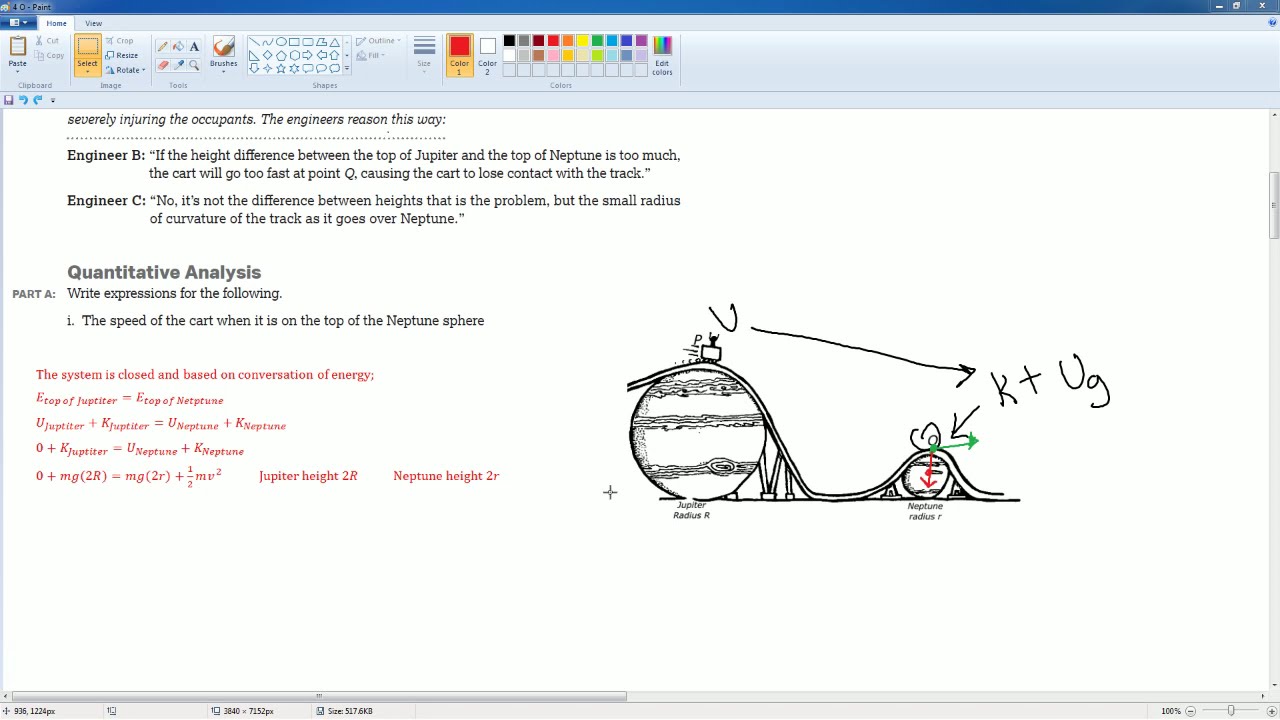
The video begins by introducing a classic physics problem: determining the minimum height required for a hill so that a block can slide down, go around a loop, and continue on the track without losing contact. This problem involves Newton's Laws, circular motion, and conservation of energy. The presenter outlines three limiting cases to conceptualize the problem: a very high hill with a tiny loop, a tiny hill with a large loop, and a hill height equal to twice the loop's radius or diameter. The goal is to find the critical speed at the top of the loop where the block just loses contact with the track.
📚 Analyzing Forces and Energy at the Top of the Loop
This paragraph delves into the forces acting on the block when it is at the top of the loop and upside down. The forces considered include the object's weight and the normal force from the track, which are both directed downward, and the centripetal force required for circular motion, which is also directed towards the center of the loop. The presenter sets up a coordinate system where downward forces are positive and upward forces are negative. By applying Newton's Second Law and the formula for centripetal acceleration, an equation for the normal force is derived. The critical speed at the top of the loop is then calculated, which is the speed at which the normal force becomes zero, ensuring the block just loses contact with the track.
🎯 Solving for the Minimum Hill Height Using Energy Conservation
The final paragraph focuses on solving for the minimum height of the hill using the principle of conservation of energy. The presenter revisits the energy at the top of the hill and at the top of the loop, equating gravitational potential energy with kinetic energy plus potential energy at the top of the loop. By substituting the previously found critical speed into the kinetic energy term, the presenter simplifies the equation to find the relationship between the hill's height and the loop's radius. The conclusion is that the hill's height must be 5/2 times the radius of the loop to ensure the block can safely navigate the loop without losing contact. The solution is independent of the block's mass, relying solely on the geometrical properties of the hill and the loop.
Mindmap
Keywords
💡Physics Loop Problem
💡Newton's Laws
💡Circular Motion
💡Conservation of Energy
💡Gravitational Potential Energy
💡Kinetic Energy
💡Normal Force
💡Centripetal Acceleration
💡Critical Speed
💡Limiting Cases
Highlights
The physics loop problem involves Newton's Laws, circular motion, and conservation of energy.
Three limiting cases are discussed: high hill with a tiny loop, tiny hill with a large loop, and a hill height equal to twice the loop's radius.
In the first case, a high hill allows the block to carry enough speed to complete the loop.
In the second case, a tiny hill with a large loop results in the block sliding back down after halfway up the track.
In the third case, the hill height is equal to twice the loop's radius, and the outcome is uncertain.
The normal force and weight are considered when analyzing the block at the top of the loop.
The block's speed at the top of the loop is crucial to determine if it can complete the loop without losing contact.
The conservation of energy equation is used to equate energy at the top of the hill to energy at the top of the loop.
The speed at the top of the loop is derived from the condition where the contact force equals zero.
The critical speed for the block to just make it around the loop is calculated as √(g * R).
Substituting the critical speed into the conservation of energy equation allows solving for the hill's height.
The minimum height of the hill is found to be 5/2 times the radius of the loop.
The solution is independent of the block's mass, ensuring a consistent answer regardless of the object's weight.
The final solution depends only on the geometry of the hill and the loop's radius.
An example calculation is provided for a loop with a 4m radius, requiring a minimum hill height of 10m.
The problem-solving approach highlights the importance of understanding the physics behind the loop and the block's motion.
Transcripts
Browse More Related Video

AP Physics Workbook 3.E Maximum speed over the top
AP Physics Workbook 4.G Circular Motion Forces and Energy

Conservation of Energy
AP Physics Workbook 4.O Conservation of Energy and Circular Motion
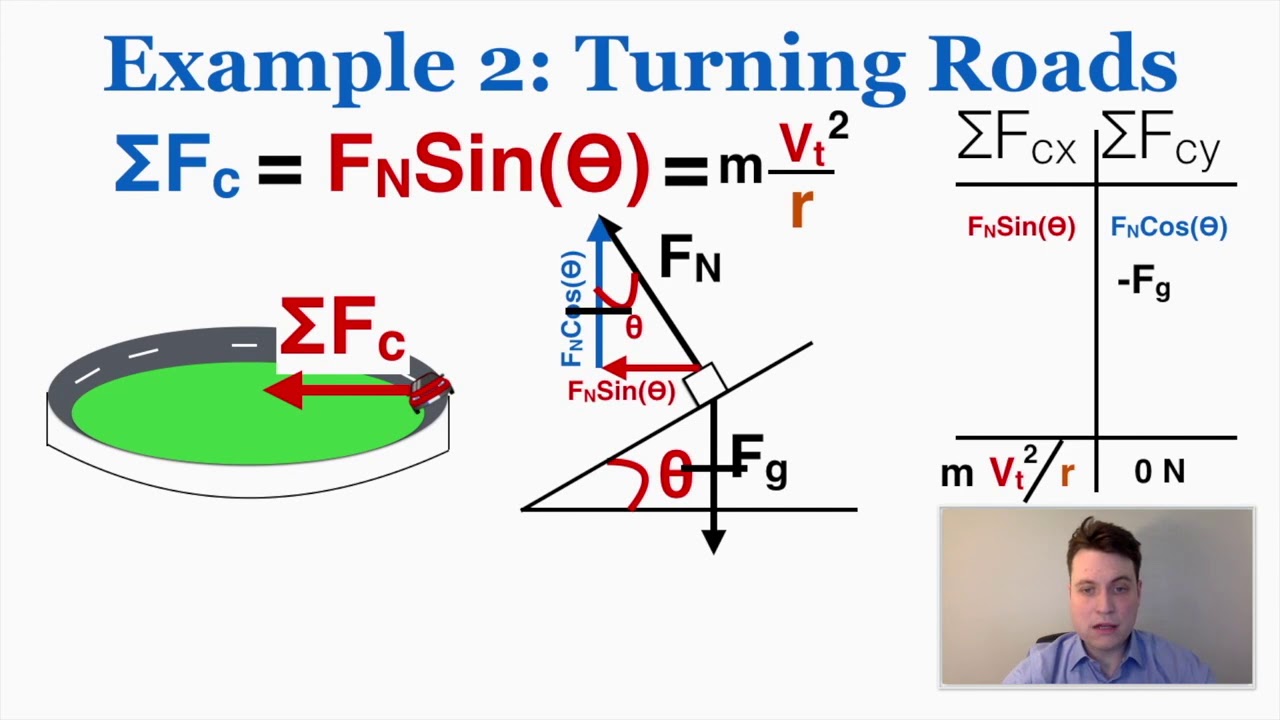
5 Examples of Solving Centripetal Force Problems - IB Physics

Calculate Normal Force On a Roller Coaster Cart | Circular Motion
5.0 / 5 (0 votes)
Thanks for rating: