2023 AP Calculus BC Free Response Question 5
TLDRThe video discusses solving questions from the 2023 AP Calculus BC Exam. It covers finding the area between two functions using integration, evaluating an improper integral, and solving an integral using integration by parts. The presenter explains the steps in detail, including vertical slicing, approximating areas, applying the fundamental theorem of calculus, and using logarithm properties. For the improper integral, they address the antiderivative process and the limit at infinity. Finally, they handle a new function involving the product of x and the derivative of another function, showcasing integration techniques and providing the final answers.
Takeaways
- 📚 The script discusses a problem from the 2023 AP Calculus BC Exam, specifically focusing on a question involving two functions, f and g, their graphs, and integrals.
- 📈 The problem involves finding the area enclosed by the graphs of f and g, which is approached by approximating the area of vertical slices and then integrating these approximations over the interval [0, 3].
- 🔍 The script mentions that while the equation for f(x) is not given, it is known to be twice differentiable, and the integral of f(x) from 0 to 3 is known to be 10.
- 📝 The integral of G(x) is calculated using a u-substitution method, and the integral from 0 to 3 is then subtracted from the integral of f(x) to find the area of the shaded region.
- 🧩 The script explains the use of the Fundamental Theorem of Calculus to evaluate the definite integrals, emphasizing the importance of correctly applying the limits of integration.
- 🔢 Part B of the problem asks for the evaluation of an improper integral, which is approached by considering the limit as the upper bound of integration approaches infinity.
- 🌐 The improper integral is found to converge to a finite value, which is calculated by evaluating the antiderivative at the limits of integration and taking the difference.
- 📉 The script provides a step-by-step walkthrough of the integration process, including the use of properties of logarithms and negative exponents to simplify expressions.
- 🆕 A new function H(x) is defined in the problem, which is the product of x and the derivative of f(x), and the script explains how to integrate this function using integration by parts.
- 🔄 Integration by parts is applied to H(x) by identifying u and dv, and then finding du and v, which leads to the evaluation of the integral from 0 to 3.
- 📊 The final answer for the integral of H(x) is found by evaluating the function at the limits of integration, subtracting the integral of f(x) from 0 to 3, and recognizing that f(3) is given as 2 in the problem statement.
- 🎯 The script concludes with the final answer for the integral of H(x), which is negative four, and emphasizes the importance of understanding the problem and applying the correct calculus techniques.
Q & A
What is the main topic discussed in the script?
-The script discusses a problem from the 2023 AP Calculus BC Exam, specifically focusing on the analysis of functions f and g, the area enclosed by their graphs, and the evaluation of integrals related to these functions.
What are the functions f and g in the context of the problem?
-The functions f and g are given in the problem, with the graph of g provided and the integral of f from 0 to 3 known. The specific equation for f is not given, but it is stated that f is twice differentiable.
What is the value of the integral of f(x) from 0 to 3?
-The value of the integral of f(x) from 0 to 3 is given as 10.
How is the area of the shaded region enclosed by the graphs of f and g determined?
-The area is determined by integrating the difference between the functions f(x) and g(x) from 0 to 3, which represents the sum of the areas of infinitely many vertical slices of the region.
What is the expression for the integral of G(x) from 0 to 3?
-The integral of G(x) from 0 to 3 involves a u-substitution where u is the denominator of G(x). The integral simplifies to 12 times the natural log of the absolute value of u, which after back substitution and evaluation, gives the area under the curve of G(x).
What is the purpose of the improper integral from 0 to infinity of G(x) squared?
-The purpose is to evaluate the value of this improper integral or to show that it diverges. This involves squaring G(x) and integrating the result, which requires careful handling of the infinite limit of integration.
How is the improper integral from 0 to infinity of G(x) squared evaluated?
-The improper integral is evaluated by replacing the infinite limit with a variable (e.g., r), squaring G(x), and then integrating. The limit as r approaches infinity is then taken to determine the convergence or divergence of the integral.
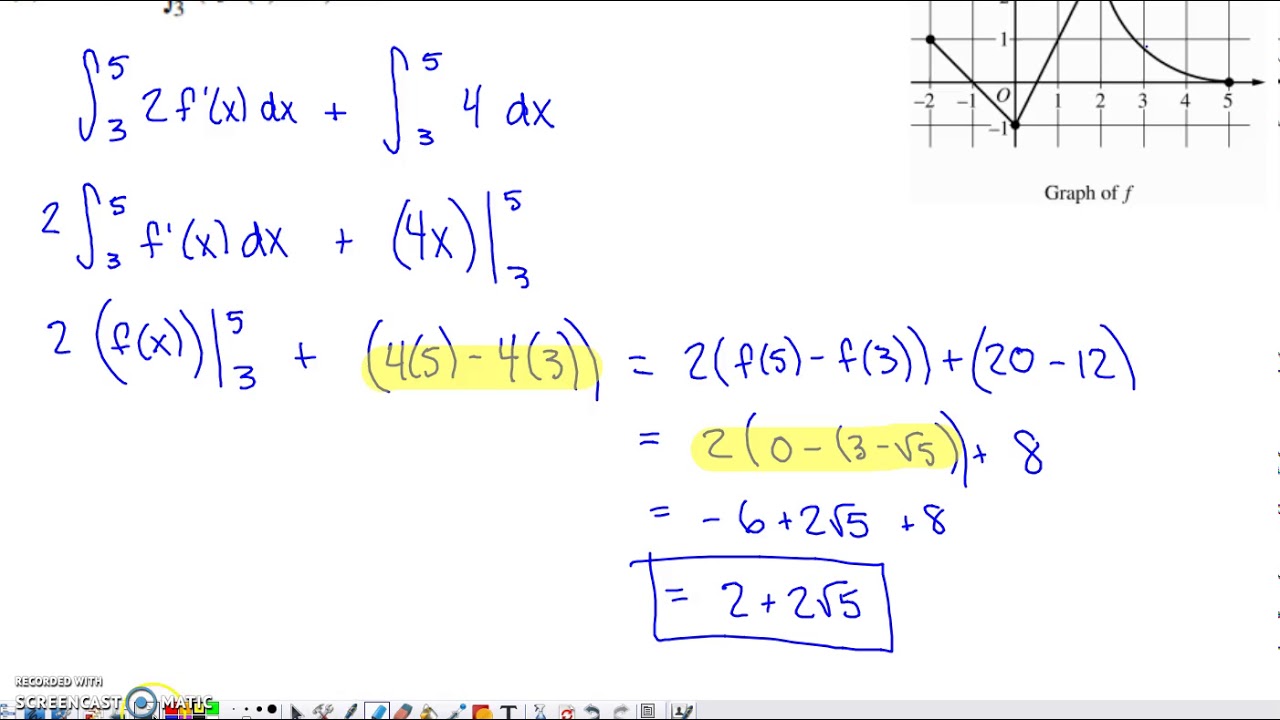
What is the new function H defined in the script?
-The function H is defined as the product of x and the derivative of F(x), denoted as H(x) = x * F'(x).
How is the integral of H(x) from 0 to 3 evaluated?
-The integral of H(x) from 0 to 3 is evaluated using integration by parts, where u is chosen as the first part of the product (x) and dv is the second part (F'(x)). The integral is then simplified and evaluated at the limits 0 and 3.
What is the final value of the integral of H(x) from 0 to 3?
-The final value of the integral of H(x) from 0 to 3 is found to be -4, after evaluating the integral at the limits and using the given information about the function F(x).
Outlines
📚 Calculus Exam Problem: Area Under Curves
The video script discusses a problem from the 2023 AP Calculus BC Exam, focusing on finding the area between the graphs of two functions, f and g, over the interval from 0 to 3. The script explains that while the equation for f(x) is not given, the graph and integral of f(x) from 0 to 3 are provided, with the integral equaling 10. The expression for G(x) is given, and F(x) is known to be twice differentiable. The solution involves breaking down the problem into three steps: slicing, approximating, and integrating. The area is approximated by taking vertical slices and using the difference between f(x) and G(x) as the height, multiplied by the width (Δx). The integral is then used to sum these areas, leading to the calculation of the area between the curves. The script also covers the use of u-substitution in integration and the application of the fundamental theorem of calculus. The final answer for the area is derived by subtracting the integral of G(x) from the integral of f(x), with the integral of f(x) known and the integral of G(x) calculated using u-substitution.
🔍 Evaluating Improper Integrals and New Function H
The second paragraph delves into evaluating an improper integral from 0 to infinity of G(x) squared. The script explains the process of squaring G(x) and carefully handling the notation to avoid errors. The integral is transformed by introducing a holding variable, r, to replace the infinite limit of integration. The script emphasizes the importance of recognizing that the antiderivative of a function raised to a negative power involves a division by the power minus one. The limit as r approaches infinity is calculated, showing that the integral converges to a finite value of 48. This indicates that the integral does not diverge. The paragraph also introduces a new function H, defined as the product of x and F'(x), and asks for the integral of H from 0 to 3. The solution involves integration by parts, where U is chosen as the first part of the product and DV as the second. The integral is then evaluated by substituting the values at the limits and subtracting the integral of f(x) from 0 to 3, which is given as 10. The final answer for the integral of H is -4, derived from evaluating the function at the limits and applying the given values for F(3) and the integral of f(x).
Mindmap
Keywords
💡AP Calc BC Exam
💡Functions f and g
💡Twice Differentiable
💡Integral
💡Shaded Region
💡Approximate Area
💡U-Substitution
💡Natural Logarithm
💡Improper Integral
💡Integration by Parts
💡Convergence
💡Fundamental Theorem of Calculus
Highlights
The discussion revolves around question five from the 2023 AP Calculus BC Exam.
Two functions, f and g, are given with their graphs and an expression for g(x).
Function f is twice differentiable, but its explicit equation is not provided.
The value of F(3) is given as 2.
The integral of f(x) from 0 to 3 is known to be 10.
Part A requires finding the area of the shaded region between the graphs of f and g.
The area calculation involves breaking down the region into slices and using integration.
The integral is set up from 0 to 3 to find the area between the functions.
The integral of f(x) from 0 to 3 is separated into two parts for calculation.
A u-substitution is used for the integral of G(x), with simplifications applied.
The fundamental theorem of calculus is applied to evaluate the integral.
Part B involves evaluating an improper integral of G(x) squared from 0 to infinity.
The improper integral is handled by replacing the infinity limit with a variable.
The convergence of the improper integral is determined by evaluating the limit as it approaches infinity.
A new function H is defined as the product of x and F'(x).
Integration by parts is used to find the integral of H(x) from 0 to 3.
The final answer for the integral of H(x) is negative four, derived from given values and calculations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: