AP physics Workbook 3.C Centrigual Force Part 2
TLDRThis video script discusses the physics of circular motion, focusing on the relationship between centripetal force and friction. It explains how a car turns when the centripetal force exceeds the frictional force and provides a detailed calculation to determine if a car will skid or follow a curve. The concept of static versus rotational friction is also explored, emphasizing the importance of ABS systems in vehicles to prevent wheel lock and maintain control during hard braking.
Takeaways
- 📚 The discussion revolves around circular motion and gravitational force, specifically focusing on unit three section three of an AP Physics workbook.
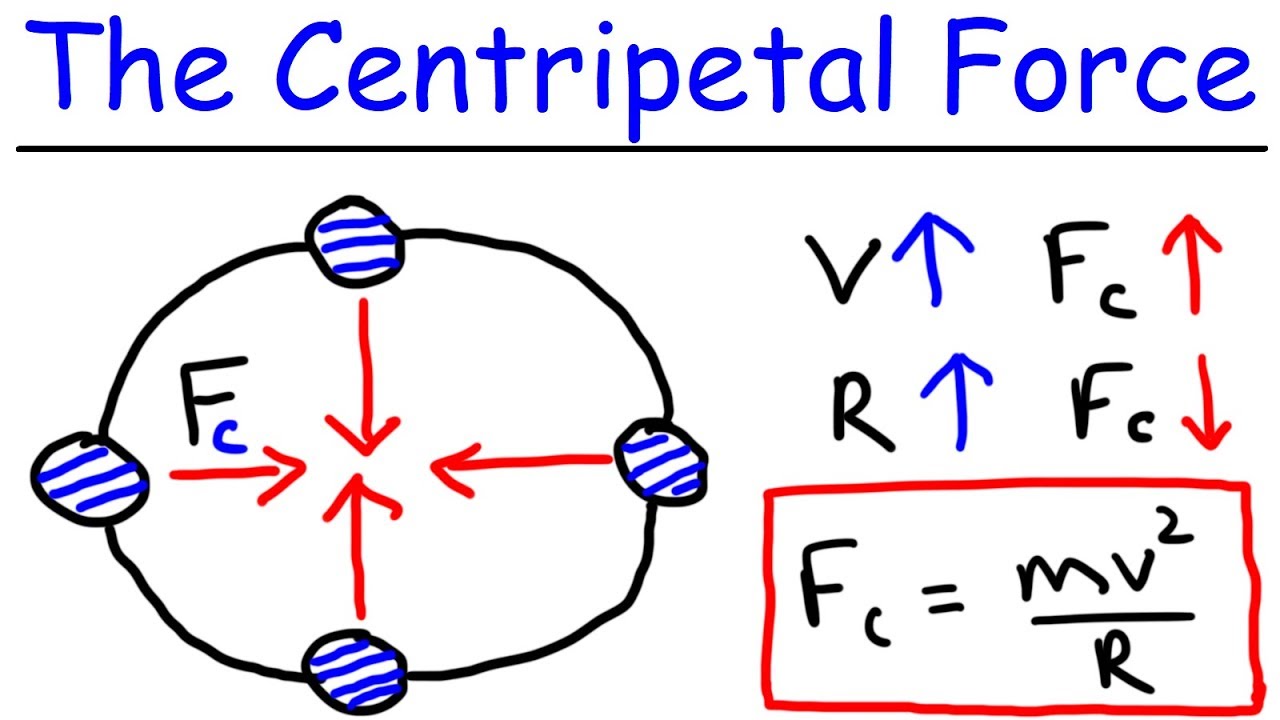
- 🔢 The critical condition for an object in circular motion is when the centripetal force (MV^2/R) exceeds the frictional force (MU_sF_n), leading to a potential change in motion.
- 🚗 In the context of a car turning, the frictional force is essential to provide the necessary centripetal force to keep the car moving along the curve.
- 📉 If the frictional force is insufficient (MV^2/R > MU_sF_n), the car will skid or slide off the intended path due to the inability to maintain the circular motion.
- 🔄 Centripetal acceleration is a key concept, defined by the formula MV^2/R, where M is mass, V is velocity, and R is the radius of the curve.
- 🚦 The example provided involves a car of mass 1000 kg taking a turn with a radius of 50 meters at a speed of 54 m/s, highlighting the importance of frictional force in maintaining the turn.
- 🌧️ Different road conditions, such as dry pavement (MU_s) and ice (MU_s lower), affect the car's ability to follow the curve due to variations in the frictional force.
- 💹 The relationship between turn radius (R) and velocity (V) is inversely proportional; as one increases, the other must decrease to maintain the required centripetal force.
- 🚨 A tighter turn (smaller R) requires the car to slow down more to safely navigate, as the centripetal force (F_R) felt by the car and passengers is greater.
- 🔒 The concept of static friction versus rotational friction is discussed, emphasizing the benefits of an anti-lock braking system (ABS) in vehicles to maintain static friction and prevent wheel lockup.
- 📈 The script concludes with a note on the importance of understanding the principles of circular motion and friction to apply in real-world scenarios, such as vehicle dynamics.
Q & A
What is the significance of the value MV^2/R being greater than the value of mu_s over Fn in the context of circular motion?
-When the centripetal force (MV^2/R) exceeds the frictional force (mu_s * Fn), it indicates that the friction between the tires and the road surface is not sufficient to keep the car moving in the desired circular path. As a result, the car will slide off the intended trajectory.
What is the role of static friction in maintaining circular motion?
-Static friction acts as the centripetal force that keeps an object, such as a car, moving in a circular path. It provides the necessary inward force to counteract the object's natural tendency to move in a straight line due to its momentum.
How does the coefficient of friction (mu_s) relate to the force of friction?
-The coefficient of friction (mu_s) is a dimensionless value that represents the frictional force between two surfaces. It is used to calculate the force of friction (F_friction) using the formula F_friction = mu_s * Fn, where Fn is the normal force.
What happens when a car turns on a curve with dry pavement versus ice?
-On dry pavement, the coefficient of friction is higher, allowing for sufficient static friction to maintain the turn. However, on ice, the coefficient of friction is lower, reducing the frictional force, which may not be enough to prevent the car from skidding.
How does the radius of a turn (R) affect the required velocity (V) for a car to safely navigate the turn?
-As the radius of a turn increases, the required centripetal force decreases, which means the car can maintain a higher velocity without skidding. Conversely, for a smaller radius turn, the car must reduce its velocity to ensure the frictional force is sufficient to provide the necessary centripetal force.
What is the difference between static friction and kinetic friction?
-Static friction is the force that prevents an object from starting to move across a surface until a certain threshold is reached. Kinetic friction, also known as sliding friction, is the force that opposes the relative motion between two surfaces in contact when they are already moving. The coefficient of static friction (mu_s) is typically greater than the coefficient of kinetic friction (mu_k), making static friction more effective at preventing skidding.
Why are anti-lock braking systems (ABS) important in vehicles?
-ABS prevents the wheels from locking up during hard braking, which can cause skidding. By allowing the wheels to continue rotating, the vehicle maintains a higher coefficient of static friction compared to the kinetic friction experienced during a skid, providing better control and reducing the risk of accidents.
How does the centripetal acceleration formula (a = V^2/R) relate to the forces acting on a car during a turn?
-The centripetal acceleration formula calculates the acceleration required to keep an object moving in a circular path. In the case of a car turning, this formula helps determine the necessary centripetal force (which is provided by friction) to keep the car moving along the curve without skidding off.
What is the effect of increasing the radius of a turn on the car's velocity?
-If the radius of a turn is increased, the car can maintain a higher velocity without the risk of skidding, as the required centripetal force is lower. This is because the force needed to keep the car in circular motion is directly proportional to the square of the velocity and inversely proportional to the radius.
How does the velocity of a car affect the frictional force experienced during a turn?
-As the velocity of a car increases, the centripetal force required to keep it in a circular path also increases (since F_c = m * V^2 / R). If the frictional force is not sufficient to provide this increased force, the car may skid or slide off the intended path.
What is the importance of understanding the relationship between centripetal force, friction, and velocity in vehicle dynamics?
-Understanding these relationships is crucial for vehicle safety and performance. It helps in designing roads, vehicle suspension systems, and safety features like ABS. It also aids in predicting vehicle behavior in different driving conditions and understanding how to safely navigate turns at various speeds.
Outlines
📚 Physics Concepts: Centripetal Force and Friction
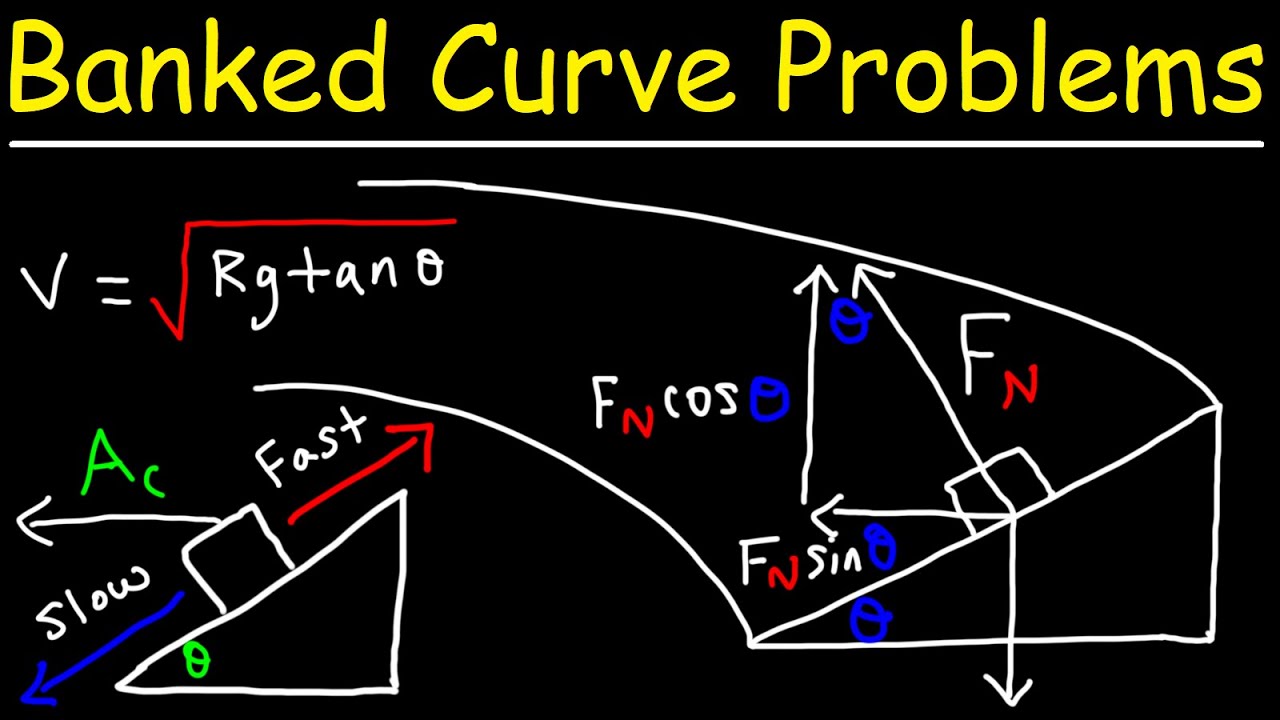
The paragraph discusses the physics concepts of centripetal force and friction in the context of a car moving in a circular motion. It explains the scenario where the centripetal force (MV^2/R) is greater than the friction force (Mu_sF_n), leading to the car sliding off the curve. The explanation includes the role of static friction in maintaining circular motion and how the force exerted by the tires on the road provides the necessary centripetal force. The paragraph also touches on the calculation of these forces and how the magnitude of friction affects the car's ability to follow the curve.
📈 Calculation of Centripetal Force and Friction
This paragraph delves into the calculation of centripetal force and friction for a car rounding a curve. It provides an example of a car with a given mass and velocity, and how to determine whether the car will follow the curve or skid, based on the coefficient of friction of the pavement (dry or icy). The paragraph explains the formula for centripetal acceleration and force, and how to calculate the normal force. It also compares the friction force on dry pavement and ice, highlighting the difference in the car's behavior due to varying friction coefficients.
🚗 Turning Dynamics: Left vs Right Turn
The focus of this paragraph is on the dynamics of turning left versus right and the impact on the truck's speed for safe turning. It discusses the relationship between the radius of the turn (R) and the required centripetal force (F_R), explaining how a larger radius (right turn) results in less force being exerted on the truck. The paragraph also explores the effect of doubling the radius on the force and velocity, concluding that a smaller radius (tighter turn) requires the truck to slow down more to balance the equation of MV^2/R.
🔄 Static vs Rotational Friction in Car Turning
This paragraph discusses the concepts of static and rotational friction in the context of a car turning. It explains the role of an anti-lock braking system (ABS) in preventing wheels from locking and skidding, which is worse than wheel lock in terms of friction. The paragraph emphasizes the importance of static friction for better braking and control during turns, as it has a higher coefficient than kinetic friction. It concludes by reinforcing the understanding of why modern cars are equipped with ABS systems to maintain the advantages of static friction during hard braking.
Mindmap
Keywords
💡Circular Motion
💡Centripetal Force
💡Friction Force
💡Coefficient of Friction
💡Acceleration
💡Momentum
💡Inertia
💡Static Friction
💡Anti-lock Braking System (ABS)
💡Kinetic Friction
💡Centripetal Acceleration
Highlights
Explaining the physical concept when the value of MV squared R is greater than the value of MU s over F n, which relates to circular motion and gravitational forces.
Describing the friction force as a key element in maintaining circular motion, and its mathematical representation as mu s times the normal force.
Discussing the scenario where the force of friction is not sufficient to keep a car moving in a circular path, leading to the car sliding off the turn.
Providing a clear example of a car turning and the role of centripetal force, acceleration, and velocity in this motion.
Explaining the relationship between the force of friction and the centripetal force required for a car to move in a curve on a flat road.
Calculating the force normal and comparing it to the force needed to produce centripetal acceleration to determine if a car will follow a curve or skid.
Using a specific example of a 1000 kg car rounding a curve with a radius of 50 meters at a speed of 54 meters per second to illustrate the principles discussed.
Discussing the impact of the coefficient of friction on the force of friction and how it affects a car's ability to turn on different surfaces like dry pavement and ice.
Exploring the concept of static friction versus rotational friction, and how they relate to a car's tires in motion and during braking.
Highlighting the benefits of an anti-lock braking system (ABS) in cars, which prevents wheels from locking and allows for better use of static friction during hard braking.
Comparing the coefficients of static friction (mu s) and kinetic friction (mu K), and noting that static friction is always greater than kinetic friction.
Discussing how the radius of a turn affects the required velocity for safe turning, and how a smaller radius requires the truck to slow down more.
Explaining the mathematical relationship between velocity, radius, and centripetal force, and how changes in one variable affect the others.
Providing a comprehensive understanding of the physical principles at play during a car's turn, and the importance of balancing these forces for safe driving.
Summarizing the key points and calculations from the transcript, offering a clear and concise review of the concepts discussed.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: