Confidence Interval for a population mean - t distribution

Joshua Emmanuel
9 Mar 202207:40
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explains the process of constructing confidence intervals for a population mean using the Student t-distribution. It emphasizes the importance of the sample size and the concept of degrees of freedom in determining the t-critical value. The video illustrates how the margin of error is calculated and how it affects the width of the confidence interval. Through examples, it demonstrates the estimation of population mean with different confidence levels and sample sizes, highlighting the central limit theorem's role in larger samples and the impact of sample size on the precision of the confidence interval.

Takeaways
  • ๐Ÿ“Š A confidence interval is a range of values estimated to include the population parameter at a given confidence level.
  • ๐Ÿงฎ When the population standard deviation is unknown, the sample standard deviation and t-distribution are used instead of the Z distribution.
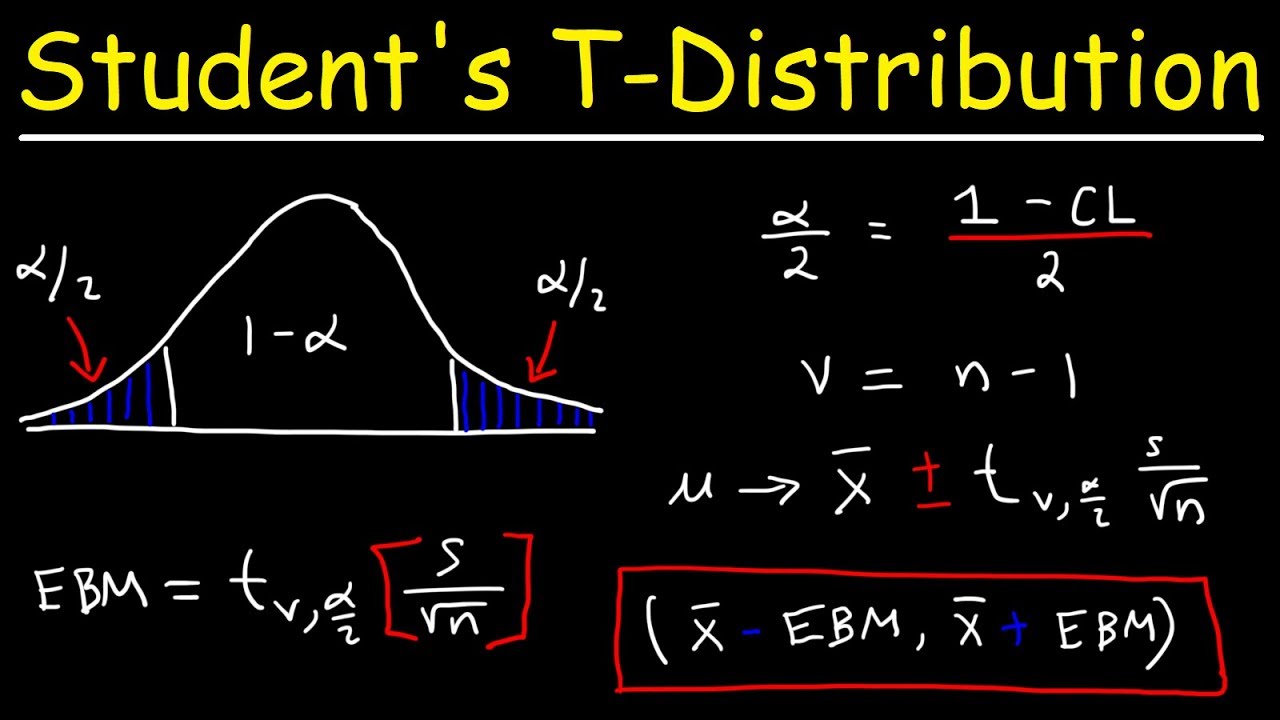
  • ๐Ÿ”„ The t-distribution is similar to the normal distribution but has a larger standard deviation, making it flatter.
  • ๐Ÿ”ข The shape of the t-distribution is determined by the degrees of freedom, which is calculated as the sample size minus one (n - 1).
  • ๐Ÿ“‰ As degrees of freedom increase, the t-distribution more closely resembles the Z distribution.
  • ๐Ÿ” The t-critical value is found using a table or software, based on the desired confidence level and degrees of freedom.
  • ๐Ÿ“ˆ The margin of error for estimating the population mean is calculated using the sample standard deviation, sample size, and t-critical value.
  • ๐Ÿ”– For small sample sizes, the assumption of normal population distribution is necessary, but this assumption becomes unnecessary for larger sample sizes due to the central limit theorem.
  • ๐Ÿ“‰ Increasing the sample size decreases the margin of error, resulting in a narrower confidence interval, while a higher confidence level increases the critical value and margin of error, leading to a wider interval.
  • ๐ŸŒŸ The confidence interval is an estimate and may or may not contain the true population mean, but it provides a range within which the population mean is expected to fall with a certain level of confidence.
Q & A

  • What is a confidence interval for a population mean?

    -A confidence interval for a population mean is a range of values, derived from sample data, that is likely to include the population parameter at a specified confidence level.

  • How is the margin of error calculated in constructing a confidence interval?

    -The margin of error is calculated by taking the sample standard deviation, multiplying it by the t-critical value and dividing by the square root of the sample size (n).

  • Why is the t-distribution used instead of the Z distribution when constructing a confidence interval?

    -The t-distribution is used when the population standard deviation is unknown and is replaced with the sample standard deviation. It is more appropriate for smaller sample sizes, whereas the Z distribution is used when the population standard deviation is known.

  • What are the key differences between the t-distribution and the standard normal (Z) distribution?

    -Both t-distribution and Z distribution are bell-shaped with a mean of 0 and an area of 1 under the curve. However, the t-distribution has a greater standard deviation than the Z distribution, making it flatter. Additionally, there is a family of t-distributions, each with a shape determined by the degrees of freedom (df), whereas there is only one standard normal distribution.

  • How does the degrees of freedom (df) affect the shape of the t-distribution?

    -The shape of the t-distribution is determined by the degrees of freedom, which is based on the sample size (n). As the degrees of freedom increase, the t-distribution becomes more similar to the standard normal (Z) distribution.

  • What is the significance of the sample size in determining whether to use the central limit theorem?

    -Sample sizes of at least 30 are generally considered large enough for the central limit theorem to apply, allowing the use of the Z distribution without assuming a normal population distribution. Smaller sample sizes require the assumption of normality or the use of the t-distribution.

  • How does the confidence level affect the margin of error in a confidence interval?

    -A higher confidence level results in a larger critical value, which in turn increases the margin of error, resulting in a wider confidence interval. Conversely, a lower confidence level will produce a smaller margin of error and a narrower confidence interval.

  • What is the formula for calculating the margin of error when constructing a confidence interval for a population mean?

    -The margin of error is calculated using the formula: margin of error = t_ฮฑโ„2 * (s / โˆšn), where t_ฮฑโ„2 is the critical t-value, s is the sample standard deviation, and n is the sample size.

  • How does the sample size affect the width of the confidence interval?

    -Increasing the sample size will decrease the margin of error, resulting in a narrower confidence interval. Conversely, reducing the sample size will increase the margin of error, leading to a wider confidence interval.

  • What happens when the sample size is large enough to apply the central limit theorem?

    -When the sample size is large (at least 30), the central limit theorem states that the distribution of sample means will be approximately normal, regardless of the population distribution. This eliminates the need to assume a normal population distribution for the calculations.

  • How can one find the critical t-value for a given confidence level and degrees of freedom?

    -The critical t-value for a given confidence level and degrees of freedom can be found using a t-distribution table or statistical software. The t-value corresponds to the right tail area or two tails alpha, depending on the confidence level specified.

Outlines
00:00
๐Ÿ“Š Introduction to Confidence Intervals and t-Distribution

This paragraph introduces the concept of constructing confidence intervals for a population mean using the Student t distribution. It explains that a confidence interval is a range of values that is likely to contain the population parameter at a specified confidence level. The paragraph outlines the process of determining the margin of error by using the sample mean and the t-distribution, which is necessary when the population standard deviation is unknown. It also discusses the t-distribution's similarity to the standard normal distribution and its dependence on degrees of freedom (df), which is based on the sample size n. The paragraph further explains how to use the t-distribution table to find the critical values for constructing the confidence interval.

05:05
๐Ÿงฎ Calculation and Interpretation of Confidence Intervals

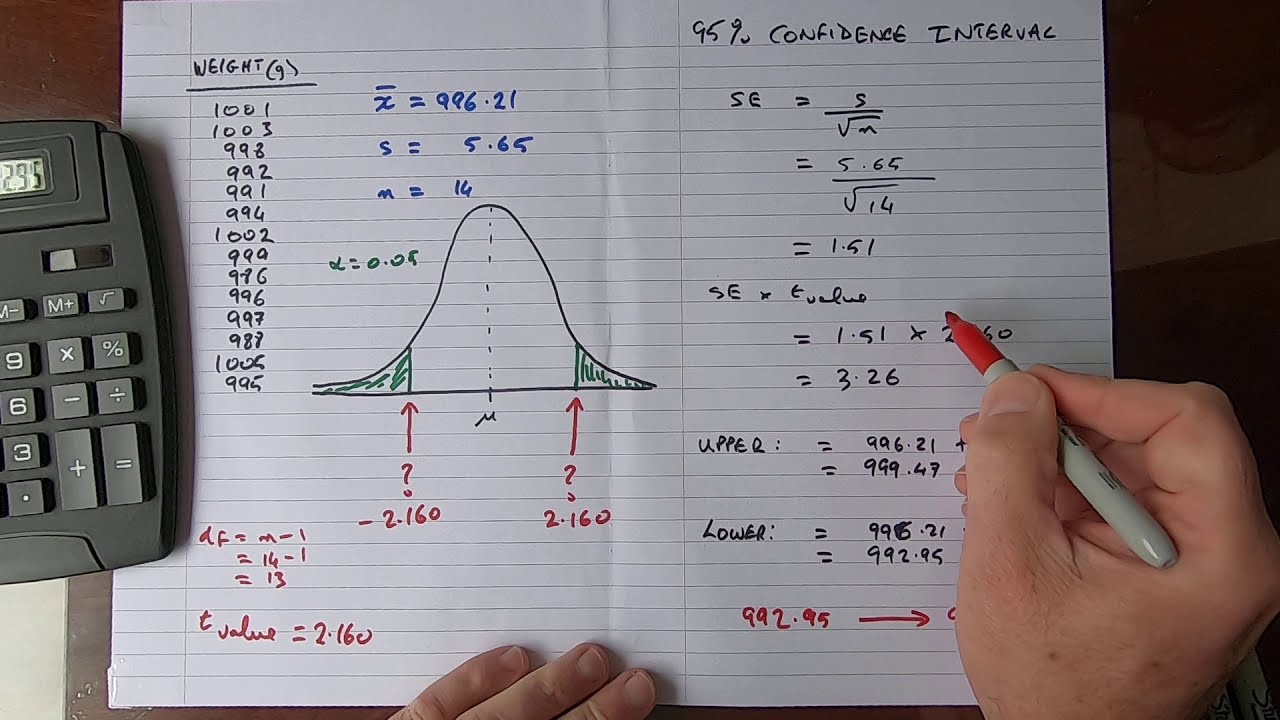
This paragraph delves into the specifics of calculating the margin of error and confidence intervals for a population mean, given the sample standard deviation. It details the formula for the margin of error, which includes the critical t-value, sample standard deviation, and sample size. The paragraph emphasizes the significance level and how it relates to the confidence level. It provides an example with a sample size of 15 and a standard deviation of 3.5 to illustrate the process of estimating the population mean with a 95% confidence level. The paragraph also touches on the central limit theorem and its implications for small and large sample sizes. It concludes with an interpretation of the confidence interval, stating that there is a 95% confidence that the true population mean falls within the calculated range.

๐Ÿ”ข Impact of Sample Size and Confidence Level on Confidence Intervals

This paragraph discusses the impact of sample size and confidence level on the width of the confidence interval. It explains how increasing the sample size decreases the margin of error, resulting in a narrower confidence interval, while a higher confidence level leads to a larger critical value and a wider interval. The paragraph provides a second example with a sample size of 85 and a 99% confidence level to demonstrate these concepts. It also addresses the practicality of using t-tables and software for finding critical values when the degrees of freedom are not directly listed. The paragraph concludes by reiterating the concept that the constructed confidence interval represents the range within which the population mean is expected to fall with a certain level of confidence.

Mindmap
Keywords
๐Ÿ’กconfidence interval
A confidence interval is a range of values, derived from sample data, that is likely to include the population parameter with a certain level of confidence. In the context of the video, it is used to estimate the population mean when the true value is unknown. The video explains that the confidence interval is constructed by adding and subtracting a margin of error from the sample mean. For instance, the video provides an example where a sample mean of 20 with a margin of error of 1.94 results in a 95% confidence interval of 18.06 to 21.94, indicating that we are 95% confident the true population mean falls within this range.
๐Ÿ’กpopulation mean
The population mean refers to the average value of a parameter for an entire population. In statistical terms, it is the central value of a dataset from which samples are drawn. The video's main theme revolves around estimating this unknown population mean using a confidence interval. It is illustrated that the population mean is what we are trying to infer from the sample data, such as when the video discusses estimating the population mean with a 95% confidence level.
๐Ÿ’กStudent t distribution
The Student t distribution, also known simply as the t distribution, is a type of statistical distribution that is similar to the normal distribution but has heavier tails. It is used when the population standard deviation is unknown and is estimated by the sample standard deviation. The video explains that the t distribution is used to determine the margin of error in constructing the confidence interval for the population mean, especially when the sample size is small. As the degrees of freedom increase, the t distribution approaches the Z distribution, which is used for larger sample sizes.
๐Ÿ’กsample mean
The sample mean is the average of the data values in a sample, and it serves as the point estimate for the population mean. In the video, the sample mean is used as the starting point for constructing the confidence interval. It is emphasized that the sample mean, along with the margin of error, helps to estimate the range within which the population mean is likely to fall. For example, in the video's illustration, a sample mean of 20 is used to calculate the confidence interval for the population mean.
๐Ÿ’กmargin of error
The margin of error is the difference between the confidence interval limits and the sample mean. It measures the uncertainty associated with the estimate of the population parameter. In the context of the video, the margin of error is calculated by using the t-distribution and is added to and subtracted from the sample mean to form the confidence interval. The video provides an example where the margin of error is 1.94 for a 95% confidence interval, contributing to the interval's lower and upper limits.
๐Ÿ’กdegrees of freedom
Degrees of freedom (df) in the context of the t distribution refers to the number of independent values in the data set that are free to vary. It is calculated as n - 1, where n is the sample size. The video explains that the shape of the t distribution is determined by the degrees of freedom, with more degrees of freedom resulting in a distribution that more closely resembles the standard normal distribution. The video also illustrates that for a sample size of 15, the degrees of freedom is 14, which is used to find the t-critical value for constructing the confidence interval.
๐Ÿ’กt-critical value
The t-critical value is the value from the t distribution that corresponds to a specific confidence level and degrees of freedom. It is used to calculate the margin of error in the confidence interval for the population mean. The video describes how to find the t-critical value using a t-distribution table or software, and it provides an example where for 95% confidence and 14 degrees of freedom, the t-critical value is 2.145.
๐Ÿ’กsample size
Sample size refers to the number of observations or individuals in a sample. In the video, it is emphasized that the sample size affects the precision of the confidence interval and the applicability of the central limit theorem. A larger sample size results in a smaller margin of error and a narrower confidence interval, as illustrated by the example with a sample size of 85 leading to a 99% confidence interval with a margin of error of 1.00.
๐Ÿ’กcentral limit theorem
The central limit theorem is a statistical theory that states that the distribution of sample means approaches a normal distribution as the sample size becomes large, regardless of the population distribution. The video explains that for sample sizes of at least 30, this theorem allows us to assume normality without needing to know the population distribution. This is contrasted with smaller sample sizes, where the assumption of normality is necessary for the t-distribution to be applicable.
๐Ÿ’กstandard deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. In the context of the video, the sample standard deviation is used in place of the population standard deviation when constructing the confidence interval for the population mean. The video mentions that the standard deviation, along with the sample size and the t-critical value, is a key component in calculating the margin of error for the confidence interval.
๐Ÿ’กconfidence level
The confidence level is the probability that the confidence interval contains the true population parameter. It is expressed as a percentage and is a critical aspect of constructing confidence intervals. The video explains that for a 90% confidence level, the significance level (alpha) is 0.10, which is divided into two tails. This means that there is a 90% chance that the true population mean falls within the calculated confidence interval. The video provides examples of constructing confidence intervals at both 95% and 99% confidence levels.
Highlights

The video discusses constructing confidence intervals for a population mean using the Student t distribution.

A confidence interval is a range of values likely to include the population parameter at a specified confidence level.

The margin of error is calculated by adding and subtracting it from the sample mean.

When the population standard deviation is unknown, the sample standard deviation and t-distribution are used.

The t-distribution is similar to the standard normal distribution but has a greater standard deviation, making it flatter.

The shape of the t-distribution is determined by degrees of freedom, which is based on the sample size n.

As degrees of freedom increase, the t distribution approaches the Z distribution.

The t-distribution table provides critical values for constructing confidence intervals.

The formula for the margin of error includes the t critical value, sample standard deviation, and sample size.

The significance level is 1 minus the confidence level, and it determines the critical values for the confidence interval.

For a small sample size of 12, the degrees of freedom is 11, and the critical value for a 90% confidence level is 1.796.

A sample size of 15 with a mean of 20 and standard deviation of 3.5 is used to estimate the population mean with a 95% confidence level.

For a sample size of 85, a 99% confidence interval is constructed, and the central limit theorem applies, assuming normal distribution.

Increasing the sample size decreases the margin of error, resulting in a narrower confidence interval.

A higher confidence level results in a larger critical value, a larger margin of error, and a wider confidence interval.

The video concludes by emphasizing the concept of confidence intervals and their use in estimating population parameters.

Transcripts

Browse More Related Video

Student's T Distribution - Confidence Intervals & Margin of Error

How To...Calculate the Confidence Interval for a Sample

Elementary Statistics - Chapter 7 - Estimating Parameters and Determining Sample Sizes Part 2

7.2.0 Estimating a Population Mean - Lesson Overview, Key Concepts, Learning Outcomes

Confidence Interval for a population proportion | Solved Problems

Math 14 HW 7.2.5-T Find critical t value, margin of error & confidence interval for population mean.

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistical AnalysisConfidence Intervalst-DistributionSample SizePopulation MeanDegrees of FreedomCentral Limit TheoremData AnalysisProbabilityStatistical Inference