Introduction to the line integral | Multivariable Calculus | Khan Academy
TLDRThe video script discusses the concept of calculating the area under a curve in two dimensions using definite integrals and extends this idea to find the surface area of a wall or fence following a curvy path in three dimensions. It introduces the analogy of infinitesimally small changes in x (dx) and y (dy) and their corresponding changes in arc length (ds), and how these can be related using the Pythagorean theorem. The script then outlines the process of expressing the integral in terms of a parameter t, by utilizing the derivatives of x and y with respect to t, ultimately leading to a definite integral that can be evaluated to find the area.
Takeaways
- 📐 The concept of finding the area under a curve in two dimensions using definite integrals is introduced.
- 🔄 The process involves breaking the area into infinitesimally small rectangles and summing their areas.
- 📈 The script extends the idea to three dimensions, considering a path in the x-y plane and a function f(x, y) that assigns a value to each point.
- 🌐 The challenge is to find the area of a 'curtain' or 'fence' that follows a curvy path in the x-y plane and reaches up to a surface defined by f(x, y).
- 📊 The analogy of changing the base of integration from a straight line to a curvy path helps visualize the problem.
- 🛤️ The concept of arc length (ds) is introduced to relate the infinitesimally small changes in x and y to the path's geometry.
- 📐 The Pythagorean Theorem is used to express ds in terms of dx and dy, which are related to the path's parameter t.
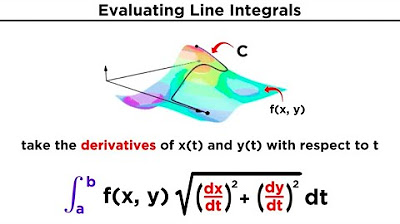
- 🔄 The area of the curvy wall is expressed as an integral from t=a to t=b of f(x(t), y(t)) times the square root of (dx/dt)^2 + (dy/dt)^2.
- 📈 The derivatives of x and y with respect to t, denoted as g'(t) and h'(t), are used to express the differential changes in x and y in terms of t.
- 🌟 The script emphasizes the importance of understanding the geometric interpretation and the algebraic manipulation of integrals and differentials to solve the problem.
- 🔍 The final formula for the area in terms of t will be explored in a subsequent video, demonstrating how to evaluate such a definite integral.
Q & A
What is the main concept discussed in the video?
-The main concept discussed in the video is finding the area under a curve in two dimensions and extending this concept to find the surface area of a wall or fence along a curvy path in three dimensions.
What is the basic idea behind finding the area under a curve?
-The basic idea behind finding the area under a curve is to divide the area into infinitely small rectangles, each with a height equal to the function's value at a specific point and a width that is an infinitesimally small change in x (dx), and then sum up the areas of all these rectangles.
What is the term used for the infinitely small changes in x and y?
-The term used for the infinitely small changes in x and y is differentials, represented as dx and dy, respectively.
How is the length of the path in the x-y plane represented?
-The length of the path in the x-y plane is represented by the differential ds, which is the infinitesimal change in arc length of the curve.
What is the relationship between ds, dx, and dy?
-The relationship between ds, dx, and dy is given by the Pythagorean Theorem, where ds is the hypotenuse of a right triangle with dx and dy as the other two sides. Mathematically, ds is equal to the square root of (dx squared + dy squared).
What is the purpose of converting the expression for the area into terms of the parameter t?
-The purpose of converting the expression for the area into terms of the parameter t is to simplify the calculation of the definite integral, as it allows us to express the square root of the sum of the derivatives squared (dx/dt and dy/dt) with respect to the parameter t.
What is the final form of the integral for the surface area along the curvy path?
-The final form of the integral for the surface area along the curvy path is the integral from t=a to t=b of the function f(x(t), y(t)) times the square root of ((dx/dt)^2 + (dy/dt)^2) dt, where x(t) and y(t) are the parametric equations of the path and f(x, y) is the function that assigns a value to each point in the x-y plane.
How does the video script relate the concept of definite integrals in two dimensions to three dimensions?
-The video script relates the concept of definite integrals in two dimensions to three dimensions by extending the idea of finding the area under a curve to finding the surface area along a curvy path in the x-y plane, which involves a third dimension represented by the function f(x, y).
What is the role of parameterization in solving this problem?
-Parameterization plays a crucial role in solving this problem as it allows us to define the curvy path in the x-y plane using two functions of a single parameter t, which in turn helps us express the derivatives dx/dt and dy/dt needed to calculate the surface area integral.
How does the video script help in visualizing the problem?
-The video script helps in visualizing the problem by providing a step-by-step analogy from the simpler concept of finding the area under a curve in two dimensions to the more complex concept of finding the surface area along a curvy path in three dimensions. It uses diagrams and examples to illustrate the concepts of differentials, arc length, and the final integral expression.
What is the significance of the function f(x, y) in this context?
-The function f(x, y) is significant in this context as it represents the height or value associated with each point in the x-y plane. The surface area of the fence or curtain along the curvy path is determined by the values of f(x, y) and the path's geometry, which is defined by the parametric equations x(t) and y(t).
Outlines
📐 Introduction to Finding Area Under a Curve
This paragraph introduces the concept of calculating the area under a curve in two dimensions using the definite integral as a tool. It explains the process of breaking the area into infinitesimally small rectangles and summing their areas. The discussion includes drawing a function f(x) on the x-y plane and finding the area between two points a and b on the x-axis. The paragraph sets the stage for extending this concept to more complex problems in higher dimensions.
📈 Expanding to 3D Space and Path Definition
The second paragraph transitions the discussion from 2D to 3D space, emphasizing the need to parameterize both x and y variables to define a path in the x-y plane. It introduces the concept of a surface associated with every point in the x-y plane using a function f(x, y) and visualizes it as a 3D plot. The paragraph aims to find the area of a 'curtain' or 'fence' that follows a curvy path in the x-y plane and reaches up to the surface defined by f(x, y). It also touches on the idea of visualizing the intersection of the 'curtain' with the surface to understand the shape of the area in question.
🔢 Calculating the Area Along a Curvy Path
This paragraph delves into the mathematical approach of calculating the area along a curvy path in the x-y plane. It introduces the concept of a small change in the arc length of the curve (ds) and relates it to the Pythagorean theorem by expressing ds as the square root of the sum of the squares of infinitesimal changes in x and y (dx and dy). The paragraph aims to transform the integral expression to involve only the parameter t, which is used to express x and y in the path definition. It concludes with the intention of making the mathematical process more concrete through a tangible problem in the subsequent video.
📚 Simplified Line Integral in Terms of Parameter t
The final paragraph focuses on simplifying the line integral to a more manageable form by expressing everything in terms of the parameter t. It explains how to algebraically manipulate differentials to rewrite the integral in a form that is ready for evaluation. The paragraph outlines the process of substituting dx/dt and dy/dt (the derivatives of x and y with respect to t) into the integral and highlights that this transformation turns the complex line integral into a simple definite integral that can be calculated in the next video. The summary emphasizes the transition from a visually complex 3D problem to a more straightforward 1D calculation.
Mindmap
Keywords
💡Two dimensions
💡Definite integral
💡dx
💡Three dimensions
💡Parametric equations
💡Surface
💡Curtain or fence analogy
💡Arc length
💡Differentials
💡Line integral
💡dt
Highlights
The concept of finding the area under a curve in two dimensions using definite integrals.
The introduction of infinitesimally small changes in x, denoted as dx, to calculate areas under curves.
The extension of two-dimensional area calculation to three dimensions and beyond.
The use of parameterized paths in the x-y plane to define curves mathematically.
The concept of associating each point in the x-y plane with a value using a function f(x, y).
The visualization of a surface in three dimensions defined by the function f(x, y).
The challenge of calculating the area of a 'curvy wall' or fence along a path in the x-y plane.
The analogy of a curtain or fence to visualize the area between a curve and a surface.
The mathematical concept of arc length and its relation to small changes in distance along a curve.
The use of the Pythagorean Theorem to relate changes in x and y to the arc length ds.
The transformation of the area calculation into a definite integral involving f(x, y) and the square root of dx^2 + dy^2.
The process of expressing the integral in terms of the parameter t by substituting x and y with functions of t.
The derivation of dx/dt and dy/dt, which are the key components for calculating the area along a curvy path.
The final integral formula that expresses the area calculation in terms of the parameter t, allowing for practical applications.
The promise of a concrete example in the next video to demonstrate the practical application of the derived formula.
The potential of this mathematical framework to simplify complex area calculations in multi-dimensional spaces.
Transcripts
Browse More Related Video
Evaluating Line Integrals

2011 Calculus BC free response #1d | AP Calculus BC | Khan Academy

Definite Integrals — Topic 88 of Machine Learning Foundations

Lesson 12 - Surface Area Of Revolution In Parametric Equations

Disc method around x-axis | Applications of definite integrals | AP Calculus AB | Khan Academy
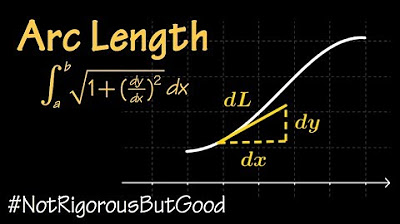
Arc Length (formula explained)
5.0 / 5 (0 votes)
Thanks for rating: