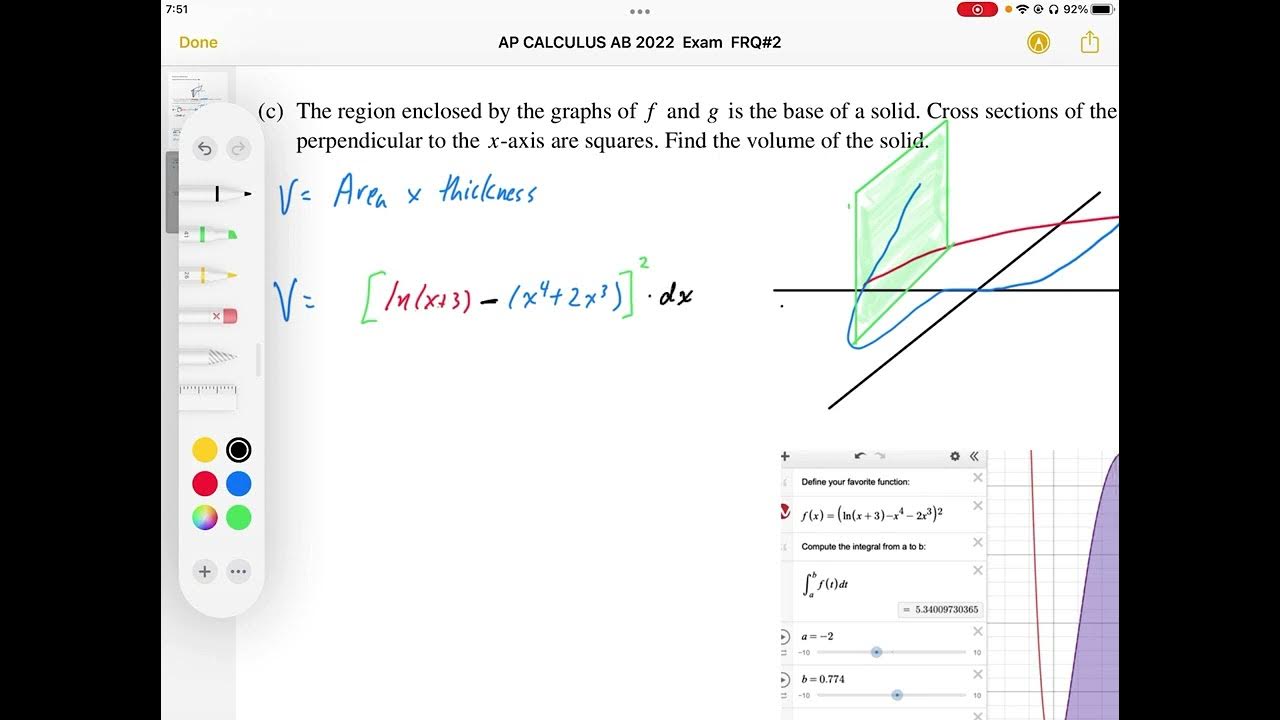
AP Calculus BC exams: 2008 1 c&d | AP Calculus BC | Khan Academy
TLDRThe video script discusses solving part c of a Calculus, BC exam problem, which involves finding the volume of a solid with cross-sections that are squares. The problem requires understanding the geometry of the solid, setting up an integral expression, and using calculus concepts to evaluate the volume. The script also touches on the use of a graphing calculator for numerical evaluation of the integral, demonstrating the process with a TI-85 emulator and yielding a result of 9.9783 cubic units for the volume of the solid. The video ends with a teaser for part d, which involves modeling the surface of a pond with varying depth.
Takeaways
- 📚 The problem discussed is part c of the first free response question from a Calculus BC exam.
- 🎲 The region r represents the base of a solid in a three-dimensional space, which is visualized with the help of a drawing.
- 📊 Cross-sections of the solid perpendicular to the x-axis are squares, with the height equal to the base length.
- 🤔 The volume of the solid is determined by calculating the area of each cross-sectional square, multiplying by an infinitesimally small change in x (dx), and summing these volumes.
- 🧩 The area of each square is found by taking the difference between the functions sin(pi x) and (x^3 - 4x), squaring the result.
- 🌠 The boundaries for the integration are given as 0 and 2, corresponding to the limits of x.
- 📈 The integral expression is set up to calculate the volume of the solid by integrating the squared difference of the functions from x=0 to x=2.
- 🔢 Analytically solving the integral is complex and time-consuming, involving power reduction formulas and integration by parts.
- 📱 A graphing calculator is recommended for numerically evaluating the definite integral, which is required for parts of the problem.
- 👨🏫 The video script provides a step-by-step guide on how to use a TI-85 emulator to input and evaluate the integral.
- 🌊 Part d of the problem introduces a new scenario where the region r models the surface of a small pond, with the depth of water given by the function h(x) = 3 - x.
- 🏞️ The video ends with a teaser for the next installment, where the volume of water in the pond will be calculated in the subsequent video.
Q & A
What is the main topic of the video?
-The main topic of the video is solving part c of the first problem on the Calculus BC exam, which involves finding the volume of a solid with cross-sections perpendicular to the x-axis.
How does the speaker redraw the region r to help with visualization?
-The speaker redraws the region r with a little perspective to help visualize it in three dimensions.
What are the two possible cross-sections mentioned in the video?
-The two possible cross-sections mentioned are those that are either perpendicular to the x-axis or parallel to the y-axis.
What is the shape of each cross-section according to the problem?
-Each cross-section is a square.
How does the speaker describe the process of finding the volume of the solid?
-The speaker describes the process as taking the area of each of the squares, multiplying them by a very small change in x (dx), and then summing up all of these infinitely thin solids to get the volume of the whole.
What is the expression for the area of each square cross-section?
-The area of each square cross-section is given by the squared difference between the top function (sin of pi x) and the bottom function (x to the third minus 4x).
What are the boundaries of integration used in the problem?
-The boundaries of integration are 0 and 2.
Why does the speaker suggest using a graphing calculator for this problem?
-The speaker suggests using a graphing calculator because the analytical solution involves complex steps like power reduction formulas in trigonometry and integration by parts, which would be very time-consuming on the AP Exam.
How does the speaker use the TI-85 emulator to solve the integral?
-The speaker uses the calculus function on the TI-85 emulator, inputs the expression for the area of the squares, specifies x as the independent variable, and sets the integration boundaries from 0 to 2.
What is the calculated volume of the solid?
-The calculated volume of the solid is approximately 9.9783 cubic units.
What is the application of the problem discussed at the end of the video?
-The application discussed at the end of the video is that the region r models the surface of a small pond, where the depth of the water at any point x from the y-axis is given by h of x equals 3-x.
How does the speaker plan to continue the discussion?
-The speaker plans to continue the discussion in the next video, where they will address the volume calculation for the pond modeled by the region r.
Outlines
📚 Calculus Problem: Volume of a Solid with Square Cross-Sections
The paragraph begins with the discussion of a free response part c of the first problem on the Calculus, BC exam. The problem involves a solid with a base region r and cross sections perpendicular to the x-axis that are squares. The challenge is to visualize the solid in three dimensions and calculate its volume. The speaker explains the process of finding the volume by multiplying the area of each square (which is the difference between two functions) by a very small change in x (dx). The integral expression for the volume is set up, but due to its complexity, the speaker suggests using a graphing calculator to numerically evaluate the definite integral. The TI-85 emulator is used to perform the calculation, and the resulting volume of the solid is found to be 9.9783 cubic units.
🌊 Pond Volume Calculation using Depth Function
In this paragraph, the speaker transitions to discussing part d of the exam problem, which involves a pond modeled by the region r. The depth of the pond's water at any point x from the y-axis is given by the function h(x) = 3 - x. The speaker describes how the depth changes across the pond, with the water getting shallower as one moves to the right. The goal is to calculate the volume of the pond. The speaker sets up the problem by visualizing the cross-section along the x-axis and recognizing the depth at x = 2 to be 1 unit. However, the speaker notes the difficulty in visualizing the entire volume and decides to continue the calculation in the next video, leaving the problem partially solved.
Mindmap
Keywords
💡Calculus
💡Cross-section
💡Solid
💡Integration
💡Graphing Calculator
💡Volume
💡Functions
💡Pond
💡Depth
💡Trigonometry
💡Power Reduction Formulas
Highlights
The problem discussed is part c of the first problem on the Calculus, BC exam, focusing on finding the volume of a solid.
The solid's base is the region r, which is visualized in three dimensions for better understanding.
Cross-sections of the solid are perpendicular to the x-axis, and each cross-section is a square.
The volume of the solid is determined by calculating the area of the squares and multiplying by an infinitesimally small change in x (dx).
The area of each square is found by taking the difference between two functions, squaring the result, and then integrating over the given interval.
The top function is sin(pi x), and the bottom function is y = x^3 - 4x, which are used to calculate the base of the squares.
The boundaries for the integration are given as 0 and 2, which are straightforward and correspond to the limits of the region r.
An analytical approach to the problem is discussed, but it is noted to be very complex and time-consuming due to the need for power reduction formulas and integration by parts.
A graphing calculator is recommended for its efficiency in numerically evaluating definite integrals, making it suitable for solving the problem within a limited time frame.
The TI-85 emulator is used to demonstrate how to input the integral expression and boundaries for the calculator to evaluate the volume of the solid.
The integral expression involves squaring the difference between sin(pi x) and the polynomial function, then integrating with respect to x from 0 to 2.
The calculated volume of the solid is approximately 9.9783 cubic units, showcasing the practical application of numerical integration.
The transcript also discusses part d of the problem, which models the surface of a small pond with varying depth.
The depth of the pond is given by the function h(x) = 3 - x, which decreases as x increases.
The challenge in part d involves visualizing the shape of the pond's cross-section and calculating its volume based on the given depth function.
The video concludes with a mention of continuing the problem in the next video, indicating a series of educational content.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: