Chaos theory and geometry: can they predict our world? – with Tim Palmer
TLDRThe speaker discusses chaos theory, a fundamental concept in 20th-century physics, which explores how simple systems can exhibit complex and unpredictable behavior. Through demonstrations with pendulums and the Lorenz model, the talk highlights the intricate dance between predictability and chaos, and how this theory applies to various fields, including weather prediction and quantum mechanics. The speaker also delves into the philosophical implications of Bell's experiment, suggesting that our understanding of quantum mechanics and reality itself may require a radical new approach that considers the universe as a deterministic but non-computable system.
Takeaways
- 🌀 Chaos theory, a significant 20th-century physics theory, explains how simple systems can exhibit complex and unpredictable behavior.
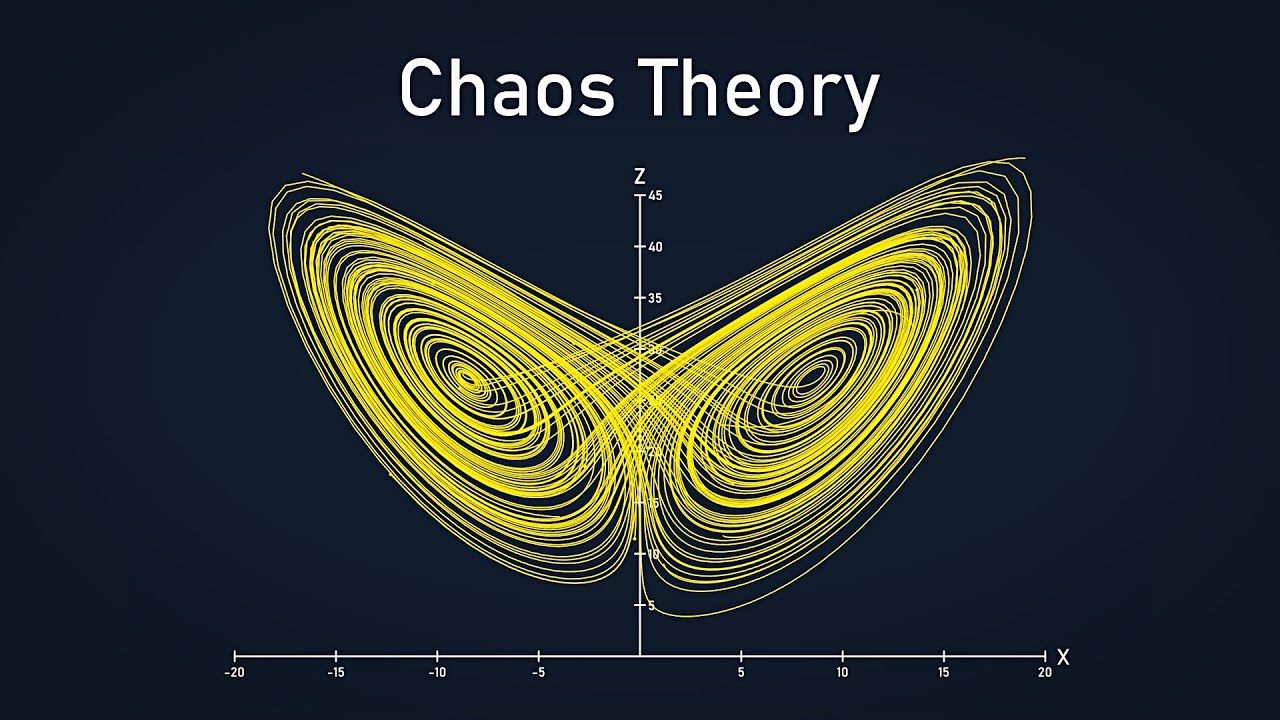
- 🔄 The Lorenz attractor demonstrates the fractal nature of chaos, where small changes in initial conditions can lead to vastly different outcomes, indicating a deterministic but non-computable system.
- 📊 The speaker uses the metaphor of buying trousers to introduce the concept of state space, where each parameter (like leg length, waist size, and color) represents a dimension in an abstract space.
- 🤔 The unpredictability of chaotic systems is related to the long-term prediction of outcomes, but certain states can be more predictable than others depending on initial conditions.
- 🌪️ The concept of fractal geometry links the mathematics of the 20th century, such as Kurt Godel's incompleteness theorems, Alan Turing's work on computation, and Andrew Wiles' proof of Fermat's Last Theorem.
- 🔮 The speaker suggests that fractal geometry could be a bridge between classical physics and quantum mechanics, potentially aiding in the unification of these theories.
- 🌍 The practical applications of chaos theory include improving weather forecasting and disaster preparedness, demonstrating the theory's relevance to daily life.
- 💡 The Bell experiment, which suggests non-locality and indeterminism in quantum mechanics, can be interpreted differently when considering the universe as a deterministic dynamical system on a fractal attractor.
- 🌟 The speaker proposes that understanding quantum gravity might require a new theory as revolutionary as general relativity was to Newtonian gravity, hinting at the importance of considering global structures in physics.
- 📚 The Nobel Prize-winning work of Suki Manabe and others is highlighted as evidence that the principles discussed are influential in the field of physics.
Q & A
What is chaos theory and how does it relate to the unpredictability of complex systems?
-Chaos theory is a branch of physics that describes how simple systems can exhibit complex and unpredictable behavior. It tries to make sense of what appears to be chaotic by showing that underlying simple dynamics can lead to complex and seemingly random outcomes. This theory is crucial for understanding the inherent unpredictability in certain complex systems, such as weather patterns or the motion of celestial bodies.
How do pendulums demonstrate the principles of chaos theory?
-Pendulums, particularly those with more complex configurations like the one with two pivots or the one with magnets, can demonstrate chaos theory by showing how small changes in initial conditions can lead to vastly different outcomes. These pendulums can move in highly irregular patterns that are extremely difficult to predict, illustrating the sensitivity to initial conditions which is a hallmark of chaotic systems.
Who discovered the Lorenz attractor and what is its significance?
-The Lorenz attractor was discovered by Edward Lorenz, an American mathematician and meteorologist. Its significance lies in its representation of a set of differential equations that describe the behavior of a chaotic system. The Lorenz attractor's butterfly shape is an example of a fractal, which is a complex geometric pattern that repeats at different scales, and it has become an iconic symbol in the study of chaos theory.
What is the connection between fractal geometry and the three major theorems of 20th-century mathematics mentioned in the script?
-The connection between fractal geometry and the three major theorems of 20th-century mathematics (Gödel's incompleteness theorems, Turing's work on computability, and Wiles' proof of Fermat's Last Theorem) is that they all, in some way, deal with the boundaries of what can be known or proven within a mathematical system. Fractal geometry, with its infinite complexity and self-similarity, provides a visual and conceptual framework for understanding these theorems, which challenge traditional notions of mathematical certainty and completeness.
How does the concept of state space relate to the discussion on chaos theory?
-State space is a crucial concept in chaos theory as it represents the set of all possible states a system can be in. Each point in the state space corresponds to a particular configuration of the system. The trajectory of a point through state space over time represents the evolution of the system. In chaotic systems, these trajectories can be highly unpredictable and sensitive to initial conditions, even though they are determined by simple underlying rules.
What is the practical significance of chaotic systems in weather prediction?
-The practical significance of chaotic systems in weather prediction lies in the understanding that while short-term predictions can be relatively accurate, long-term forecasts become increasingly uncertain due to the inherent unpredictability of chaotic dynamics. This has led to the use of ensemble forecasting, where multiple forecasts with slightly different initial conditions are made to provide a range of possible outcomes and to estimate the likelihood of different weather events.
How does the concept of fractal geometry challenge traditional Euclidean geometry?
-Fractal geometry challenges traditional Euclidean geometry by introducing structures that are infinitely complex and self-similar at all scales. Unlike Euclidean shapes, which become simple and predictable when zoomed in, fractals like the Lorenz attractor maintain their complexity and exhibit intricate patterns without ever becoming boring or repetitive. This introduces a new level of geometric understanding that is fundamentally different from the traditional Euclidean concepts of spheres, ellipses, and other regular shapes.
What is the Bell experiment and why is it significant in physics?
-The Bell experiment is a series of tests designed to verify the predictions of quantum mechanics regarding the correlations between entangled particles. It is significant because it appears to demonstrate phenomena such as quantum entanglement and nonlocality, which challenge classical notions of locality and realism in physics. The experiment has profound implications for our understanding of the fundamental nature of reality and has led to debates about the interpretation of quantum mechanics.
How does the speaker propose that fractal geometry could change our approach to understanding the universe?
-The speaker suggests that fractal geometry could lead to a new understanding of the universe as a deterministic dynamical system evolving on a fractal attractor. This perspective emphasizes the importance of global properties and large-scale structures, potentially leading to a top-down approach that complements the traditional bottom-up method of understanding physics. It challenges reductionism and suggests that the unification of quantum mechanics and gravity may require considering the universe's largest structures as much as its smallest.
What is the speaker's view on the potential applications of ensemble forecasting?
-The speaker believes that ensemble forecasting, which involves running multiple simulations with slightly different initial conditions, has significant practical applications beyond weather prediction. He suggests that it could be used to predict and prepare for a variety of events, including conflicts, pandemics like COVID-19, and economic fluctuations. The speaker sees ensemble forecasting as a tool for understanding and potentially mitigating the impacts of chaotic systems.
Outlines
🌀 Introduction to Chaos Theory
The speaker introduces chaos theory as a significant theory of the 20th century, highlighting its role in explaining complex and unpredictable motions within relatively simple systems. The talk emphasizes the importance of understanding chaos theory in the context of physics and its applications, such as pendulum demonstrations, to illustrate the concepts of chaos and unpredictability.
📐 Euclidean vs. Fractal Geometries
The speaker contrasts traditional Euclidean geometry with fractal geometries, noting that while Euclidean shapes become boring upon closer inspection, fractals reveal increasingly complex structures. The talk suggests that fractal geometry bridges the gap between classical mathematics and modern mathematical breakthroughs, and may even explain complex experiments like the Bell experiment.
🌐 State Space and Fractal Attractors
The concept of state space is introduced as a critical concept in understanding chaos theory. The speaker uses the analogy of buying trousers to explain how state space represents different parameters of a system. The talk then delves into the Lorenz equations and their depiction of state space, highlighting the discovery of fractal attractors and their significance in chaotic systems.
🔍 Exploring Cantor's Set and Its Implications
The speaker describes Cantor's Set as a foundational element of chaotic geometry, explaining its construction through the iterative process of removing the middle third of a line. The talk emphasizes the counterintuitive nature of Cantor's Set, which has no size yet contains an infinite number of points, and its relevance to the geometry seen in chaotic equations.
🔗 Linking Fractal Geometry to Mathematical Theorems
The speaker establishes a connection between fractal geometry and significant theorems in mathematics, such as Hilbert's Decision Problem and Fermat's Last Theorem. The talk highlights the work of mathematicians like Turing and Wiles, and how the geometric properties of fractal attractors can be used to formulate problems that are algorithmically uncomputable.
🌪️ Predictability in Chaotic Systems
The speaker discusses the predictability of chaotic systems, emphasizing that it depends on the initial conditions. The talk uses the Lorenz attractor to illustrate how certain states can be highly predictable, while others are not. The speaker also shares their work on ensemble forecasting in weather prediction, showing how multiple forecasts with slightly varied initial conditions can help determine the predictability of a system.
🌍 Applications of Chaos Theory in Disaster Preparedness
The speaker explores the practical applications of chaos theory in disaster preparedness, particularly in predicting extreme weather events like hurricanes. The talk introduces the concept of anticipatory action, where humanitarian agencies use ensemble forecasts to efficiently allocate resources before disasters strike, based on the probability of an event occurring.
🌡️ Climate Change and Chaotic Weather Systems
The speaker addresses the skepticism around climate change by explaining that while weather is chaotic, climate change involves understanding changes in weather statistics over time. The talk uses the analogy of a magnetic pendulum to illustrate how external factors, like carbon dioxide emissions, can shift the 'table' on which the pendulum operates, altering the probabilities of different weather states.
🏆 Nobel Prizes and the Nature of Quantum Mechanics
The speaker reflects on the significance of Nobel Prize-winning work related to chaos theory and quantum mechanics. The talk mentions the 2021 Nobel Prize for climate models and the 2022 Nobel Prize for the Bell experiment, which challenged traditional notions of reality and locality in quantum physics. The speaker suggests that understanding quantum mechanics may require a new theory as revolutionary as general relativity was to Newtonian gravity.
📚 Conclusion: The Future of Physics and Reductionism
The speaker concludes by suggesting that the future of physics may lie in understanding the universe as a whole, rather than solely focusing on its smallest parts. The talk posits that fractal attractors and the non-computable nature of chaotic systems could lead to a new understanding of quantum gravity, potentially shifting away from the reductionist approach that has dominated scientific thinking.
Mindmap
Keywords
💡Chaos Theory
💡Fractal Geometry
💡Predictability
💡Entanglement
💡Bell Experiment
💡State Space
💡Non-Computable
💡Reductionism
💡Deterministic
💡Quantum Mechanics
Highlights
Chaos theory is one of the great theories of 20th century physics, describing how simple systems can exhibit complex and unpredictable behavior.
The Royal Institution staff helped create pendulum demonstrations to illustrate chaos theory, showing the complex motion of pendulums with multiple pivots and those with magnets.
Ed Lorenz's equations, developed to model weather, are a key example of how classical mathematics can generate fractal geometries that Newton would not have recognized.
Fractal geometries, such as those generated by Lorenz equations, provide a bridge between classical mathematics and 20th century mathematical discoveries.
The geometry of chaos may be the missing ingredient in the quest to unify quantum mechanics and general relativity into a single theory.
Kurt Godel, Alan Turing, and Andrew Wiles are highlighted as three of the greatest 20th century mathematicians whose work connects to fractal geometry.
The concept of state space is introduced as a critical idea in understanding the behavior of chaotic systems and their predictability.
The Lorenz attractor, a fractal, demonstrates the structure of chaotic systems and how they evolve over time.
The predictability of chaotic systems depends on initial conditions, and ensemble forecasting can help determine the level of predictability in weather patterns.
The practical applications of chaos theory include improving disaster preparedness and humanitarian aid distribution based on ensemble forecasts.
The Bell experiment, awarded the 2022 Nobel Prize, challenges our understanding of reality and locality in quantum mechanics.
The universe may be a deterministic dynamical system evolving on a fractal attractor, suggesting a new perspective on unifying quantum mechanics and gravity.
Roger Penrose suggests that understanding quantum non-locality may require a radical new theory as different from quantum mechanics as general relativity was from Newtonian gravity.
The idea of a deterministic but non-computable quantum gravity theory is proposed, which aligns with the non-computable nature of fractal attractors.
The lecture concludes with a call for a top-down approach to understanding the laws of physics, focusing on the largest structures of the universe as well as the smallest scales.
Transcripts
Browse More Related Video
Chaos Theory: the language of (in)stability

What If Physics IS NOT Describing Reality?

The EPR Paradox & Bell's inequality explained simply

Chaos: The Science of the Butterfly Effect

Gordon Belot: The Wave Function for Primitive Ontologists

Einstein's Quantum Physics Theory That Proved Him Wrong | The Secrets Of Quantum Physics | Spark
5.0 / 5 (0 votes)
Thanks for rating: