Chaos: The Science of the Butterfly Effect
TLDRThe video explores the concept of the butterfly effect, which suggests that minor causes can lead to significant outcomes. Originating from a scientific paper, the idea has permeated pop culture, symbolizing how small choices can have vast consequences. The video delves into the history of predictability in science, from Newton's laws to the realization of chaos theory. It explains deterministic systems like pendulums using phase space, contrasting them with chaotic systems like the weather, which are sensitive to initial conditions. The video highlights Ed Lorenz's discovery of chaos through simplified weather models and the resulting unpredictability. It also touches on the unpredictability of the solar system and the inherent limits of forecasting chaotic systems. Despite this, the video points out the underlying structure and beauty in chaotic systems, such as the Lorenz attractor. Sponsored by LastPass, a password manager that auto-generates strong, unique passwords for each site, reducing the risk associated with password reuse—a modern application of the butterfly effect in cybersecurity.
Takeaways
- 🦋 The butterfly effect suggests that small causes can lead to significant outcomes, capturing the public imagination with numerous pop culture references.
- 📜 The concept originates from a scientific paper and questions the predictability of the future, which is a fundamental human inquiry.
- ⚙️ Newton's laws made the universe seem predictable, but the idea of determinism was challenged by the three-body problem and later by chaos theory.
- 🧲 Laplace's demon is a hypothetical entity that, if it knew the universe's current state, could predict the future, representing total determinism.
- 🌌 Quantum mechanics introduces uncertainty, but on a scale too small to affect human-sized problems, initially suggesting a deterministic world view.
- 📈 Phase space is a graphical representation of all possible states of a dynamical system, like a pendulum, showing how it evolves over time.
- 🔄 The three-body problem and the work of Henri Poincaré revealed the complexity and unpredictability in seemingly simple systems.
- ☕ Ed Lorenz's discovery of sensitive dependence on initial conditions while simulating weather led to the formalization of chaos theory.
- 🌀 Lorenz's simplified model, despite being deterministic, showed that minor differences in initial conditions could lead to vastly different outcomes, a key characteristic of chaos.
- 🌡 Weather prediction is inherently limited by chaos, with forecasts becoming less reliable over time, leading to ensemble forecasting methods.
- 🔮 Chaotic systems are deterministic yet unpredictable in practice due to the impossibility of knowing initial conditions with infinite precision.
- 🛍️ LastPass is a password manager that auto-generates strong, unique passwords for each site, enhancing online security and reducing the risk of a 'butterfly effect' in data breaches.
Q & A
What is the 'butterfly effect' in the context of the video?
-The butterfly effect refers to the concept that small causes, such as the flap of a butterfly's wings, can lead to significant effects, like the triggering of a tornado. It is a part of chaos theory and is often used to illustrate how minor actions or decisions can have far-reaching, unpredictable consequences.
What is the significance of the scientific paper mentioned in the video?
-The scientific paper mentioned is significant because it introduced the concept of the butterfly effect. It was published nearly 50 years ago and has had a profound impact on public imagination, leading to widespread references in popular culture.
How did Isaac Newton's laws of motion and universal gravitation contribute to the idea of predictability?
-Newton's laws provided a framework that allowed for the precise explanation and prediction of the motions of celestial bodies, such as planets and moons. This led to the belief that if the current state of the universe was known, the future could be predicted with certainty, a concept known as determinism.
What is Laplace's demon and how does it relate to determinism?
-Laplace's demon is a hypothetical super-intelligent being that knows the current state of the universe, including the positions and momenta of all particles. If this being could analyze this data, it would be able to predict the future with absolute certainty. This thought experiment by Pierre-Simon Laplace encapsulates the idea of total determinism.
What is the phase space representation in dynamical systems?
-Phase space is a way to graphically represent every possible state of a dynamical system. For a simple pendulum, it could be a plot with the angle of the pendulum on the x-axis and its velocity on the y-axis. This allows for a visual representation of how the system evolves over time, including its tendency towards certain states, known as attractors.
How does the three-body problem challenge Newtonian physics?
-The three-body problem refers to the difficulty in predicting the motion of three or more bodies interacting with each other gravitationally. While the motion of two bodies, like the Earth and the Sun, can be calculated, adding a third body, such as the Moon, makes the calculations extremely complex and essentially unsolvable with Newtonian physics alone.
What is the significance of Ed Lorenz's work on weather simulation?
-Ed Lorenz's work was significant because it revealed the concept of sensitive dependence on initial conditions, which is a key characteristic of chaotic systems. His experiments with simplified weather models showed that even tiny differences in starting conditions could lead to dramatically different outcomes, highlighting the unpredictability inherent in such systems.
How does the Lorenz attractor illustrate the structure within chaos?
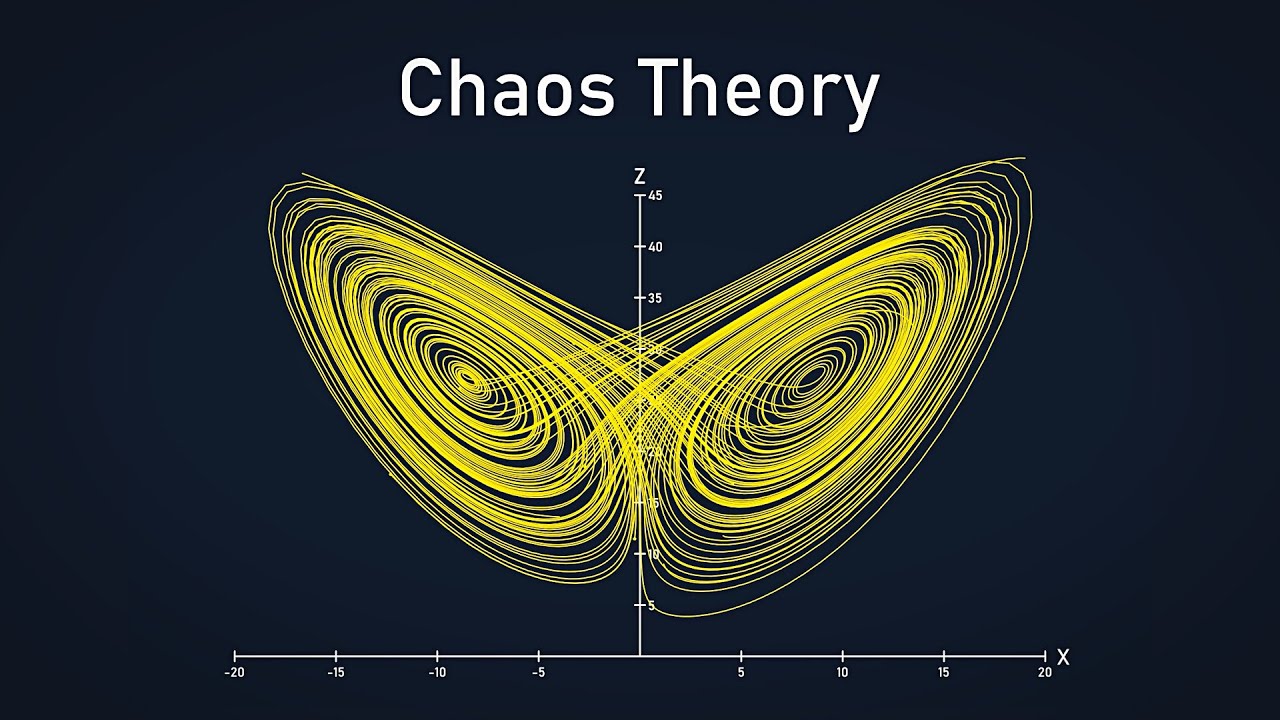
-The Lorenz attractor is a set of points towards which the system's state tends to evolve, regardless of the initial conditions. It has a butterfly-like shape and shows that while individual trajectories are unpredictable, the overall behavior of the system is constrained to this shape, revealing an underlying order within the chaos.
Why is weather forecasting so challenging, even with advanced technology?
-Weather forecasting is challenging because the Earth's atmosphere is a chaotic system. Small errors in the initial conditions can lead to vastly different forecasts. This sensitivity to initial conditions means that beyond a certain time frame, typically about a week, the accuracy of weather predictions significantly decreases.
What is an ensemble forecast and how does it improve weather prediction?
-An ensemble forecast is a method used by meteorologists where multiple simulations are run with slightly varying initial conditions and model parameters. This approach provides a range of possible outcomes, which can give a more comprehensive view of the potential weather scenarios, improving the reliability of predictions.
How does the concept of the butterfly effect relate to password security?
-The concept is used metaphorically to illustrate how a small action, like using the same password across multiple accounts, can lead to significant consequences if one account is compromised. LastPass, a password manager, helps prevent this by generating strong, unique passwords for each site, reducing the risk associated with password reuse.
What are the benefits of using a password manager like LastPass?
-LastPass offers unlimited password storage, auto-generation of strong passwords, and free cross-device sync. It eliminates the need to remember or write down passwords, reduces the risk of account lockouts and password resets, and can enhance security with features like multi-factor authentication.
Outlines
🌀 The Butterfly Effect and Determinism
This paragraph introduces the concept of the butterfly effect, which suggests that small causes can lead to significant outcomes. It references the scientific paper that originated the idea and its widespread influence in popular culture. The paragraph also discusses the historical perspective on predictability, from Newton's laws to Laplace's demon, illustrating the concept of determinism where the future is seen as fixed and predictable. It touches on the role of quantum mechanics and the uncertainty principle, then transitions into a discussion on dynamical systems and phase space using the example of a simple pendulum. The summary concludes with the mention of the three-body problem and the onset of chaos theory.
🔍 Sensitive Dependence and Chaos Theory
The second paragraph delves into the discovery of chaos theory through the work of meteorologist Ed Lorenz. It describes how Lorenz's attempt to rerun a computer simulation with slightly rounded initial conditions led to dramatically different outcomes, highlighting the sensitive dependence on initial conditions. Lorenz's simplification of his model to a system with three variables still exhibited chaotic behavior. The summary explains how this sensitivity leads to a lack of predictability and contrasts it with deterministic but non-chaotic systems like a pendulum. It also discusses the practical implications for weather forecasting and the adoption of ensemble forecasts. The paragraph concludes with examples of other chaotic systems, including the double pendulum and even our solar system, emphasizing the inherent unpredictability and limits of prediction in such systems.
🦋 The Lorenz Attractor and the Structure of Chaos
The final paragraph discusses the silver lining of chaos theory: the discovery of underlying structure and patterns, such as the Lorenz attractor. It explains how, despite the initial randomness, points in phase space for Lorenz's system tend towards a butterfly-shaped attractor, indicating a large set of states that the system can evolve into. The summary highlights the contrast between the unpredictability of individual trajectories and the collective behavior of the system. It also touches on the concept of fractals and their role in understanding the infinite complexity within a finite space. The paragraph concludes with a sponsored message about LastPass, a password manager that generates strong, unique passwords for each online account, emphasizing the importance of password diversity for online security.
Mindmap
Keywords
💡Butterfly Effect
💡Determinism
💡Phase Space
💡Three-Body Problem
💡Chaos Theory
💡Sensitive Dependence on Initial Conditions
💡Lorenz Attractor
💡Fractals
💡Ensemble Forecasting
💡LastPass
💡Heisenberg's Uncertainty Principle
Highlights
The butterfly effect is a concept that suggests small causes can lead to significant outcomes, famously illustrated by the example of a butterfly's wings in Brazil influencing a tornado in Texas.
The idea originates from a scientific paper published nearly 50 years ago and has since become a staple in popular culture, with numerous movies, TV episodes, and short films referencing it.
The butterfly effect raises fundamental questions about the predictability of the future and our ability to forecast it.
In the late 1600s, the development of Newton's laws of motion and universal gravitation led to the belief that the universe was predictable.
Pierre-Simon Laplace's thought experiment introduces the concept of determinism, where a super-intelligent being could predict the future by knowing the current state of the universe.
Heisenberg's uncertainty principle from quantum mechanics introduces a level of unpredictability, but its impact is negligible when considering larger scales relevant to humans.
Phase space is introduced as a method to represent the possible states of a dynamical system, such as a pendulum, using position and velocity.
A simple pendulum without friction exhibits periodic and predictable motion, represented in phase space as a closed loop.
The three-body problem, which involves calculating the motion of three celestial bodies, is identified as a complex issue that Newton himself found challenging.
Henri Poincaré's work on the three-body problem led to the discovery of chaos theory, highlighting the unpredictability in certain systems.
Ed Lorenz's weather simulation experiments in the 1960s revealed that tiny differences in initial conditions could lead to dramatically different outcomes, a phenomenon known as sensitive dependence on initial conditions.
Lorenz's simplified model, involving three variables, demonstrated chaotic behavior where the system never revisits the same state, highlighting the unpredictability of such systems.
Chaotic systems, despite being deterministic, are unpredictable in practice due to the impossibility of knowing initial conditions with infinite precision.
The difficulty of predicting weather more than a week in advance is attributed to the chaotic nature of the Earth's atmosphere.
Ensemble forecasting, which involves varying initial conditions and model parameters, is now used by meteorologists to create a set of predictions instead of a single forecast.
Chaotic systems are found in various contexts, from the double pendulum to the solar system, indicating unpredictability even in systems considered orderly.
The Lorenz attractor, a fractal structure, represents the set of states towards which a chaotic system evolves, despite the unpredictability of individual trajectories.
LastPass, a password manager, is highlighted for its ability to auto-generate strong, unique passwords for each website, promoting security and reducing the risk of a single breach affecting multiple accounts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: