Trigonometry - Easy to understand 3D animation

Physics Videos by Eugene Khutoryansky
5 Mar 201516:29
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the fundamentals of trigonometry, highlighting its critical role in science and technology. It introduces the concepts of sine and cosine through a unit circle, explaining how they relate to angles and their applications in physics and engineering. The video also explores radians, the Law of Cosines, and the Law of Sines, emphasizing their universal applicability. Furthermore, it touches on inverse functions and the creation of complex waveforms through the combination of sine and cosine waves, illustrating the profound impact of trigonometry on understanding the universe.

Takeaways
  • 🧮 Mathematics is the foundation of all science and technology, with trigonometry being a crucial branch.
  • 📏 Trigonometry is essential for understanding physics and engineering, impacting how we perceive and interact with the world.
  • 🔄 The concept of measuring angles in radians is introduced through the circumference of a circle, offering a more natural unit of angle measurement in mathematics.
  • 📐 Cosine and sine functions are defined as the X and Y coordinates of a point on a circle with radius 1, illustrating the relationship between angles and side lengths in a right triangle.
  • 🔢 Sine and cosine values range between -1 and +1, reflecting their geometric significance in the unit circle.
  • 📲 Calculators use sine, cosine, and their inverses to translate between angles and side ratios, facilitating problem-solving in various fields.
  • ✈️ Sine and cosine functions have practical applications in navigation and physics, enabling precise calculations in three-dimensional space.
  • ⚖️ The Law of Cosines generalizes the Pythagorean Theorem, accommodating any triangle, not just right-angled ones.
  • 🌊 Sine and cosine waves can be combined to form any function, showcasing their fundamental role in modeling physical phenomena and signals.
  • ∞ The concept of an angle θ can extend beyond 360 degrees and into negative values, illustrating the cyclical nature of trigonometric functions.
Q & A

  • What is the foundational branch of mathematics mentioned in the transcript?

    -The foundational branch of mathematics mentioned is trigonometry.

  • How does the absence of trigonometry affect the fields of physics and engineering?

    -Without trigonometry, our knowledge of physics and engineering would crumble, indicating its fundamental importance in these fields.

  • What is the significance of the circle with radius 1 in the context of the script?

    -The circle with radius 1 is used to define the unit circle, which is essential for understanding angles in terms of radians and for calculating trigonometric functions.

  • How is the angle θ measured from the X axis?

    -The angle θ is measured from the X axis in the counterclockwise direction, and it can be represented in degrees or radians.

  • What is the relationship between the distance traveled around the circle and the measurement of θ in radians?

    -When θ is measured based on the distance traveled around the circle, it is referred to as radians, with a full circle's circumference (π multiplied by the diameter of 2) corresponding to a θ of 2π radians.

  • What are the names given to the X and Y coordinates of the green ball traveling around the circle?

    -The X coordinate is called the 'cosine of θ' and the Y coordinate is called the 'sine of θ'.

  • What is the range of values for sine and cosine functions?

    -The sine and cosine of an angle can range anywhere between -1 and +1.

  • How can the values of sine and cosine be calculated for a given angle?

    -Calculators have sine and cosine buttons that allow you to enter the values of an angle (in degrees or radians) to find the corresponding sine and cosine values.

  • What do the 'inverse sine' and 'inverse cosine' buttons on a calculator do?

    -The 'inverse sine' and 'inverse cosine' buttons calculate the angle that would have produced a given sine or cosine value.

  • How do sine and cosine functions relate to solving problems in physics?

    -Sine and cosine functions are crucial in solving critical problems across all branches of physics, including navigation and determining angles in three-dimensional space.

  • What is the more general equation that includes the Pythagorean Theorem?

    -The more general equation that includes the Pythagorean Theorem is the 'Law of Cosines', represented as A^2 + B^2 = C^2 + 2ABcos(Ψ), where Ψ is the angle between sides A and B.

  • What are the additional relationships derived from the sine and cosine functions?

    -The additional relationships derived from the sine and cosine functions are the 'Tangent', the 'Cotangent', the 'Secant', and the 'Cosecant'.

  • How can we represent the angle θ in a three-dimensional coordinate system?

    -In a three-dimensional coordinate system, the angle θ can be represented by an axis that interacts with the X and Y axes, with θ ranging from negative infinity to positive infinity.

  • What is the implication of using sine and cosine waves in understanding physical objects?

    -By understanding how physical objects respond to sine and cosine waves, we can determine their responses to every possible function in the Universe, as any function can be created by combining sine and cosine waves of different frequencies and amplitudes.

Outlines
00:00
📐 Fundamentals of Trigonometry

This paragraph introduces the foundational role of mathematics, particularly trigonometry, in the realm of science and technology. It explains the concept of a unit circle and its relation to the angle θ, measured in degrees and radians. The paragraph further discusses the trigonometric functions sine and cosine, which represent the X and Y coordinates of a point on the unit circle, respectively. It also touches on the application of these functions in solving triangles and the use of calculators for finding trigonometric values.

05:15
🔢 Calculator Applications and Navigation

The second paragraph delves into the practical use of calculators for finding sine and cosine values for given angles, as well as their inverse functions. It highlights the significance of these functions in solving critical problems across physics and provides an example of their application in aircraft navigation. The paragraph also corrects a previous statement by introducing the Law of Cosines and the Law of Sines, which are generalizations of the Pythagorean Theorem for non-right triangles.

10:20
🌀 Exploring Advanced Trigonometric Relationships

This paragraph introduces additional trigonometric functions—tangent, cotangent, secant, and cosecant—relating to the basic sine and cosine. It discusses the concept of angles greater than 360 degrees and negative angles, representing directions beyond a single revolution around the unit circle. The paragraph also establishes the relationship between the angle θ and the coordinates on the X and Y axes, emphasizing the rotational aspect of the unit circle.

15:34
🌈 Composition of Waves and Functions

The final paragraph discusses the composition of any function through the addition of sine and cosine waves with varying frequencies and amplitudes. It emphasizes the importance of understanding how physical objects respond to these waves, as this knowledge can be applied to predict their responses to any possible function, thereby providing a comprehensive understanding of the universe's physical behavior.

Mindmap
Keywords
💡Mathematics
Mathematics is described as the foundation of all science and technology, underpinning critical advancements in fields such as physics and engineering. The script emphasizes the importance of mathematics by illustrating its application in understanding complex concepts like trigonometry, sine, and cosine functions. These mathematical principles are essential for solving real-world problems, including those encountered in engineering and physics, showcasing the pivotal role of mathematics in scientific and technological progress.
💡Trigonometry
Trigonometry is highlighted as one of the most crucial branches of mathematics, pivotal for the development of physics and engineering knowledge. The script uses trigonometry to explain how angles and circles relate to each other and introduces concepts such as sine and cosine, which are fundamental in calculating the positions and movements of objects in space. This underscores trigonometry's role in applications ranging from simple calculations to complex navigation and engineering solutions.
💡Radians
Radians are a unit of measure for angles based on the distance traveled around a circle. The script elucidates this concept by equating the circumference of a circle to π times the diameter, thus defining a full circle's rotation as 2π radians. This measurement system is essential for accurately describing angles in mathematical and physical contexts, providing a more natural approach to calculations involving circular motion and trigonometric functions than degrees.
💡Sine and Cosine
Sine and cosine are introduced as functions that represent the Y and X coordinates, respectively, of a point moving around a unit circle. These trigonometric functions vary between -1 and +1 and are crucial for calculating the positions of objects in trigonometry, physics, and engineering. The script uses these functions to demonstrate how they can be used to model physical phenomena, such as the oscillation of waves, and solve problems in various scientific fields.
💡Inverse Functions
Inverse sine and inverse cosine functions are described as tools for determining the angle that would produce a given sine or cosine value. This concept is crucial for reverse-engineering angles from known coordinates, facilitating tasks such as navigation and angle calculation in physics and engineering. The script illustrates their practical utility in calculating the necessary angles for navigating an aircraft in three-dimensional space.
💡Law of Cosines
The Law of Cosines is presented as a generalization of the Pythagorean Theorem, applicable to any triangle, not just right-angled ones. This law relates the lengths of a triangle's sides to the cosine of one of its angles, providing a fundamental principle for solving triangles. The script corrects a common misconception and clarifies that the Law of Cosines encompasses the Pythagorean Theorem as a special case, highlighting its importance in trigonometry and geometry.
💡Law of Sines
The Law of Sines is introduced as another fundamental trigonometric identity that applies to all triangles, relating the lengths of the sides to the sines of the angles. This law is essential for solving triangles when two angles and a side are known, or two sides and an angle are known, facilitating calculations in fields such as navigation, physics, and engineering. The script positions this law as equally important as the Law of Cosines, illustrating the comprehensive nature of trigonometric solutions.
💡Tangent and Cotangent
Tangent and cotangent are defined in the script as relationships between the sine and cosine of an angle, representing the ratios of opposite to adjacent sides in a right triangle. These functions are critical for understanding angles and their relationships with the sides of triangles, playing key roles in various applications of trigonometry in physics, engineering, and mathematics.
💡Secant and Cosecant
Secant and cosecant are introduced as reciprocal functions of cosine and sine, respectively. These functions extend the concept of trigonometric relationships by relating the radius of a circle to the X and Y coordinates of a point on its circumference. The script includes these relationships to showcase the diversity of trigonometric functions and their applications in solving complex mathematical and physical problems.
💡Angle Measurement
The concept of angle measurement is explored through degrees and radians, with a focus on the flexibility and universality of radians for measuring angles beyond the conventional 0 to 360-degree range. The script elaborates on how angles can be negative or exceed 360 degrees when the rotation is clockwise or multiple rotations are considered. This highlights the versatility of radians in mathematical and physical calculations, accommodating a wide range of angular measurements.
Highlights

The foundation of all science and technology is mathematics.

One of the most important branches of mathematics is trigonometry.

Without trigonometry, our knowledge of physics and engineering would crumble.

Suppose we have a circle with radius 1 placed around the center of a graph.

The angle θ, measured counterclockwise from the X axis, is fundamental in trigonometry.

θ can be measured in degrees or radians, with radians based on the distance traveled around the circle.

The circumference of a circle is π multiplied by the diameter of 2.

The X coordinate of a point on the graph represents the cosine of θ.

The Y coordinate of the same point represents the sine of θ.

Sine and cosine values range between -1 and +1.

Sine and cosine are crucial for solving critical problems in physics.

Calculators provide sine, cosine, inverse sine, and inverse cosine functions.

The Law of Cosines extends the Pythagorean Theorem for all triangles.

The Law of Sines is also universally true for all triangles.

Trigonometric relationships include Tangent, Cotangent, Secant, and Cosecant.

θ can range from negative infinity to positive infinity, including multiples of 360 degrees.

The green line represents the angle θ on the coordinate system.

Functions of any shape can be created by combining sine and cosine waves of various frequencies and amplitudes.

Understanding the response of physical objects to sine and cosine waves allows us to predict their behavior to any function.

Transcripts

Browse More Related Video

LEPT Math Majorship 2024 | Trigonometry Calculator Techniques

Trigonometry fundamentals | Ep. 2 Lockdown live math

Trigonometry: Unit Circle

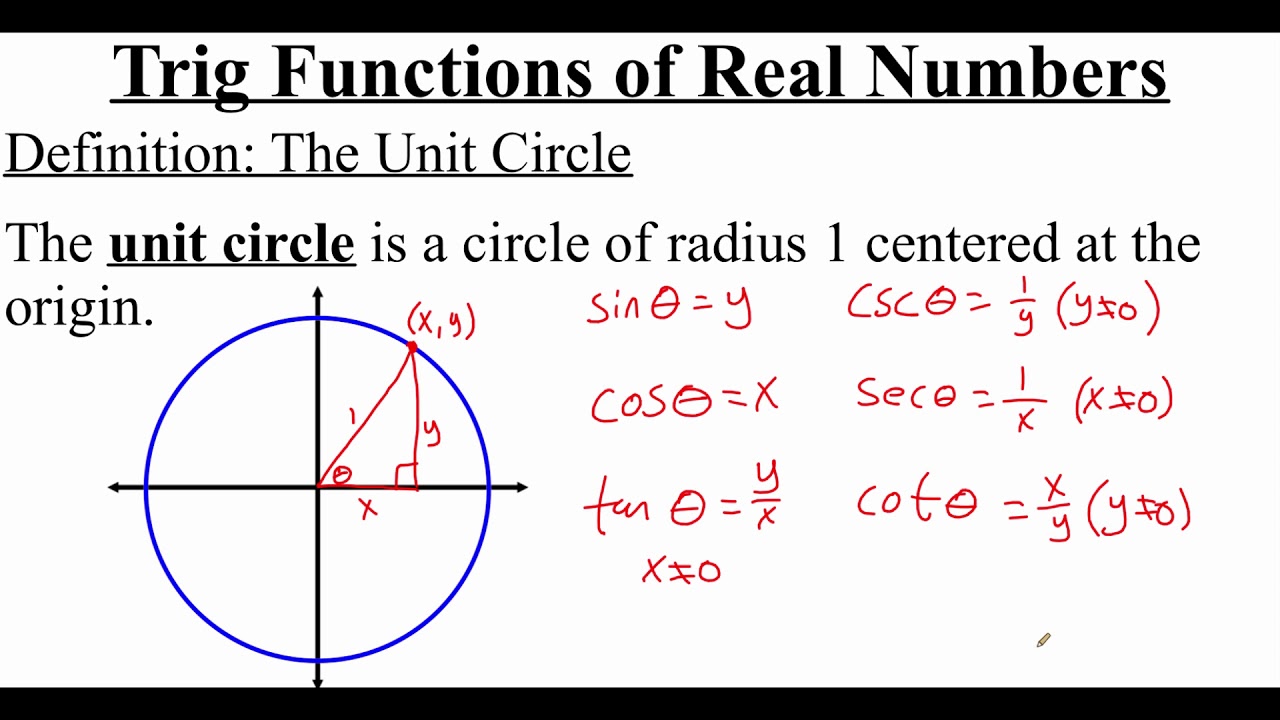
4.3.4 Trigonometric Functions of Real Numbers

The Unit Circle, Basic Introduction, Trigonometry

09 - Unit Circle - Definition & Meaning - Sin(x), Cos(x), Tan(x), - Sine, Cosine & Tangent

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryMathematicsPhysicsEngineeringSineCosineInverse FunctionsLaws of SinesLaws of CosinesNavigationWave Functions