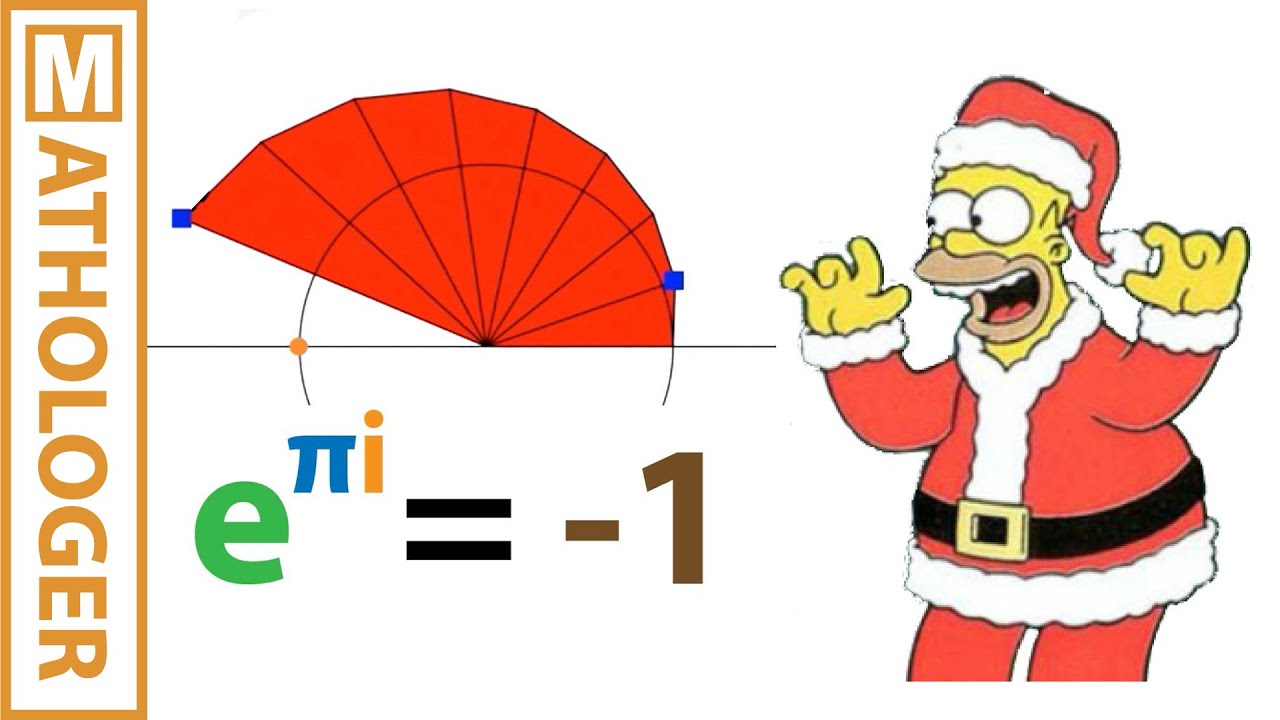Why π^π^π^π could be an integer (for all we know!).
TLDRThe video script discusses the intriguing mathematical concept of raising pi to the power of pi and whether the result is an integer. It explores the nature of transcendental numbers like pi, the limitations of current computational abilities to calculate such large numbers, and the challenges in proving the result mathematically. The script also highlights the current world records for calculating pi and the potential of Schanuel's Conjecture in providing a theoretical answer, although it remains unproven. The video is sponsored by Jane Street, emphasizing their support for the Stand Up Maths channel and their programs for those interested in mathematical careers.
Takeaways
- 🤔 The concept of 'pi to the pi' is intriguing and prompts the question of whether the result is an integer, which turns out to be a complex mathematical problem.
- 📈 Pi is a transcendental number, which means it cannot be written as a simple fraction or the solution to a neat, finite equation.
- 🔢 Transcendental numbers like pi, e, and the natural log(2) can sometimes result in integers when combined in certain mathematical operations.
- 🌐 The video mentions Tim Gowers, a renowned mathematician, who also initially thought of calculating 'pi to the pi' but realized it's not feasible.
- 🧠 Raising an irrational number to the power of another irrational can yield a rational result, as demonstrated by the example of root(2) to the power of root(2).
- 🔍 Calculating 'pi to the pi' is practically impossible due to the sheer size of the numbers involved and the current limits of computational power.
- 🏆 The current world record for calculating the most digits of pi stands at 50 trillion digits, which is far from the number of digits needed for 'pi to the pi'.
- 🛠️ Even with approximations, accurately calculating 'pi to the pi' is challenging because pi has infinitely many digits and we can only know a finite number of them.
- 📚 Schanuel's Conjecture is mentioned as a potential mathematical tool to address questions about transcendental numbers, but it remains unproven after decades.
- 🎥 The video was sponsored by Jane Street, a company known for its programs that offer opportunities in solving complex problems in the financial sector.
- 🎓 The Stand Up Maths channel encourages viewers, especially students and job seekers, to explore the programs offered by Jane Street for career development.
Q & A
What was the main topic of the video?
-The main topic of the video was the mathematical concept of raising pi to the power of pi and whether the result is an integer, and why it's challenging to calculate or prove.
Who was the first person to respond to the idea of calculating pi to the pi?
-Tim Gowers, a Fields Medal mathematician, was the first person to respond to the idea of calculating pi to the pi.
What are the three categories of numbers mentioned in the video?
-The three categories of numbers mentioned are integers, rationals, and irrationals.
What is a transcendental number?
-A transcendental number is a real number that is not the root of any non-zero polynomial equation with rational coefficients, such as pi, e, and the natural log of 2.
How did the video demonstrate that irrational numbers can lead to a rational result when raised to powers?
-The video showed that by raising the square root of 2 to the power of the square root of 2 and then raising that result to the power of the square root of 2 again, you eventually get the number 2, which is rational.
What is the current world record for calculating the digits of pi?
-The current world record for calculating the digits of pi is 50 trillion digits, achieved by Timothy in 2020.
Why can't we calculate pi to the pi to the pi to the pi exactly?
-We can't calculate pi to the pi to the pi to the pi exactly because the number of digits required is in the billions of billions, which is a million times more digits than what we can currently compute, and we only know a finite number of digits of pi.
What is Schanuel's Conjecture mentioned in the video?
-Schanuel's Conjecture is a mathematical proposition that makes statements about the transcendental nature of certain numbers and their combinations, but it is complex and has not been proven.
What is the significance of the video's title being 'irrational'?
-The title being 'irrational' signifies the unexpected and counterintuitive nature of the mathematical concepts discussed, particularly the fact that operations involving irrational numbers can sometimes yield rational results.
How does the video relate to potential job opportunities?
-The video relates to job opportunities by mentioning that Jane Street, the sponsor of the Stand Up Maths channel, offers various programs for university students and those seeking careers in solving complex mathematical problems in the financial world.
What was the humorous element in the video regarding the audience's reaction?
-The humorous element was the audience's reaction to the conclusion that pi to the pi to the pi to the pi is 'just a bit irrational,' which led to them booing, and the speaker jokingly threatening to send them back for a refund.
Outlines
🤔 The Mystery of Pi to the Power of Pi
The video begins with a discussion on the intriguing mathematical problem of whether pi to the power of pi equals an integer. It introduces the topic with a humorous tone, questioning the validity of such a claim. The video is sponsored by Jane Street, a company with programs for those interested in jobs in mathematics. The speaker acknowledges the immediate thought of calculating the value to verify the claim, a thought shared by renowned mathematician Tim Gowers. However, it's revealed that this calculation is impossible due to the nature of pi being a transcendental number. The speaker then delves into the classification of numbers, distinguishing between integers, rationals, irrationals, and transcendental numbers, setting the stage for a deeper exploration of the problem.
🧮 Power-Tower Calculations and the Limits of Computation
This paragraph explains the process of calculating power-towers, starting from the top and working downwards. It uses the number 3 as a placeholder for pi to illustrate the concept, showing that the numbers involved become incredibly large very quickly. The speaker contrasts the known world record for calculating pi (31 trillion digits) with the astronomical number of digits required for pi to the power of pi (almost a billion billion digits). The challenges of computation are highlighted, including the need for exact values of pi and the limitations of using approximations. The speaker also discusses the difficulty of the last step in the calculation, where the exact value of pi is crucial, and the current inability to perform such extensive computations.
🔢 The Truncation of Pi and its Impact on Calculations
The speaker presents a series of experiments and observations on the impact of truncating pi during calculations. It is found that if you raise a truncation of pi to a power that is twice the number of digits in the approximation, no decimal places in the answer will match the true value. This highlights the need for an incredibly precise approximation of pi to obtain an accurate result. The speaker also discusses the limitations of current computational methods and the vast number of decimal places needed to achieve a sufficiently accurate outcome. The paragraph concludes with the admission that we cannot currently calculate or prove whether pi to the power of pi is an integer, pointing to the limitations of our mathematical tools and the potential relevance of Schanuel's Conjecture.
🎥 Sponsorship and Conclusion of the Mathematical Discussion
The video concludes with a return to the sponsorship by Jane Street, emphasizing their support for the Stand Up Maths channel and their range of programs for those interested in mathematics and the financial world. The speaker encourages viewers to explore these opportunities and appreciates Jane Street's contribution to making the channel possible. The video ends with a mention of the Stand Up Maths production and a canned studio audience, wrapping up the mathematical discussion with a touch of humor.
Mindmap
Keywords
💡Transcendental numbers
💡Irrational numbers
💡Rational numbers
💡Power-tower
💡Schanuel's Conjecture
💡Computational complexity
💡Fields medal
💡Jane Street
💡Approximation
💡Mathematical conjecture
Highlights
The video explores the surprising concept of raising pi to the power of pi and whether the result is an integer.
The idea was sparked by a tweet that caught the attention of Tim Gowers, a Fields Medallist mathematician.
Pi is a transcendental number, which makes the possibility of it resulting in an integer when raised to itself surprising.
Rational numbers include integers and can be written as fractions, while irrationals cannot be expressed as fractions but can be solutions to equations.
Transcendental numbers like pi, e, and the natural log of 2 cannot be written as solutions to finite equations and require infinite series for their representation.
The video demonstrates that raising an irrational number to the power of another irrational can result in a rational number, and even an integer.
The video humorously suggests setting pi equal to 3 for simplicity, but emphasizes the importance of working from the top down in power-towers.
Calculating pi to the pi to the pi to the pi is practically impossible due to the sheer number of digits involved.
The current world record for calculating digits of pi is 50 trillion digits, achieved by Timothy in 2020.
The video explains the limitations of using approximations of pi in calculations, as the accuracy decreases significantly with each step.
A rough conjecture suggests that raising a truncation of pi to a power twice the number of digits in the approximation results in no correct decimal places in the answer.
The video highlights the lack of mathematical tools to prove whether pi to the power of pi is transcendental or not.
Schanuel's Conjecture offers a glimmer of hope for proving the transcendental nature of certain combinations of numbers, but it remains unproven after decades.
The video concludes that until Schanuel's Conjecture is proven or computing power significantly advances, the question of whether pi to the pi to the pi to the pi is an integer remains unanswered.
The video was sponsored by Jane Street, a company offering programs for those interested in careers involving complex problem-solving in finance.
Jane Street sponsors the Stand Up Maths channel, making the production of educational mathematical content possible.
The video was filmed in front of a canned studio audience sample pack, adding a unique element to the production.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: