Calculus 1 - Integration & Antiderivatives

The Organic Chemistry Tutor

10 Jul 201840:03

EducationalLearning

32 Likes 10 Comments

TLDRThis comprehensive video tutorial delves into the process of integration, focusing on the power rule for finding antiderivatives of monomials and polynomials. It explains the concept of indefinite and definite integrals, introduces trigonometric and exponential function integration techniques, and highlights the use of u-substitution for more complex rational functions. The video also emphasizes the importance of the constant of integration and demonstrates the application of the fundamental theorem of calculus in evaluating definite integrals.

Takeaways

📚 The power rule for integration involves adding 1 to the exponent of the variable and dividing by the new exponent, then adding the constant of integration.
🔄 To find the antiderivative of a monomial, apply the adjusted power rule and include the constant of integration in the result.
📈 When dealing with polynomials, integrate each term separately and combine the results with the constant of integration.
🌐 For rational functions, the antiderivative can be found by rewriting the expression and applying the power rule.
🔢 The antiderivative of a constant is the constant times the variable plus the constant of integration.
🌿 The antiderivative of a function involving roots (radical functions) is found by converting the root to a rational exponent, applying the power rule, and simplifying.
📊 Trigonometric functions have specific antiderivative relationships; for example, the antiderivative of cosine X is sine X plus C.
🏛️ The difference between an indefinite integral and a definite integral is that the former gives an expression in terms of X plus C, while the latter provides a numerical value based on the limits of integration.
📐 The fundamental theorem of calculus relates the evaluation of a definite integral to the antiderivative of the function, with the constant of integration canceling out.
📝 For exponential functions with a linear function inside, the antiderivative can be found using the formula e^u divided by the derivative of u, plus C.
🔄 U-substitution is a technique used for integrating more complex functions by replacing a part of the integrand with a new variable (u) and solving for the differential (Du/DX).

Q & A

What is the power rule for derivatives and how does it differ from the power rule for integration?
-The power rule for derivatives states that the derivative of x raised to the nth power is n*x^(n-1). For integration, the power rule is modified by adding 1 to the exponent and dividing by the new exponent, then adding the constant of integration.

Outlines

00:00

📚 Introduction to Integration and the Power Rule

This paragraph introduces the concept of integration and focuses on the power rule for finding antiderivatives. It explains the process of finding the antiderivative of functions, particularly using the power rule. The explanation includes how to manipulate the exponent by adding 1 and dividing by the new exponent, as well as the importance of including the constant of integration. Examples are provided to illustrate the process, such as finding the derivative of x cubed and the antiderivative of 3x squared.

05:06

📈 Working with Constants and Binomials

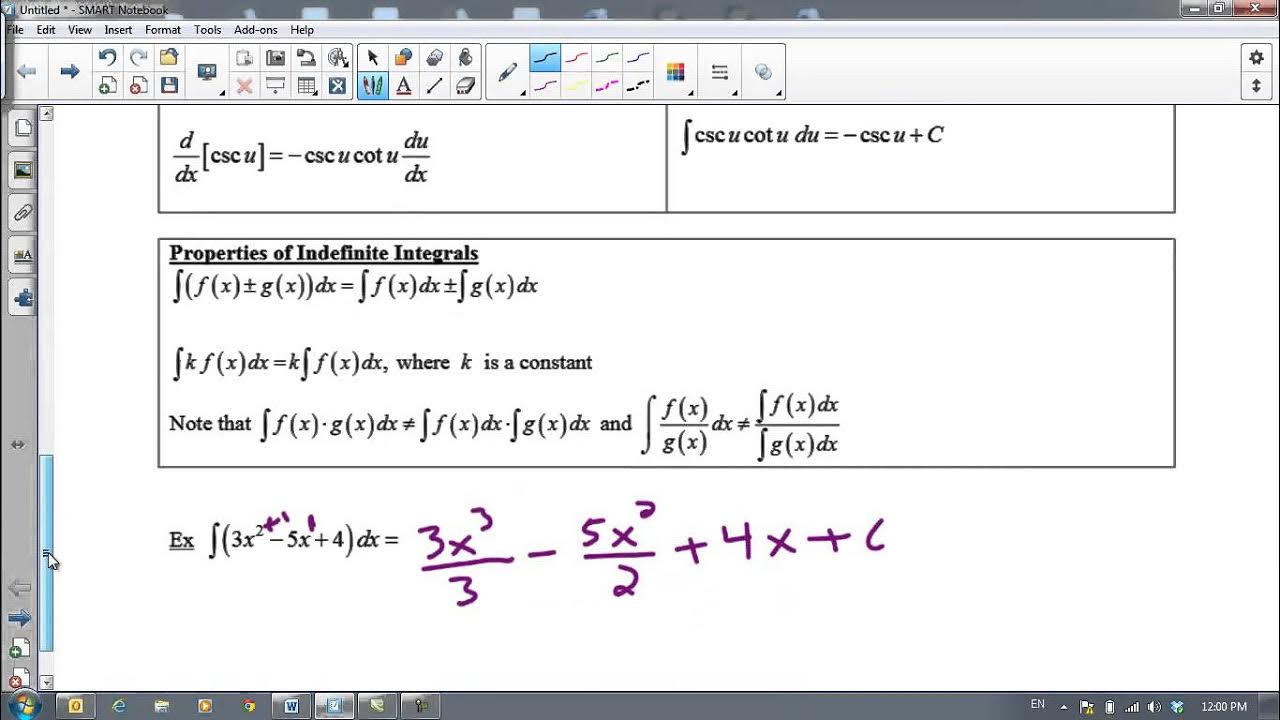
This section delves into integrating constants and binomials. It explains how to handle constants by simply adding a variable to them during integration. The paragraph then moves on to discuss the integration of binomials, like 7x - 6, by integrating each term separately. It emphasizes the need to add the constant of integration after integrating each component. Additional examples are provided, including the integration of trinomials like 6x squared plus 4x minus 7.

10:10

🌟 Radical Functions and Trigonometric Expressions

This part of the script covers the integration of radical functions, such as the square root of x, and trigonometric expressions. It explains the process of rewriting radical expressions with rational exponents and applying the power rule to find their antiderivatives. The paragraph also discusses the integration of trigonometric functions like sine and cosine, and introduces key formulas for these integrations. The explanation includes examples to demonstrate the application of these rules.

15:15

📊 Definite Integrals and the Fundamental Theorem of Calculus

This section introduces the concept of definite integrals and differentiates them from indefinite integrals. It explains that definite integrals provide a numerical value, while indefinite integrals result in an algebraic expression. The fundamental theorem of calculus is briefly mentioned as the basis for evaluating definite integrals. Examples are given to illustrate the process of evaluating both indefinite and definite integrals, emphasizing the disappearance of the constant of integration in definite integrals.

20:17

🧮 Exponential Functions and Integration Techniques

This paragraph focuses on the integration of exponential functions. It presents a formula for integrating exponentials with a linear function and provides examples of its application. The concept of u-substitution is introduced as an alternative technique for integrating more complex exponential functions. The explanation includes a step-by-step demonstration of how to apply u-substitution to find antiderivatives of functions like 4x * e^(x^2).

25:17

📐 Rational Functions and Logarithmic Integration

The final section discusses the integration of rational functions and the antiderivative of 1/x. It explains the process of rewriting rational expressions and using the power rule for integration. The paragraph highlights the use of known formulas, such as the antiderivative of 1/x being ln|x|. It also covers the integration of expressions involving the natural log function and absolute values, providing examples and demonstrating the use of u-substitution for these cases.

Mindmap

Keywords

💡Integration

Integration is a fundamental concept in calculus that involves finding the antiderivative of a given function. It is the reverse process of differentiation and is used to calculate areas under curves, volumes, and other quantities that involve accumulation. In the video, integration is explained through the power rule and various examples, demonstrating how to find the antiderivative of functions like x^n, x^(1/2), and more complex expressions.

💡Power Rule

The power rule is a basic principle in calculus that describes how to differentiate and integrate functions of the form x^n, where n is a constant. For integration, instead of subtracting 1 from the exponent as in differentiation, you add 1 to the exponent and then divide by the new exponent. This rule is essential for integrating monomials and is a key concept explained in the video with several examples.

💡Antiderivative

An antiderivative, also known as an indefinite integral, is a function that represents the reverse process of differentiation. It is used to find the original function from its derivative, by reversing the process of finding rates of change. The antiderivative includes an arbitrary constant, known as the constant of integration, because the derivative of a constant is zero, making it impossible to determine the exact original function without additional information.

💡Constant of Integration

The constant of integration, often denoted as C, is an arbitrary constant added when finding antiderivatives or indefinite integrals. It accounts for the fact that the derivative of a constant is zero, meaning that there are infinitely many functions that could have the same derivative. The constant of integration ensures that the integral of a function is well-defined and represents all possible antiderivatives of that function.

💡Trigonometric Functions

Trigonometric functions, such as sine, cosine, tangent, and their inverses, are periodic functions that relate the angles and sides of a triangle. In the context of the video, these functions are discussed in relation to their derivatives and integrals. The antiderivative of trigonometric functions is essential in solving problems that involve periodic phenomena.

💡Exponential Functions

Exponential functions are mathematical functions of the form a^x, where a is a constant and x is the variable. These functions are important in many areas of mathematics and science, including growth and decay processes. The video discusses how to find the antiderivative of exponential functions, particularly when the exponent is a linear function of x.

💡U-Substitution

U-substitution is a technique used in integration to simplify complex integrands, especially when dealing with rational functions or those involving the derivative of the integrand. It involves replacing the integrand's variable with a new variable (u), solving for the differential (du) in terms of the original variable (dx), and then integrating with respect to u. This method can greatly simplify the process of finding antiderivatives.

💡Rational Functions

Rational functions are mathematical expressions that involve a ratio of two polynomials. They can represent a wide variety of shapes and behaviors, including asymptotes and holes in their graphs. The video discusses techniques for integrating rational functions, such as using u-substitution for certain types of integrands and simplifying the process of finding antiderivatives.

💡Definite Integral

A definite integral represents the signed area under a curve within a specified interval. Unlike the indefinite integral, which provides an antiderivative and includes an arbitrary constant, a definite integral has numerical limits and results in a specific value. The video explains the process of evaluating definite integrals using the fundamental theorem of calculus and the concept of limits of integration.

💡Fundamental Theorem of Calculus

The fundamental theorem of calculus is a key result that connects the processes of differentiation and integration. It states that the definite integral of a function from one point to another is equal to the difference in the values of its antiderivative evaluated at those points. This theorem is crucial for evaluating definite integrals and understanding the relationship between derivatives and integrals.

💡Natural Logarithm

The natural logarithm, denoted as ln(x), is the logarithm to the base e, where e is a mathematical constant approximately equal to 2.71828. It is the inverse function of the exponential function e^x and is used in various applications, including solving for areas under curves and in exponential growth and decay models. The video mentions the natural logarithm in the context of integrating 1/x, where the antiderivative is ln(x) + C.

Highlights

The power rule for derivatives states that the derivative of x raised to the nth power is n*x^(n-1).

For antiderivatives or integration, the power rule involves adding 1 to the exponent and dividing by the new exponent.

The constant of integration is added to the result of the antiderivative calculation.

The antiderivative of x^3 is x^2, and the antiderivative of 3x^2 is (1/3)x^3 + C.

The antiderivative of x^4 is (1/5)x^5 + C, and for x^7 it is (1/8)x^8 + C.

Integration of a monomial involves using the power rule to find the antiderivative.

The antiderivative of a fraction like x/4 involves rewriting the expression and applying the power rule.

The antiderivative of a constant is the constant times the variable plus C.

Integration by parts or u-substitution is used for more complex functions like 7x - 6.

The antiderivative of a binomial like 6x^2 + 4x - 7 involves integrating each term separately.

For radical functions, the power rule is applied after converting the radical to a rational exponent.

The antiderivative of the square root of x (x^(1/2)) is (2/3)x^(3/2) + C.

The antiderivative of trigonometric functions involves using their derivative counterparts, such as the derivative of sin(x) being cos(x).

The difference between an indefinite integral and a definite integral is that the former gives an expression in terms of x, while the latter provides a numerical value.

The fundamental theorem of calculus is used to evaluate definite integrals by substituting the upper and lower limits of integration.

Exponential functions with a linear function inside the exponent can be integrated using the formula e^u/u' + C.

The antiderivative of 1/x is ln|x|, which is a standard result to remember.

U-substitution is a powerful technique for integrating rational functions, such as 1/x^2.

Integration of rational functions often involves rewriting the expression and using techniques like partial fraction decomposition.

The antiderivative of functions involving secant and cosecant involves using their derivative relationships.

The antiderivative of e^(u) where u is a non-linear function can be found using integration by parts or u-substitution.

Transcripts

Browse More Related Video

Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems

Antiderivatives

U-substitution With Definite Integrals

Calculus 2 Final Exam Review -

Integration of Rational Functions By Completing The Square - Calculus

Definite Integral

Related Tags

Power Rule Integration Techniques Exponential Functions Rational Functions Trigonometric Integrals Indefinite Integrals Definite Integrals Calculus Lessons Mathematics Education Online Learning Patreon Content