What is Standard Deviation and Mean Absolute Deviation | Math, Statistics for data science, ML

codebasics
23 Apr 202108:16
EducationalLearning
32 Likes 10 Comments

TLDRThis video introduces the concepts of mean absolute deviation (MAD) and standard deviation, essential in statistics and data science for understanding the spread of data points around the mean. MAD is calculated by taking the mean of the absolute differences between each data point and the mean, while standard deviation involves squaring these differences, averaging them, and then taking the square root. The video uses test scores as an example to illustrate how these metrics can reveal different aspects of data distribution, with standard deviation providing a more nuanced understanding, especially in cases where MAD may not differentiate effectively between data sets with varying ranges.

Takeaways
  • 📈 Mean Absolute Deviation (MAD) is a measure of variability that calculates the average distance of individual data points from the mean.
  • 📊 Standard Deviation is a more advanced measure of data spread that involves squaring the differences, averaging them, and then taking the square root.
  • 📚 The video uses test scores as an example to illustrate the concepts of mean absolute deviation and standard deviation.
  • 🔢 MAD is calculated by taking the mean of the absolute differences between each data point and the mean of the dataset.
  • 📊 Standard Deviation is calculated by taking the square root of the average of the squared differences between each data point and the mean.
  • 🌟 MAD can sometimes be insufficient to represent the spread of data, especially when there are outliers.
  • 📈 The video demonstrates that while MAD might give the same value for two datasets, the actual spread of data points can be different, as shown in the example with one outlier.
  • 🔍 Both MAD and Standard Deviation are important in statistics and data science for understanding the distribution of data.
  • 📊 The concepts of L1 and L2 norms in machine learning relate to MAD and Standard Deviation, respectively.
  • 📱 The video is part of a series and the next installment will likely cover the topic of normal distribution.
  • 👍 The video aims to provide a basic understanding of standard deviation and mean absolute deviation for those learning statistics or data science.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is to explain the concepts of mean absolute deviation and standard deviation in the context of data analysis.

  • What are the two key metrics introduced in the video for understanding data spread?

    -The two key metrics introduced are Mean Absolute Deviation (MAD) and Standard Deviation (σ).

  • How is the average score of the history test calculated in the example?

    -The average score is calculated by adding all the individual test scores and dividing by the number of scores.

  • What does the video illustrate about the data points in the history test versus the mathematics test?

    -The video illustrates that while the average score is the same for both tests, the data points in the mathematics test are more spread out from the average compared to the history test.

  • What is the formula for calculating Mean Absolute Deviation (MAD)?

    -MAD is calculated by taking the absolute differences between each data point and the mean, then taking the average of these differences.

  • Why might Mean Absolute Deviation (MAD) not be sufficient in some scenarios?

    -MAD might not be sufficient when there is a significant outlier in the data set, as it does not account for the magnitude of deviation from the mean.

  • How is Standard Deviation (σ) calculated?

    -Standard Deviation is calculated by taking the square of the differences between each data point and the mean, averaging those squares, and then taking the square root of that average.

  • What is the significance of the square root operation in the calculation of Standard Deviation?

    -The square root operation is used to revert the data to its original scale after squaring the differences, which helps in interpreting the standard deviation in the same units as the original data.

  • How does the video relate the concepts of L1 and L2 norms to Mean Absolute Deviation and Standard Deviation?

    -The video mentions that L1 norm refers to Mean Absolute Deviation, while L2 norm refers to Standard Deviation, which are used in machine learning techniques such as ridge regression and lasso regression.

  • What is the practical application of understanding Standard Deviation and Mean Absolute Deviation in data science?

    -Understanding these concepts is crucial for data analysis and interpretation, as they provide insights into the spread and variability of data points, which is essential for making informed decisions and predictions in data science and statistics.

  • Why is it important to have a single metric to represent data spread when dealing with large data sets?

    -A single metric to represent data spread is important for large data sets because it simplifies the analysis, allowing for quick and meaningful comparisons between different data sets and for identifying patterns or anomalies more efficiently.

Outlines
00:00
📊 Introduction to Absolute Deviation and Standard Deviation

This paragraph introduces the concepts of absolute deviation and standard deviation using the context of test scores. It explains how to calculate the mean absolute deviation by finding the average of the differences between individual scores and the mean score. The example given compares the spread of scores in a history test versus a mathematics test, highlighting the usefulness of these metrics in understanding data distribution. The paragraph also touches on the limitations of mean absolute deviation in certain scenarios, setting the stage for the introduction of standard deviation in the next paragraph.

05:02
📈 Calculation and Application of Standard Deviation

The second paragraph delves into the calculation and application of standard deviation as a more accurate measure of data spread. It describes the process of squaring the differences between individual data points and the mean, averaging these squares, and then taking the square root of the average. This method is compared to mean absolute deviation, showing how standard deviation can better represent the spread of data, especially when outliers are present. The paragraph also connects the concepts to machine learning terms like L1 and L2 norms, and mentions their relevance in future discussions on normal distribution.

Mindmap
Keywords
💡Mean Absolute Deviation (MAD)
Mean Absolute Deviation (MAD) is a measure of variability that calculates the average distance of individual data points from the mean. It is defined as the average of the absolute differences between each data point and the mean. In the video, MAD is used to compare the spread of scores in two different tests, showing that a higher MAD indicates a greater spread of data points from the average, as seen in the mathematics test scores with a MAD of 23 compared to the history test scores with a MAD of 3.16.
💡Standard Deviation (σ)
Standard Deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of values. It is calculated by taking the square root of the average of the squared differences from the mean. Standard deviation provides a more accurate representation of data spread, especially when there are outliers. In the video, the standard deviation is introduced as a more informative measure than MAD when dealing with data sets that have outliers or are not symmetrically distributed around the mean.
💡Data Points
Data points refer to individual values or observations within a data set. They are usually represented as coordinates on a graph or chart. In the context of the video, data points are used to represent test scores, and their relationship to the mean score is analyzed to understand the spread and variability of the scores.
💡Average (Mean)
The average, or mean, is a central tendency measure that represents the typical value of a data set by dividing the sum of all the data points by the number of points. It provides an idea of the central or 'typical' score in a set of test scores. The video uses the average to establish a baseline against which the deviation of individual scores can be measured.
💡Spread
Spread refers to the degree of dispersion or distribution of data points around a central value, such as the mean. A larger spread indicates that the data points are more varied and farther from the central value. In the video, understanding the spread of data points is crucial for determining the variability and consistency of test scores.
💡Histogram
A histogram is a graphical representation of the distribution of a data set, where individual data points are grouped into intervals (or bins) and displayed as bars. Although not explicitly mentioned in the video, the concept of a histogram is implied when discussing how data points would appear when plotted on a chart, with the average represented by a yellow line.
💡Outliers
Outliers are data points that are significantly different from the other values in a data set. They can have a substantial impact on the analysis of the data, especially in measures of dispersion like standard deviation. The video suggests that standard deviation is a better measure than MAD when dealing with outliers, as it accounts for the magnitude of the deviation.
💡Statistics
Statistics is a branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. It is the science of understanding data through the use of various methods, including the calculation of measures like mean, median, mode, standard deviation, and mean absolute deviation. The video is centered around teaching basic statistical concepts such as mean absolute deviation and standard deviation.
💡Data Science
Data Science is an interdisciplinary field that uses scientific methods, processes, algorithms, and systems to extract knowledge and insights from structured and unstructured data. It involves techniques and principles from disciplines like statistics, machine learning, and information science. The video mentions data science as a field where understanding concepts like mean absolute deviation and standard deviation is crucial.
💡Machine Learning
Machine Learning is a subset of artificial intelligence that provides systems the ability to learn from and make decisions based on data. It involves the development of algorithms that allow computers to learn from and make predictions or decisions without explicit programming. The video briefly touches on machine learning concepts such as L1 and L2 norms, which are related to mean absolute deviation and standard deviation.
Highlights

Mean absolute deviation and standard deviation are key concepts in statistics and data science.

Mean absolute deviation (MAD) measures how far individual data points are from the average.

Standard deviation quantifies the spread of data points with respect to the mean.

The video uses test scores as an example to illustrate the concepts of mean absolute deviation and standard deviation.

MAD is calculated by taking the mean of the absolute differences between each data point and the mean.

Standard deviation is calculated by taking the square root of the average of the squared differences between each data point and the mean.

MAD can sometimes be insufficient to accurately represent data distribution, as shown in the example with a single outlier.

The video demonstrates that while MAD shows the same value for two datasets, their data distribution can be quite different.

L1 and L2 norms in machine learning are related to mean absolute deviation and standard deviation, respectively.

Understanding standard deviation and mean absolute deviation is fundamental for anyone learning statistics or data science.

The video provides a clear and simple explanation of the concepts using a relatable example.

The process of calculating mean absolute deviation and standard deviation is broken down step by step in the video.

The video emphasizes the practical applications of these concepts in fields like data science and machine learning.

The video is designed to be a quick and informative guide to understanding mean absolute deviation and standard deviation.

The video encourages viewers to pause and think about the concepts before revealing the calculations.

The video concludes with a teaser for the next topic, which will likely be on normal distribution.

The video is part of a series that aims to provide a basic understanding of essential statistical concepts.

Transcripts

Browse More Related Video

Standard Deviation & Mean Absolute Deviation Explained - 6-8-19]

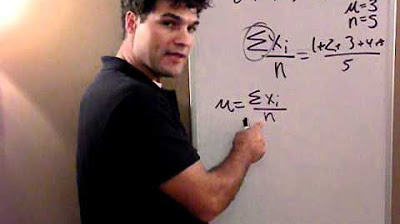
What is a "Standard Deviation?" and where does that formula come from

How to Calculate Standard Deviation

Find the Mean, Variance, & Standard Deviation of Frequency Grouped Data Table| Step-by-Step Tutorial

MEAN, VARIANCE, AND STANDARD DEVIATION FOR UNGROUPED DATA

Mean Absolute Deviation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Data AnalysisStatistical ConceptsMean Absolute DeviationStandard DeviationData SpreadMathematicsData ScienceEducational VideoMachine LearningStatistical Metrics