Statistical Inference Definition with Example | Statistics Tutorial #18 | MarinStatsLectures

MarinStatsLectures-R Programming & Statistics
30 Aug 201805:29
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides a foundational understanding of statistical inference, focusing on the concept of a single mean. It introduces the sampling distribution, standard error, and how they relate to confidence intervals and hypothesis testing. The importance of p-values in determining the probability of obtaining an estimate or a more extreme one under a null hypothesis is emphasized. The script touches on both parametric and nonparametric approaches, highlighting that while methods may vary, the core concepts remain consistent. The goal is to build a strong basis for understanding more advanced statistical methods without relying on hand calculations.

Takeaways
  • 🏗️ Foundation of statistical inference was laid, focusing on a single mean.
  • 📊 The sampling distribution was discussed as the theoretical set of all possible estimates.
  • 🔍 The standard error measures the average distance an estimate moves from the population value.
  • ✅ Confidence intervals were introduced as a way to estimate the population mean with a margin of error.
  • 💡 Hypothesis testing and p-values were explained to determine if a population mean differs significantly from a hypothesized value.
  • 📈 The concepts of confidence intervals and hypothesis testing apply to various types of estimates.
  • 🔢 The general form of a confidence interval is the estimate plus or minus some margin of error.
  • 🅿️ Test statistics in hypothesis testing compare the sample estimate to the hypothesized value, scaled by the standard error.
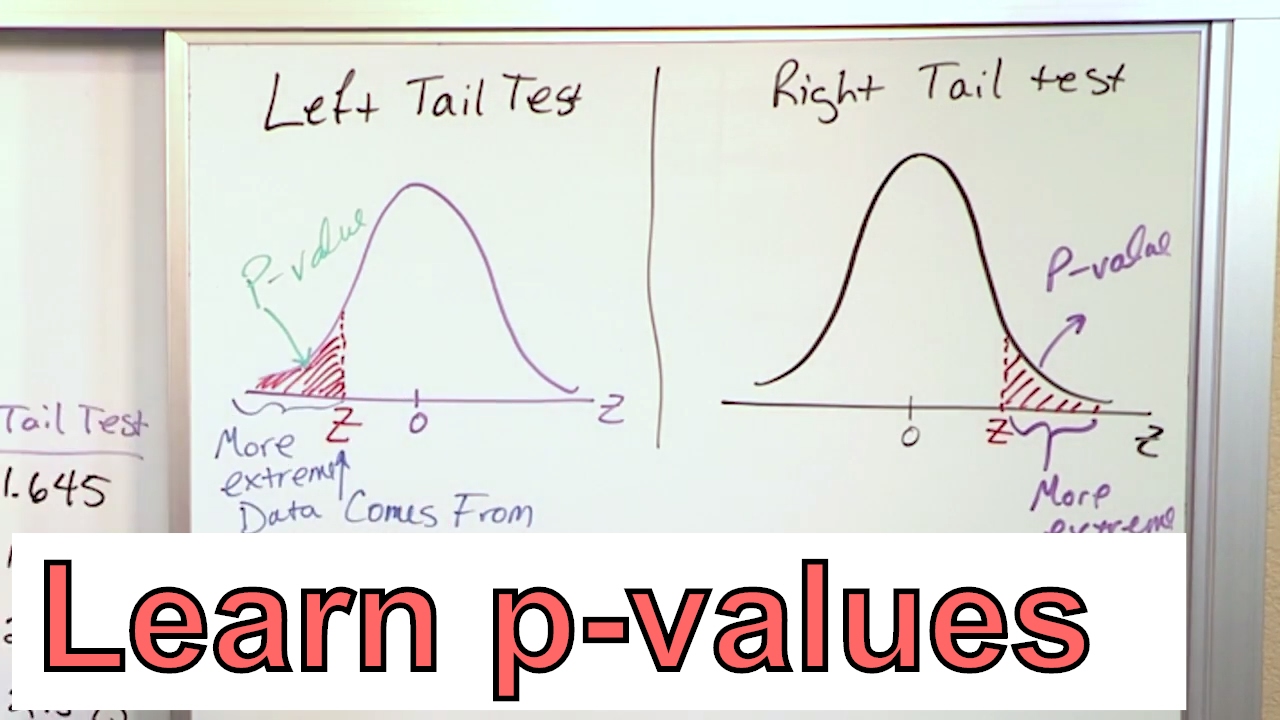
  • 🎯 P-value calculation provides the probability of obtaining an estimate as extreme as, or more extreme than, the observed if the null hypothesis is true.
  • 🧪 Parametric and nonparametric tests were mentioned, highlighting that the underlying concepts remain consistent across different approaches.
  • 📚 Future learning will focus more on understanding the calculations and software applications rather than hand calculations.
Q & A

  • What is the main focus of the statistical inference foundation discussed in the transcript?

    -The main focus is on understanding the concepts related to a single mean, including the sampling distribution, standard error, confidence intervals, and hypothesis testing with p-values.

  • How does the sampling distribution relate to the estimate of a mean?

    -The sampling distribution describes the theoretical set of all possible estimates of the mean, considering the estimate as one of many that could be obtained from different samples.

  • What is the role of the standard error in statistical inference?

    -The standard error provides an idea of how far an estimate will, on average, move from the true or population value, which is crucial for constructing confidence intervals.

  • How does a confidence interval help in statistical analysis?

    -A confidence interval gives a range estimate plus or minus a margin of error, allowing us to be confident that the interval captures the true population mean.

  • What is the purpose of hypothesis testing in statistics?

    -Hypothesis testing is used to determine if the mean in the population is significantly larger, smaller, or different from a hypothesized value.

  • How is a p-value calculated and what does it represent?

    -A p-value is calculated by comparing the observed estimate to what would be expected under a null hypothesis, and it represents the probability of obtaining an estimate as extreme or more extreme if the null hypothesis is true.

  • What is the difference between parametric and nonparametric tests?

    -Parametric tests assume that the data follows a specific distribution (like the normal distribution), while nonparametric tests do not make such assumptions and are often used with small sample sizes or non-normal distributions.

  • How does the bootstrap approach differ from traditional statistical methods?

    -The bootstrap approach involves resampling the data with replacement to create many pseudo-samples, from which statistics can be calculated, providing estimates without relying on distributional assumptions.

  • Why is it important to understand the underlying concepts in statistical methods, even when using software?

    -Understanding the underlying concepts helps in interpreting the results correctly, knowing the assumptions behind the methods, and applying them appropriately to the data at hand.

  • What can change when applying statistical methods to different types of estimates?

    -The mathematical details and specific formulas may change, but the foundational concepts of confidence intervals, hypothesis testing, and the interpretation of p-values remain the same.

  • How does the transcript suggest approaching more advanced statistical methods in future learning?

    -The transcript suggests that future learning will rely more on software for calculations, and while the formulas will be studied for understanding, hand calculations will not be the focus as they have been up to this point.

Outlines
00:00
📊 Foundation of Statistical Inference

This paragraph discusses the foundational concepts of statistical inference, focusing on the estimation of a single mean. It introduces the sampling distribution, which represents the theoretical set of all possible estimates, and the standard error, which measures the average deviation of an estimate from the true population value. The paragraph explains how these concepts are used to construct confidence intervals and perform hypothesis testing. It emphasizes the importance of understanding the underlying principles, regardless of the type of estimate or the mathematical details involved. The discussion also touches on the use of p-values to determine the probability of obtaining an estimate as extreme as the one observed, or more extreme, if the null hypothesis is true.

05:00
🎓 Understanding Advanced Statistical Approaches

The second paragraph shifts the focus to the understanding of more advanced statistical approaches. It highlights the importance of grasping the foundational concepts to better comprehend the formulas and calculations used in software for various analytical methods. The paragraph mentions different types of tests, such as the one-sample t-test, and approaches like bootstrapping and nonparametric methods. It reassures that the core concepts of confidence intervals and hypothesis testing remain consistent across these different analytical techniques. The speaker also encourages viewers to stay tuned for more statistics content, promising a fun learning experience.

Mindmap
Keywords
💡Statistical Inference
Statistical inference is the process of drawing conclusions about a population using data from a sample. In the video, it is the central theme around which concepts like confidence intervals, hypothesis testing, and p-values revolve. The speaker emphasizes the importance of understanding these tools to make informed decisions based on data analysis.
💡Sampling Distribution
The sampling distribution is a theoretical distribution of possible sample statistics, such as the sample mean, based on an infinite number of random samples of the same size from the same population. In the context of the video, it is used to describe the variability of sample means and is crucial for understanding confidence intervals and hypothesis testing.
💡Standard Error
The standard error is a measure of the variability of a sample statistic, such as the sample mean, in relation to the population parameter it estimates. It provides an idea of how much the sample statistic is expected to deviate from the true population value. In the video, the standard error is used to discuss the precision of the mean as an estimate and to calculate confidence intervals.
💡Confidence Intervals
A confidence interval is a range of values, derived from a statistical model, that is likely to contain the value of an unknown parameter. It provides a level of confidence, usually expressed as a percentage, that the interval captures the true population parameter. In the video, confidence intervals are used to express the precision of the mean estimate.
💡Hypothesis Testing
Hypothesis testing is a statistical method used to make decisions about a population parameter based on a sample. It involves formulating a null hypothesis, calculating a test statistic, and determining a p-value to assess whether the null hypothesis can be rejected. The video introduces hypothesis testing as a foundational concept for statistical inference.
💡P-Values
A p-value, or probability value, is the probability of obtaining a test statistic as extreme or more extreme than the one observed, given that the null hypothesis is true. It is used in hypothesis testing to determine the strength of evidence against the null hypothesis. In the video, p-values are introduced as a way to quantify the evidence against a hypothesized value.
💡Parametric Tests
Parametric tests are statistical tests that assume the data follows a specific distribution, typically a normal distribution. These tests are based on parameters of the distribution and are used when the data meets certain assumptions, such as normality and equal variances. In the video, parametric tests like the one-sample t-test are mentioned as part of the foundational knowledge for statistical inference.
💡Bootstrap Approaches
Bootstrap approaches are a class of statistical methods that involve resampling from the original data set with replacement to create many pseudo-samples. These methods are used to estimate the sampling distribution of a statistic without assuming a specific distribution for the population. In the video, bootstrap approaches are mentioned as an alternative to parametric tests.
💡Estimate
In statistics, an estimate is a value derived from a sample that is used to infer a characteristic of the population from which the sample was taken. Estimates can be for various parameters such as the mean, difference in means, or correlation. The video emphasizes the concept of estimates and their relationship with confidence intervals and hypothesis testing.
💡Margin of Error
The margin of error is the difference between the observed value of a statistic and the true value of the parameter it estimates. It is used in constructing confidence intervals and is a measure of the precision of an estimate. In the video, the margin of error is added to and subtracted from the estimate to form a confidence interval.
💡Null Hypothesis
The null hypothesis is a statistical hypothesis that there is no significant difference or effect between groups or variables. It is the default assumption in hypothesis testing and must be rejected or failed to be rejected based on the evidence provided by the data. In the video, the null hypothesis is discussed as the basis for calculating p-values and conducting hypothesis tests.
Highlights

Laying the foundation for statistical inference with a focus on a single mean.

Discussion on the sampling distribution and its role in describing the theoretical set of all possible estimates.

Explanation of the standard error as a measure of how far an estimate moves from the true population value on average.

Utilization of confidence intervals to estimate and add a margin of error to capture the true population mean.

Introduction to hypothesis testing and the concept of p-values.

Understanding how to test if the population mean is significantly different from a hypothesized value.

The general idea of a confidence interval as an estimate plus or minus a margin of error.

Adapting the concept of confidence intervals to different types of estimates such as differences in means or correlation.

The underlying concepts of confidence intervals and hypothesis testing remaining constant despite changes in mathematical details.

Calculation of test statistics for hypothesis testing by comparing sample estimates to hypothesized values.

The role of p-values in determining the probability of obtaining the estimate or one more extreme if the null hypothesis is true.

Discussion of parametric tests like the one-sample t-test and confidence intervals.

Mention of nonparametric approaches like bootstrap and resampling methods.

Emphasis on the consistency of underlying concepts across different statistical methods, whether parametric or nonparametric.

The transition from hand calculations to relying more on software for advanced analytical approaches.

The importance of understanding the formulas and calculations for grasping the underlying concepts of statistical methods.

A summary of the foundational concepts for confidence intervals, hypothesis testing, and statistical inference.

Transcripts

Browse More Related Video

Meaning of P-value and Alpha

Hypothesis Test vs. Confidence Interval | Statistics Tutorial #15 | MarinStatsLectures

Central Limit Theorem & Sampling Distribution Concepts | Statistics Tutorial | MarinStatsLectures

Statistics Course Overview | Best Statistics Course | MarinStatsLectures

Elementary Stats Lesson #20

Calculate the P-Value in Statistics - Formula to Find the P-Value in Hypothesis Testing

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticalInferenceConfidenceIntervalsHypothesisTestingSamplingDistributionStandardErrorEstimateVariabilityTValueDataAnalysisParametricTestsNonparametricApproaches