Limit of (1-cos(x))/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
TLDRIn the video, the instructor demonstrates how to calculate the limit of (1 - cos(x))/x as x approaches zero. By leveraging the known limit of (sin(x))/x as x approaches zero, equal to one, and using algebraic manipulation along with trigonometric identities, the instructor simplifies the expression and shows that the limit equals zero. The explanation is clear, methodical, and encourages users to verify the result graphically.
Takeaways
- 📚 The main goal of the video is to find the limit of (1 - cos(x))/x as x approaches zero.
- 🧠 The video assumes prior knowledge of the limit of (sin(x))/x as x approaches zero, which is equal to one.
- 🎓 A key step in solving the problem is algebraically manipulating the expression by multiplying the numerator and denominator by (1 + cos(x)).
- 🔢 After manipulation, the expression can be rewritten as (1 - cos^2(x))/(x(1 + cos(x))) which simplifies to (sin^2(x))/(x(1 + cos(x))) using the Pythagorean identity.
- 📈 The video demonstrates the use of the squeeze theorem, although not explicitly mentioned, by leveraging known limits and trigonometric identities.
- 🤝 The concept of limits of products is introduced, stating that the limit of the product of two expressions is equal to the product of their individual limits.
- 📊 The video encourages viewers to confirm the result graphically by graphing the function.
- 🥇 The final result of the limit (1 - cos(x))/x as x approaches zero is found to be zero.
- 🌟 The video highlights the importance of understanding and applying algebraic manipulation and trigonometric identities in calculus.
- 🔍 The process of solving the limit involves breaking down complex expressions into simpler forms that can be evaluated more easily.
- 🎯 The video serves as an example of how to tackle limits in calculus by combining mathematical techniques and theorems.
Q & A
What is the main topic of the video?
-The main topic of the video is to find the limit of the expression (1 - cos(x)) / x as x approaches zero.
What assumption is made at the beginning of the video?
-The assumption made at the beginning of the video is that the limit of (sin(x)) / x as x approaches zero is equal to one.
How does the instructor manipulate the given expression algebraically?
-The instructor multiplies both the numerator and the denominator of the expression by (1 + cos(x)) to simplify it.
What trigonometric identity is used in the solution?
-The Pythagorean identity, which states that sin^2(x) + cos^2(x) = 1, is used to rewrite 1 - cos^2(x) as sin^2(x).
What property of limits is used to simplify the expression further?
-The property that the limit of a product of two expressions is the product of their individual limits is used to simplify the expression.
What is the value of the limit (sin(x)) / (1 + cos(x)) as x approaches zero?
-As x approaches zero, the value of (sin(x)) / (1 + cos(x)) approaches zero, since sin(0) is zero and (1 + cos(0)) is 2.
What is the final result of the limit (1 - cos(x)) / x as x approaches zero?
-The final result of the limit (1 - cos(x)) / x as x approaches zero is zero.
How does the instructor suggest verifying the result?
-The instructor suggests graphing the function to visually confirm that the limit makes sense and corresponds to the calculated value.
Why is the assumption about the limit of (sin(x)) / x important?
-The assumption is important because it allows the instructor to leverage a previously proven result to solve the new limit problem without having to re-prove the foundational limit.
What is the significance of the difference of squares in the solution?
-The difference of squares is significant because it simplifies the expression and allows the trigonometric identity to be applied, leading to the solution of the limit.
How does the video demonstrate the use of algebraic manipulation in solving limits?
-The video demonstrates the use of algebraic manipulation by showing how multiplying by a form of one (1 + cos(x)) can transform the original expression into a more manageable form that can be solved using known trigonometric identities and limit properties.
Outlines
📚 Mathematical Analysis - Limit of (1 - cos(x)) / x as x approaches 0
In this video segment, the instructor aims to calculate the limit of (1 - cos(x)) / x as x approaches zero. It is assumed that the viewer is already familiar with the limit of sine of x over x as x approaches zero, which is equal to one. The instructor begins by algebraically manipulating the given expression by multiplying both the numerator and the denominator by one plus the cosine of x. This leads to the rewriting of the expression in terms of the Pythagorean trigonometric identity, which allows the transformation of the limit into a more recognizable form. The instructor then uses the known limit of sine of x over x, which is one, and applies it to the transformed expression to find the limit of the original function. The result of the limit is found to be zero, which is also supported by a graphical interpretation that encourages viewers to verify the result by graphing the function.
Mindmap
Keywords
💡limit
💡cosine
💡sine
💡algebraic manipulation
💡Pythagorean identity
💡squeeze theorem
💡denominator
💡numerator
💡asymptote
💡trigonometric identities
💡product of limits
Highlights
The video aims to find the limit of (1 - cos(x))/x as x approaches 0.
A pre-known fact used in the video is that the limit of (sin(x))/x as x approaches 0 is equal to 1.
The proof of the famous limit (sin(x))/x -> 1 as x -> 0 is demonstrated using the squeeze theorem in another video.
The expression is algebraically manipulated by multiplying the numerator and denominator by (1 + cos(x)).
The rewritten expression after manipulation is (1 - cos(x) * (1 + cos(x)))/(x * (1 + cos(x))).
The expression simplifies to (1 - cos^2(x))/(x * (1 + cos(x))) using the difference of squares.
According to the Pythagorean trig identity, 1 - cos^2(x) is equivalent to sin^2(x).
The limit can be expressed as the product of two limits: (sin(x))/x * (sin(x))/(1 + cos(x)) as x approaches 0.
The first limit, (sin(x))/x as x approaches 0, is known to be equal to 1.
The second limit, (sin(x))/(1 + cos(x)) as x approaches 0, is straightforward to evaluate.
As x approaches 0, sin(x) approaches 0 and cos(x) approaches 1, making the denominator of the second limit approach 2.
The product of the limits results in 0, since the numerator of the second limit approaches 0 while the denominator approaches 2.
The final result of the original limit is 0, demonstrated through trigonometric identities and algebraic manipulation.
The video encourages viewers to graph the function to visually confirm the result makes sense.
The video effectively uses algebraic techniques and trigonometric identities to simplify and solve the limit problem.
Transcripts
Browse More Related Video

Zero-Bounded Limit Theorem (with example)

Limits of Trigonometric Functions
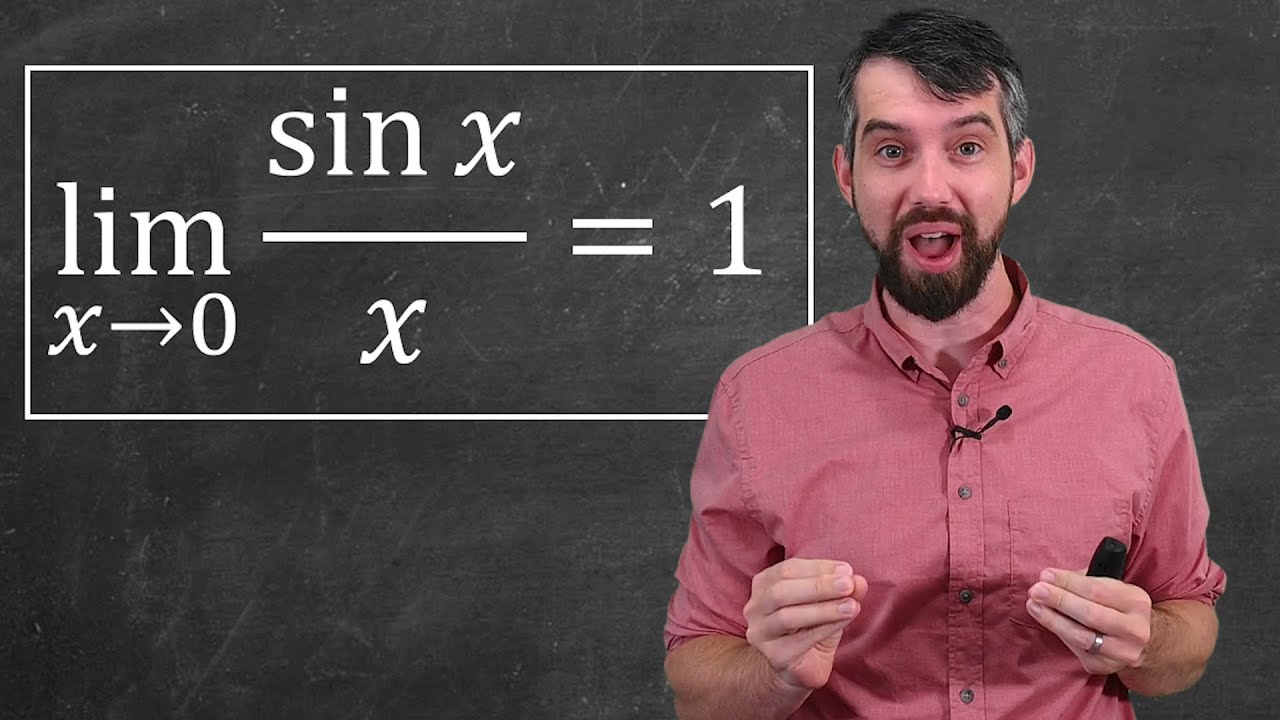
The most important limit in Calculus // Geometric Proof & Applications

Example (2.2) - Finding the limit of a function #10 (Calc)

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

Trig limit using pythagorean identity | Limits and continuity | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: