Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (91 of 92) Modeling Polonium-212 Decay

Michel van Biezen
20 May 201807:05
EducationalLearning
32 Likes 10 Comments

TLDRIn this online lecture, the focus is on modeling the decay of a highly radioactive element, Polonium 212, using the concept of barrier penetration. The lecture explores the probability of an alpha particle escaping the nucleus by overcoming a potential barrier, initially assuming a square barrier model. The calculated probability is extremely low, leading to a discrepancy when compared to the observed half-life of Polonium 212. The explanation for this difference lies in the assumption of a square barrier, which is not accurate as real barriers decrease exponentially. The lecture concludes with a teaser for the next video, where a more precise method of calculating the decay probability by dividing the barrier into small sections will be discussed.

Takeaways
  • 🌟 Polonium-212 is highly radioactive with an extremely short half-life of 0.3 microseconds.
  • 🚀 The lecture focuses on modeling the escape of an alpha particle from the nucleus of Polonium-212 through a potential barrier.
  • 📈 The potential barrier's peak is 26.4 MeV s, and the alpha particle's energy is 8.78 MeV, creating a difference of 17.62 MeV.
  • 🧮 The probability of an alpha particle penetrating the potential barrier is calculated using the transmission coefficient.
  • 🎢 Initially, the potential barrier is modeled as a square barrier for simplicity.
  • 🔧 The Alpha value is calculated as 1.84 × 10^15, which is used to find the transmission coefficient.
  • 📉 The calculated transmission probability is extremely low, at 2.47 × 10^-29.
  • 🔴 The actual attempt frequency of an alpha particle trying to escape is 1.1 × 10^21 times per second.
  • 🕰️ The calculated half-life based on the transmission probability is significantly longer than the observed half-life of Polonium-212.
  • 🧬 The discrepancy is due to the assumption of a square barrier; real barriers decrease more quickly, affecting the Alpha value.
  • 🔄 The next step involves dividing the barrier into small sections and calculating the probability of passage through each to get a more accurate half-life.
Q & A

  • What is the half-life of Polonium 212?

    -The half-life of Polonium 212 is 0.3 microseconds, making it a very unstable and highly radioactive element.

  • What is the significance of the half-life of an element?

    -The half-life of an element is the time it takes for half of the radioactive particles of that element to decay. It's a key parameter in understanding the stability and decay rate of radioactive materials.

  • What is an alpha particle in the context of radioactivity?

    -An alpha particle is a type of particle that consists of two protons and two neutrons, which is emitted during the radioactive decay of certain elements like Polonium 212.

  • What is a potential barrier in nuclear physics?

    -A potential barrier in nuclear physics represents the energy barrier that a particle, such as an alpha particle, must overcome to escape the nucleus during radioactive decay.

  • What is the peak magnitude of the potential barrier for an alpha particle of Polonium 212?

    -The peak magnitude of the potential barrier for an alpha particle of Polonium 212 is 26.4 MeV s.

  • How does the energy of the alpha particle compare to the potential barrier's peak magnitude?

    -The energy of the alpha particle is 8.78 MeV, which is significantly lower than the potential barrier's peak magnitude of 26.4 MeV s, indicating a large difference that affects the probability of decay.

  • What is the calculated transmission coefficient (probability) of an alpha particle breaking through the potential barrier?

    -The calculated transmission coefficient, or the probability of an alpha particle breaking through the potential barrier, is approximately 2.47 x 10^-29.

  • How often does an alpha particle attempt to break through the barrier in Polonium 212?

    -An alpha particle in Polonium 212 attempts to break through the barrier approximately 1.1 x 10^21 times per second.

  • What is the calculated number of alpha particles per second that will break through the barrier?

    -The calculated number of alpha particles per second that will break through the barrier is approximately 2.7 x 10^-8.

  • What is the estimated half-life based on the calculated probability and frequency of decay?

    -The estimated half-life based on the calculated probability and frequency of decay is about 1.5 x 10^6 seconds, which is significantly longer than the observed half-life of 0.3 microseconds.

  • Why is there a discrepancy between the observed half-life and the calculated half-life?

    -The discrepancy is due to the assumption of a square barrier in the initial calculation. In reality, the potential barrier drops off exponentially, which affects the alpha value and the transmission coefficient, leading to a different half-life calculation.

  • How can the model be improved to more accurately predict the half-life of Polonium 212?

    -The model can be improved by dividing the barrier into small sections and calculating the probability of making it through each section, then multiplying all those probabilities together to get a more accurate estimate of the half-life.

Outlines
00:00
📚 Quantum Tunneling of Polonium 212

This paragraph discusses the quantum tunneling effect of an alpha particle escaping from a Polonium 212 nucleus. It explains the concept of barrier penetration with a focus on the radioactive element Polonium 212, which has a very short half-life of 0.3 microseconds. The lecture attempts to model the alpha particle's escape through a potential barrier, calculating the transmission coefficient (probability) of the particle making it through. Initially, the barrier is modeled as a square barrier with a peak magnitude of 26.4 MeV s, and the alpha particle's energy is 8.78 MeV. The calculation involves the use of the Alpha value, which is derived from the mass of the alpha particle, the energy difference, and Planck's constant (h-bar). The result is a very low probability of 2.47 x 10^-29 for the alpha particle to tunnel through the barrier. However, considering the unstable nature of the nucleus, the particle attempts to break through 1.1 x 10^21 times per second, leading to an actual observed half-life much shorter than the calculated one. The discrepancy is attributed to the simplified square barrier model used in the calculation.

05:00
🔬 Refining the Quantum Tunneling Model

The second paragraph addresses the discrepancy between the calculated half-life of Polonium 212 using a square barrier model and the observed half-life. It is noted that the actual potential barrier is not square but decreases exponentially, which affects the Alpha value and the transmission coefficient. To refine the model, the barrier is divided into small sections, and the probability of tunneling through each section is calculated and multiplied together. This refined approach aims to provide a more accurate estimate of the half-life of the alpha particle escaping from Polonium 212. The paragraph concludes with a teaser for the next video, where the refined model will be implemented and explained in detail.

Mindmap
Keywords
💡Polonium 212
Polonium 212 is a radioactive isotope with an extremely short half-life of 0.3 microseconds, making it highly unstable and very radioactive. In the video, it is used as an example to illustrate the process of alpha particle emission and the calculation of decay rates. The video discusses the attempt of an alpha particle to leave the nucleus of polonium 212 and the energy difference it must overcome.
💡Half-life
Half-life is the time required for half of the radioactive nuclei in a sample to decay. It is a fundamental concept in nuclear physics and is used to describe the stability of radioactive elements. In the context of the video, the calculated half-life for polonium 212 is compared with the observed half-life to highlight the discrepancy caused by the simplification of the potential barrier model.
💡Barrier Penetration
Barrier penetration refers to the process by which a particle tunnels through a potential barrier that it classically could not overcome due to insufficient energy. In nuclear physics, this concept is crucial for understanding alpha decay, where an alpha particle must penetrate the potential barrier of the nucleus to escape. The video uses the example of polonium 212 to model and calculate the probability of barrier penetration by an alpha particle.
💡Alpha Particle
An alpha particle is a helium nucleus composed of two protons and two neutrons. It is emitted during the radioactive decay process of certain elements, such as polonium 212. Alpha particles have a +2 charge and a mass approximately four times that of a proton. In the video, the alpha particle's attempt to escape the nucleus of polonium 212 is central to the discussion of barrier penetration and decay rates.
💡Potential Barrier
In the context of nuclear physics, a potential barrier represents the energy barrier that a particle must overcome to escape the nucleus during radioactive decay. The video discusses the concept of a potential barrier and its role in alpha decay, using the example of polonium 212 to illustrate the calculation of the probability of a particle overcoming this barrier.
💡Transmission Coefficient
The transmission coefficient is a measure of the probability that a particle will penetrate a potential barrier. It is used in quantum mechanics to describe tunneling phenomena, such as alpha decay. In the video, the transmission coefficient is calculated to determine the likelihood of an alpha particle escaping the nucleus of polonium 212.
💡Quantum Tunneling
Quantum tunneling is a quantum mechanical phenomenon where a particle can pass through a potential barrier that it classically could not overcome. This concept is essential for understanding the decay of radioactive nuclei, such as polonium 212, where particles can escape despite the presence of a potential barrier.
💡Energy Difference
The energy difference refers to the disparity in energy levels between two states. In the context of the video, it is the difference between the alpha particle's energy and the peak of the potential barrier. This difference is crucial for calculating the probability of barrier penetration and the decay rate of radioactive elements.
💡Femtometer
A femtometer (fm) is a unit of length in the metric system, equivalent to one quadrillionth of a meter (10^-15 meters). It is commonly used in nuclear physics to describe the scale of atomic and subatomic structures. In the video, the distance of the potential barrier is given in femtometers to provide a sense of the scale at which nuclear processes occur.
💡Frequency
In the context of the video, frequency refers to the number of times a radioactive nucleus attempts to decay per unit of time. It is used to calculate the number of alpha particles that will successfully decay from a sample of polonium 212 each second.
💡Decay Rate
The decay rate is the speed at which a radioactive substance decays over time. It is determined by the half-life of the substance and is used to predict how much of a radioactive material will remain after a certain period. In the video, the decay rate is discussed in relation to the calculated half-life of polonium 212 and the observed half-life.
Highlights

The lecture focuses on modeling the barrier penetration of a radioactive element, specifically Polonium 212.

Polonium 212 has an extremely short half-life of 0.3 microseconds, making it highly radioactive.

The alpha particle from Polonium 212 must overcome a potential barrier with a peak magnitude of 26.4 MeV s.

The alpha particle's energy is 8.78 MeV, resulting in a difference of 17.62 MeV.

The potential barrier is not a square barrier in reality but drops off exponentially.

The distance of the barrier is approximately 17.9 femtometers.

The transmission coefficient, or the probability of the particle making it through the barrier, is calculated using the mass and energy difference.

The calculated Alpha value is 1.84 x 10^15.

The transmission probability is found to be extremely small, 2.47 x 10^-29.

Despite the low probability, an alpha particle will attempt to break through the barrier 1.1 x 10^21 times per second.

The number of alpha particles breaking through per second is approximately 2.7 x 10^-8.

The calculated half-life is much longer than the observed half-life of Polonium 212.

The discrepancy is due to the assumption of a square barrier instead of an exponentially dropping one.

A more accurate model involves dividing the barrier into small sections and calculating the probability through each section.

The next video will demonstrate how to implement this more refined model for alpha decay.

The lecture provides a detailed explanation of the quantum mechanical process of alpha particle emission from a nucleus.

The use of the transmission coefficient to calculate the probability of barrier penetration is a key concept in nuclear physics.

The practical application of this model is to understand the decay process of radioactive elements, which has implications for nuclear medicine and energy production.

The lecture introduces the concept of the potential barrier and its role in the decay process of radioactive elements.

The calculation of the Alpha value and its role in determining the transmission coefficient is a crucial step in the model.

The lecture highlights the importance of accurate modeling in predicting the behavior of radioactive elements.

The lecture demonstrates the limitations of a simplified model and the need for a more complex approach to accurately predict nuclear decay rates.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (92 of 92) Modeling Polonium-212 Decay

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (76 of 92) Penetration Depth V0, E: Ex.

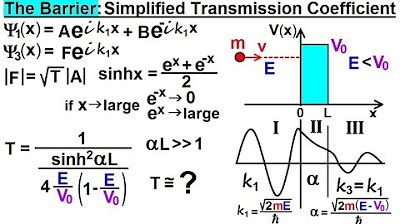
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (79 of 92) Simplified Transmission Coeff.

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (75 of 92) Penetration Depth V0, E

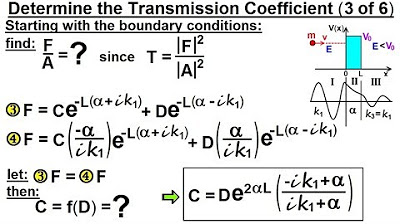
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

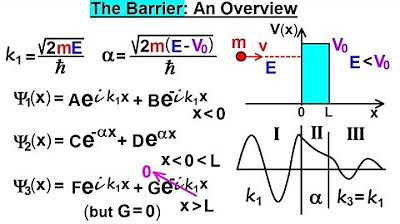
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
RadioactivityPolonium-212Alpha-ParticleBarrier-PenetrationProbability-CalculationNuclear-PhysicsLecture-ContentScientific-ModelingHalf-LifeQuantum-Mechanics