Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (75 of 92) Penetration Depth V0, E

Michel van Biezen

4 May 201810:01

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture delves into quantum mechanics, exploring the behavior of a particle with energy less than a potential step. It explains how particles can partially penetrate the potential barrier, reflected and exponentially decaying with distance. The wave function's magnitude squared is derived to describe this penetration, with a detailed mathematical process involving constants, imaginary numbers, and complex numbers. The example uses an electron approaching a 2eV potential step with 10% of that energy, leading to the calculation of the penetration depth and the probability of finding the particle within the barrier.

Takeaways

🌟 When a particle with energy less than a potential step encounters it, part of it gets reflected and another part penetrates the potential step.
📌 The penetration depth into the potential step can be described by an exponential decaying function, represented by the wave function in that region.
🔢 To calculate the magnitude of the wave function squared, which indicates the probability of finding the particle in the potential step, we need to solve for the constant C in the wave function.
🌐 The constant C is related to the portion of the wave function in region one that represents particles moving to the right, and is determined by the constants a, k1, and k2.
💡 The values of k1 and k2 are derived from the energy of the particle and the potential step, with k1 being real and k2 imaginary when the energy is less than the potential.
🔍 The magnitude of C squared is found by substituting the expressions for k1 and k2 and simplifying the resulting equation.
📈 The penetration depth is calculated by determining the value of alpha (α), which is related to the imaginary part of the wave number k2.
🌀 The value of alpha is calculated using the known mass of the particle, the energy difference from the potential step, and Planck's constant.
📊 The final equation for the probability of the particle's presence in the potential step is given by the magnitude of the wave function squared, 0.4 * e^(-2αx), where α is the calculated value and x is the distance into the potential step.
🔚 The probability of finding the particle decreases exponentially with the distance into the potential step, and future calculations will determine when this probability effectively becomes zero.
🎥 The next steps will involve calculating specific values of penetration depth for various distances to understand the probability distribution of the particle within the potential step.

Q & A

What happens when a particle with energy less than the potential step encounters the step?
-The particle will get reflected, and a portion of the particles will penetrate into the potential step, exhibiting an exponential decay in their presence as they move further into the step.
How is the penetration of the particle into the potential step described?
-The penetration is described by an exponential decaying function, which is determined by the wave function's magnitude squared in the region beyond the potential step.
What is the role of the constant C in the wave function for region two?
-The constant C is related to the constant a, which represents the portion of the wave function in region one that corresponds to particles moving to the right. C is expressed in terms of a, relative to k1 and k2.
What are k1 and k2, and how are they defined?
-k1 and k2 are wave numbers. k1 is defined as the square root of (2 times the mass times the energy of the particle) divided by h-bar, while k2 is defined similarly but related to the region where the particle's energy is less than the potential step.
How is the magnitude of C squared calculated?
-The magnitude of C squared is calculated by squaring the expression for C, which includes the wave function's components and the cancellation of h-bar and the mass (M) in the equation.
What is the significance of the potential step having a potential of two electron volts?
-The potential of two electron volts is used as an example to illustrate the calculation of the penetration depth. It provides a specific case where the energy of the particle is 10% of the potential step's energy (0.2 electron volts).
Why does k2 become an imaginary number?
-k2 becomes an imaginary number when the energy of the particle (e) minus the potential step (V) is less than zero, which occurs when the particle's energy is insufficient to overcome the potential step.
What is the role of the constant alpha in the decay function?
-Alpha is a constant that represents the imaginary part of k2 when it is negative. It is used to express the decay function in terms of a real exponent, simplifying the mathematical expression for the wave function in region two.
How is the value of alpha calculated?
-Alpha is calculated as the square root of (2 times the mass times the difference in energy, V_sub_nought minus e) divided by h-bar. The energy values are converted to joules, and the result is divided by 2 pi to find alpha.
What does the equation for the magnitude of the wave function squared (|ψ|^2) represent?
-The equation for |ψ|^2 represents the probability density of finding the particle at a certain position within the potential step, which is proportional to the magnitude of the wave function squared.
How can the penetration depth be calculated?
-The penetration depth can be calculated by using the derived equation for |ψ|^2, which includes the constant 0.4, the exponential term with alpha, and the distance X. By solving this equation for various values of X, one can determine the probability of finding the particle at different depths into the potential step.

Outlines

00:00

🌪️ Quantum Mechanics: Particle Penetration through Potential Step

This paragraph delves into the quantum mechanical scenario where a particle with energy 'e' encounters a potential step (VSIP naught). The focus is on understanding the penetration depth of the particle into the potential step despite its energy being less than the potential. The wave function's magnitude squared in the region of the step is introduced as an exponential decaying function. The process of determining the magnitude of the wave function involves calculating the constant 'C' from a previous video, understanding its relation to 'a', 'k1', and 'k2', and eventually finding the magnitude of C squared. The example uses specific values for the potential step (2 eV) and the particle's energy (0.2 eV) to illustrate the mathematical process, leading to the conclusion that the magnitude of C squared equals 0.4.

05:03

📈 Solving for Decay Function and Penetration Depth

The second paragraph continues the exploration of quantum mechanics by focusing on the decay function and penetration depth of a particle into a potential step. It explains the mathematical process of finding the value for 'I k2 X' and introduces a new constant 'alpha' to simplify the wave function in region two. The calculation involves complex numbers and the concept of imaginary numbers. The paragraph then proceeds to derive an equation for the decay function, which describes how the wave function's magnitude squared decays with distance 'X'. The constant 'alpha' is defined in terms of the mass of the particle, the potential step, and the energy difference, leading to a detailed calculation that provides a value for 'alpha'. The final step is to plug this value into the decay function to understand the particle's penetration into the potential barrier, with the aim to calculate the probability of the particle's presence at various distances in the next video.

Mindmap

Keywords

💡Energy

In the context of the video, 'energy' refers to the amount of work that can be done by a particle. It is a fundamental concept in physics that is used to describe the capacity to do work. In the given scenario, the energy of the particle is less than the potential of the step, which leads to the reflection and partial penetration of the particle into the potential step.

💡Potential Step

A 'potential step' is a type of potential energy barrier in physics where the potential energy changes abruptly by a fixed amount. It is often used to model scenarios where a particle encounters a sudden change in potential energy. In the video, the potential step is represented by 'VSIP naught', and the behavior of a particle with energy less than this potential is discussed.

💡Wave Function

The 'wave function' is a mathematical description of the quantum state of a system in quantum mechanics. It provides information about the probability of finding a particle in a particular state or position. In the video, the wave function is used to describe the probability of the particle's presence in the region beyond the potential step.

💡Exponential Decay

Exponential decay is a mathematical model that describes a quantity approaching zero at a rate proportional to its current value. In physics, it often describes how the intensity of a wave or the probability amplitude decreases with distance. In the video, the exponential decay function is used to model the decrease in the probability of finding the particle as it penetrates into the potential step.

💡Reflection

In the context of the video, 'reflection' refers to the phenomenon where a particle encounters a potential barrier and is partially reflected back. This is a wave-like behavior observed in quantum mechanics when a particle encounters a potential step that is larger than its energy.

💡Penetration

In quantum mechanics, 'penetration' refers to the ability of a particle to pass through a potential barrier, even when its energy is less than the barrier's potential. This phenomenon is contrary to classical mechanics and is described by the wave-like properties of particles in quantum mechanics.

💡Quantum Mechanics

Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. It introduces concepts like wave-particle duality, superposition, and quantum states, which are essential for understanding phenomena like particle penetration and reflection discussed in the video.

💡H-bar

H-bar, or reduced Planck's constant, is a fundamental constant in quantum mechanics that is used in equations to describe the behavior of quantum systems. It is the product of Planck's constant and 2π, and it appears in various formulas, including those for energy levels and wave functions.

💡Complex Number

A complex number is a number that can be expressed in the form of a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit with the property that i² = -1. In the context of the video, complex numbers arise when dealing with wave functions in regions where the energy is less than the potential, leading to imaginary values for k2.

💡Alpha (α)

In the context of the video, 'alpha' (α) is a constant that is defined in relation to the imaginary part of the wave function. It represents the exponential decay rate in the wave function model for the particle's penetration into the potential step.

💡Penetration Depth

The 'penetration depth' is the distance into the potential step that a particle with energy less than the step's potential can penetrate. It is a measure of how far the particle can get into the barrier before the probability of finding it there becomes effectively zero.

Highlights

The lecture discusses a scenario where a particle's energy is less than the potential of a step.

In this case, the particle encounters a potential step and gets reflected, with some particles penetrating into the step.

The penetration of particles into the potential step is described by an exponential decaying function.

The wave function in the region of the potential step is used to define the magnitude of the penetration.

The magnitude of the wave function squared is equal to an equation describing the penetration depth.

The wave function in region two is expressed in terms of constants and wave numbers.

The value of C squared is determined by substituting expressions for k1 and k2 and simplifying the equation.

The potential step is given an example value of 2 electron volts, and the particle's energy is set at 10% of that.

The magnitude of C squared is calculated to be 0.4 for the given example.

The wave function with a real exponent is derived by introducing a new constant, alpha.

Alpha is defined in terms of the mass of the particle, the potential step, and the energy of the particle.

The value of alpha is calculated for an electron with a known mass and energy.

The penetration depth equation is obtained by squaring the wave function and incorporating the value of alpha.

The equation provides a way to calculate the probability of the particle's presence within the potential barrier.

The probability of finding the particle decreases exponentially with distance into the potential step.

The decay function and penetration depth will be further explored with various values of X in the next video.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (76 of 92) Penetration Depth V0, E: Ex.

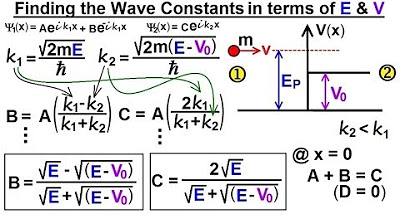
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (66 of 92) B=? C=? in terms of E & V0

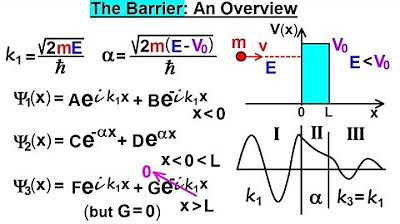
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

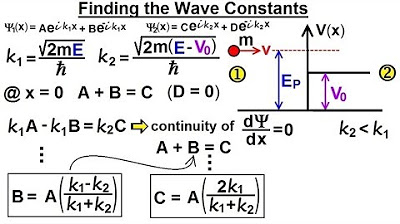
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (65 of 92) Wave Constants B=? C=?

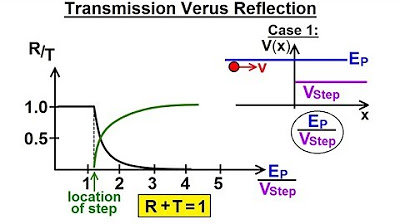
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (62 of 92) Transmission vs Reflection

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (75 of 92) Penetration Depth V0, E

Takeaways

Q & A

What happens when a particle with energy less than the potential step encounters the step?

How is the penetration of the particle into the potential step described?

What is the role of the constant C in the wave function for region two?

What are k1 and k2, and how are they defined?

How is the magnitude of C squared calculated?

What is the significance of the potential step having a potential of two electron volts?

Why does k2 become an imaginary number?

What is the role of the constant alpha in the decay function?

How is the value of alpha calculated?

What does the equation for the magnitude of the wave function squared (|ψ|^2) represent?

How can the penetration depth be calculated?