Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (57 of 92) Calculating Hermite Polynomial?

Michel van Biezen
15 Apr 201805:44
EducationalLearning
32 Likes 10 Comments

TLDRThe transcript outlines the process of calculating Hermitian polynomials, starting from the 0th state and progressing to higher states. It demonstrates the derivation of the first three polynomials using derivatives of the function e^(-x^2). The explanation is detailed, showing the step-by-step mathematical operations involved in obtaining the polynomials for N=0, N=1, and N=2. The lecture also hints at the complexity involved in deriving polynomials for higher states and the importance of normalizing these functions for a complete solution to the quantum mechanical oscillator problem, as derived from the Schrödinger equation.

Takeaways
  • 📚 The lecture introduces the calculation of Hermitian polynomials using the differential operator method.
  • 🌟 For N=0, the 0th Hermitian polynomial is derived as 1, by applying the 0th derivative to the function e^(-x^2).
  • 🔢 For N=1, the 1st Hermitian polynomial is calculated as 2x, obtained by taking the first derivative and simplifying the expression.
  • 📈 For N=2, the 2nd Hermitian polynomial is found to be 4x^2 - 2, after taking the second derivative and simplifying the result.
  • 🧠 The pattern for calculating Hermitian polynomials involves taking successive derivatives of the function e^(-x^2).
  • 🔄 The process of calculating Hermitian polynomials becomes more complex with increasing values of N.
  • 🌐 The lecture also mentions the importance of normalizing these polynomials for a complete solution to the quantum mechanical oscillator problem.
  • 📊 The normalization of the Hermitian polynomials is a topic that will be covered later in the lecture series.
  • 📖 The script is based on a mathematical approach to solving the Schrödinger equation for the harmonic oscillator.
  • 🎓 The content is suitable for individuals with a strong background in mathematics and quantum mechanics.
  • 🔑 Key to understanding the script is recognizing the pattern in the differentiation process and the application of exponential functions.
Q & A

  • What is the starting point for calculating the Hermitian polynomials?

    -The starting point for calculating the Hermitian polynomials is with N equals 0, which represents the 0 state.

  • What is the expression for the 0 state of the Hermitian polynomial?

    -The expression for the 0 state of the Hermitian polynomial is (-1)^0 times e^(x^2) times the 0 derivative of e^(-x^2), which simplifies to 1.

  • How does the 0 state derivative of a function relate to the function itself?

    -The 0 state derivative of a function relates to the function itself by the fact that any number to the 0 power is 1, so the 0 derivative of a function simply returns the function.

  • What is the expression for the 1 state Hermitian polynomial?

    -The expression for the 1 state Hermitian polynomial is 8 sub 1 of x, which is (-1)^1 times e^(x^2) times the first derivative of e^(-x^2), simplifying to 2x.

  • How do you find the second derivative of e^(-x^2)?

    -To find the second derivative of e^(-x^2), you first take the first derivative, and then take the derivative of that result again, which involves applying the chain rule twice.

  • What is the expression for the 2 state Hermitian polynomial?

    -The expression for the 2 state Hermitian polynomial is (-1)^2 times e^(x^2) times the second derivative of e^(-x^2), which simplifies to 4x^2 - 2.

  • How does the pattern of Hermitian polynomials help in calculating them for higher N states?

    -The pattern of Hermitian polynomials shows that for each higher N state, you need to take the Nth derivative of e^(-x^2) and apply the appropriate power of (-1) and x terms, which helps in systematically calculating the polynomials for higher N values.

  • What is the significance of normalizing the Hermitian polynomials?

    -Normalizing the Hermitian polynomials is important because it ensures that the functions form an orthogonal set, which is a requirement for solving the quantum mechanical oscillator problem derived from the Schrödinger equation.

  • Why does the process of finding Hermitian polynomials become complicated for higher N states?

    -The process becomes complicated for higher N states because each step involves taking more derivatives and dealing with increasingly complex algebraic expressions, which requires more time and effort.

  • What is the role of the Hermitian polynomials in quantum mechanics?

    -In quantum mechanics, Hermitian polynomials play a crucial role in describing the wave functions of particles in a harmonic oscillator, which is a fundamental system in quantum mechanics.

  • How does the lecture script help in understanding the mathematical structure of Hermitian polynomials?

    -The lecture script provides a step-by-step derivation of the Hermitian polynomials, which helps in understanding the mathematical structure by showing the process of obtaining each polynomial from the previous one and highlighting the pattern that emerges.

Outlines
00:00
📚 Introduction to Hermitian Polynomials

This paragraph introduces the calculation of Hermitian polynomials, starting with the case where N equals 0, which represents the 0th state. The explanation begins with the derivation of the first polynomial, highlighting that the 0th derivative of a function returns the function itself, leading to the result of 1 for the polynomial. The process is then repeated for N equals 1, resulting in the second polynomial. The explanation is detailed, walking through the steps of taking derivatives and applying them to the exponential function. The paragraph concludes with the derivation of the third polynomial, emphasizing the pattern and method used to obtain the Hermitian polynomials.

05:02
🔢 Derivation and Normalization of Hermitian Polynomials

This paragraph continues the discussion on Hermitian polynomials, focusing on the process of deriving them for higher values of N, specifically N equals 4. It acknowledges the increasing complexity as more derivatives are taken but reassures that the pattern becomes clear with practice. The paragraph also mentions the importance of normalizing these polynomials to complete the solution for the quantum mechanical oscillator, which is derived from the Schrödinger equation. The speaker encourages the audience to stay tuned for the next part of the lecture, where normalization will be demonstrated.

Mindmap
Keywords
💡Hermitian Polynomials
Hermitian Polynomials are a set of orthogonal polynomials that are solutions to the Hermite differential equation. They are used in various fields of mathematics and physics, including quantum mechanics. In the video, the lecturer is calculating the first few Hermitian polynomials for different values of N, starting from the 0 state, which demonstrates the process of deriving these polynomials and their role in solving the Schrödinger equation for the harmonic oscillator.
💡Derivative
In calculus, a derivative represents the rate of change of a function with respect to its independent variable. It is a fundamental concept used in the analysis of functions and their behavior. In the context of the video, the derivative is used to find the successive terms of the Hermitian polynomials by differentiating the exponential function e^(-x^2) multiple times.
💡Exponential Function
An exponential function is a mathematical function where the base, e, is a constant approximately equal to 2.71828. It is used to model growth or decay processes and is a fundamental concept in calculus. In the video, exponential functions are used in the form of e^(x^2) and e^(-x^2) to construct the Hermitian polynomials through differentiation.
💡Normalization
Normalization in the context of functions refers to the process of adjusting a function so that its integral over a certain domain equals 1. This is particularly important in quantum mechanics, where wave functions need to be normalized to ensure that the probabilities sum up to 1. The video script mentions that after finding the Hermitian polynomials, the next step is to show how to normalize them, which is crucial for their application in the quantum mechanical oscillator model.
💡Quantum Mechanics
Quantum Mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the atomic and subatomic scales. It uses mathematical models, such as wave functions and Schrödinger equations, to predict the probabilities of different outcomes in physical systems. The video's discussion of Hermitian polynomials and the quantum mechanical oscillator is rooted in the principles of Quantum Mechanics.
💡Harmonic Oscillator
A harmonic oscillator is a system that oscillates at a constant frequency and is driven by a restoring force that is proportional to the displacement from its equilibrium position. In physics, it is a model system used to understand wave-like behavior and is fundamental in quantum mechanics. The video discusses the Hermitian polynomials in the context of the quantum mechanical oscillator, which is a system governed by the Schrödinger equation.
💡Schrödinger Equation
The Schrödinger Equation is a fundamental equation in Quantum Mechanics that describes how the quantum state of a physical system changes with time. It is used to determine the wave function of a system, which provides information about the probabilities of finding particles in different states. The video's discussion of Hermitian polynomials is in the context of solving the Schrödinger Equation for the harmonic oscillator.
💡Power
In mathematics, the power of a number refers to the result of multiplying that number by itself a certain number of times. It is denoted as a^n, where a is the base and n is the exponent. In the video, the power is used in the context of the Hermitian polynomials, where the讲师 calculates the polynomials for different powers of -1 (e.g., -1 to the power of 0, 1, and 2).
💡Integral
In calculus, an integral represents the accumulation of a quantity, calculated as the limit of the sum of infinitesimal inputs. Integrals are used to find the area under a curve, the total value of a quantity, or to solve differential equations. In the video, the integral is not directly mentioned but is implied in the context of the Hermitian polynomials, which are solutions to differential equations and are part of the process of normalizing functions to integrate to 1.
💡Wave Function
In Quantum Mechanics, a wave function is a mathematical description of the quantum state of a system. It provides information about the probabilities of finding a particle in a particular state or location. The Hermitian polynomials are part of the solutions to the wave functions in the context of the quantum mechanical oscillator model.
💡Pattern
In mathematics, a pattern refers to a sequence of numbers or shapes that follow a specific rule or sequence. In the video, the lecturer is demonstrating a pattern in the calculation of Hermitian polynomials by showing how the polynomials change with increasing values of N. Recognizing this pattern is crucial for understanding the general form of the Hermitian polynomials and for calculating them for higher values of N without having to compute each term from scratch.
Highlights

Introduction to the calculation of Hermitian polynomials.

Derivation of the 0th Hermitian polynomial with N equals 0.

Explanation of the 0th derivative resulting in the original function.

Calculation of the 1st Hermitian polynomial for N equals 1.

Derivation process involving the first and second derivatives.

Result of the 1st Hermitian polynomial: 2x * e^(-x^2).

Derivation of the 2nd Hermitian polynomial for N equals 2.

Complex calculation involving multiple steps of differentiation.

Final expression for the 2nd Hermitian polynomial: 4x^2 - 2.

Observation of the pattern for obtaining Hermitian polynomials.

Mention of the process becoming more complicated for higher N values.

Connection to the quantum mechanical oscillator derived from the Schrödinger equation.

Promise of an upcoming explanation on how to normalize the Hermitian polynomials.

Emphasis on the importance of understanding the normalization process for a complete solution.

The lecture provides a step-by-step method for calculating Hermitian polynomials.

The use of derivatives to construct higher order Hermitian polynomials.

The significance of the Hermitian polynomials in quantum mechanics.

Transcripts

Browse More Related Video

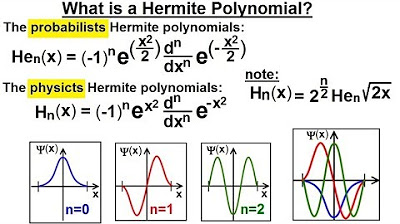
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (56 of 92) What is a Hermite Polynomial?

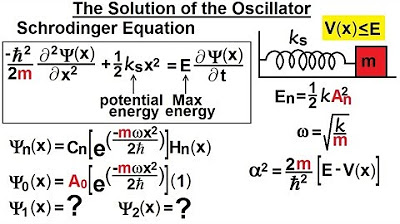
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

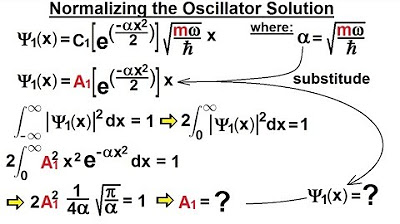
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (60 of 92) Normalizing the Oscillator

AP Calculus BC Lesson 10.11 Part 1

Writing Polynomial Functions With Given Zeros | Precalculus

Complex Numbers: Operations, Complex Conjugates, and the Linear Factorization Theorem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Hermitian PolynomialsQuantum MechanicsDerivationsMathematics LectureOnline LearningEducational ContentAdvanced MathPhysics ConceptsSchrödinger EquationNormalization