Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (53 of 92) The wave Equation

Michel van Biezen
11 Apr 201803:01
EducationalLearning
32 Likes 10 Comments

TLDRThe lecture discusses the wave function of a quantum harmonic oscillator, emphasizing the sine and cosine relationship with its second derivative. It explains that the wave function's shape is influenced by the quantum state's energy, with higher states leading to greater oscillation amplitudes. The function must asymptotically reach the x-axis and exhibit more oscillations with increasing quantum states. The probability density, derived from squaring the wave function, is always positive, confirming the physical validity of the wave function's form. Solving the differential equation further validates these insights, providing a clear understanding of the harmonic oscillator's wave functions.

Takeaways
  • 📌 The Shirley equation helps visualize the wave function of a harmonic oscillator.
  • 🌐 The wave function has a sine and cosine relationship with its second derivative.
  • 🔢 The quantity alpha squared is positive, indicating the total energy is greater than or equal to the potential energy.
  • 💫 Quantum states (N, n) determine the amplitude of oscillation, with higher states having greater amplitude.
  • 📈 As quantum states increase, the wave function exhibits more oscillations.
  • 📊 The wave function must asymptotically reach the x-axis on both sides of the vertical axis representing position X.
  • 🌈 The probability density function of the wave function is represented by the squared wave function, ensuring positivity.
  • 📌 The shape of the wave function is constrained by the conditions it must meet, such as reaching the x-axis.
  • 🔍 Even without solving the differential equation, the general form of the wave function can be inferred from its conditions.
  • 🧩 Solving the differential equation confirms the initial estimate of the wave function's shape.
  • 📈 The wave function's lobes increase with each quantum state: one lobe for n=1, two for n=2, and so on.
Q & A

  • What is the Shirley equation mentioned in the script?

    -The Shirley equation is not explicitly defined in the script, but it is implied to be a mathematical representation of the harmonic oscillator, involving the wave function and its second derivative.

  • How does the presence of a sine and cosine relationship in the wave function help in understanding the harmonic oscillator?

    -The sine and cosine relationship simplifies the understanding of the wave function's behavior in the context of the harmonic oscillator by relating it to the second derivative of the wave function, which is a common pattern in oscillatory systems.

  • What is the significance of alpha squared being a positive quantity in the context of the harmonic oscillator?

    -Alpha squared being positive ensures that the total energy of the oscillator is always greater than or equal to the potential energy, which is a fundamental requirement in quantum mechanics for stable states.

  • How do the amplitudes of oscillation vary with different quantum states?

    -The amplitudes of oscillation vary depending on the total energy of the oscillator, with higher quantum states (N = 2, N = 3, etc.) having greater amplitudes, indicating more energetic oscillations.

  • What are the conditions that a wave function must meet according to the script?

    -The wave function must asymptotically reach the x-axis on both sides of the vertical axis representing position X, and it must represent the correct number of oscillations for the given quantum state.

  • How does the probability density function relate to the wave function?

    -The probability density function is the square of the wave function, ensuring that all values are positive, which is necessary for interpreting the wave function in terms of probabilities in quantum mechanics.

  • What does the script imply about the shape of the wave function for different energy states?

    -The script implies that the shape of the wave function is determined by the number of lobes, which increases with the quantum state, following a pattern of (n+1) lobes for the n-th energy level.

  • Why is it said that there is only one way to draw the wave function for the various energy states?

    -There is only one way to draw the wave function because it must asymptotically reach the x-axis and have the correct number of lobes according to the quantum state, which dictates a unique shape for each energy level.

  • What role does solving the differential equation play in understanding the wave function?

    -Solving the differential equation confirms the initial estimate of the wave function's shape and validates the understanding of how the wave function changes with different energy states.

  • How does the script describe the representation of wave functions for the simple harmonic oscillator?

    -The script describes the representation of wave functions as a series of shapes with increasing lobes corresponding to the energy states, starting with one lobe for the ground state and adding lobes as the energy state increases.

Outlines
00:00
📚 Understanding the Wave Function of the Harmonic Oscillator

This paragraph discusses the complexities of visualizing the wave function from the Shirley equation of the harmonic oscillator. It explains that by rewriting the equation, one can identify a sine and cosine relationship between the wave function and its second derivative, provided that the quantity alpha squared is positive, which is always the case since total energy exceeds potential energy. The amplitude of oscillation varies with quantum states, with higher states corresponding to greater amplitudes. The wave function must asymptotically reach the x-axis on both sides and exhibit more oscillations with higher quantum states. The probability of the wave function, obtained by squaring it, must always be positive. The paragraph concludes by emphasizing that without solving the differential equation, one can still deduce the shape of the wave function for various energy states, with the function's form becoming more apparent as one progresses through the energy levels.

Mindmap
Keywords
💡Shirley equation
The Shirley equation is a mathematical representation used in quantum mechanics to describe the energy states of a simple harmonic oscillator. In the context of the video, it is used to illustrate the relationship between the wave function and the second derivative of the wave function. The equation helps in visualizing the wave function's shape and understanding the behavior of quantum states.
💡Wave function
A wave function is a mathematical function that describes the quantum state of a system in quantum mechanics. It contains all the information about the system and is used to calculate the probabilities of finding a particle in a particular state. In the video, the wave function is central to understanding the behavior of the harmonic oscillator and how its shape changes with different energy levels.
💡Harmonic oscillator
A harmonic oscillator is a system that oscillates at a constant frequency and experiences a restoring force proportional to its displacement from an equilibrium position. In quantum mechanics, the simple harmonic oscillator is an important model system with quantized energy levels. The video uses the harmonic oscillator to explain quantum states and wave functions.
💡Quantum states
Quantum states are the various conditions that a quantum system can be in, each characterized by a unique set of quantum numbers. These states determine the properties of the system, such as energy levels and wave functions. In the video, quantum states are associated with the energy levels of the harmonic oscillator, with higher states corresponding to greater amplitudes of oscillation.
💡Amplitude
Amplitude in the context of wave functions refers to the maximum value of the wave, which can be interpreted as the 'height' of the wave. In quantum mechanics, the amplitude of a particle's wave function is related to the probability of finding the particle in a particular state. The video discusses how the amplitude of the harmonic oscillator's wave function varies with different quantum states.
💡Probability density function
The probability density function (PDF) in quantum mechanics is the square of the absolute value of the wave function. It represents the probability of finding a particle within a certain range of positions. The PDF must always be positive, which means that the wave function, when squared, ensures that all probabilities are non-negative.
💡Quantum mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. It introduces concepts like wave-particle duality, quantization of energy, and superposition of states. The video's content is rooted in quantum mechanics principles, particularly as they apply to the simple harmonic oscillator.
💡Second derivative
The second derivative of a function is the derivative of its first derivative. It measures how the rate of change of a function is changing. In the context of the video, the second derivative of the wave function is related to the sine and cosine relationship, which is crucial for understanding the shape and behavior of the wave function in a harmonic oscillator.
💡Total energy
In the context of the simple harmonic oscillator, the total energy is the sum of the kinetic and potential energies of the system. It is always greater than or equal to the potential energy alone. The total energy determines the quantum states and, consequently, the amplitude of the oscillation in quantum mechanics.
💡Differential equation
A differential equation is an equation that relates a function with its derivatives. In physics and engineering, they are often used to describe the behavior of systems over time or space. In the video, solving the differential equation associated with the harmonic oscillator confirms the shape of the wave function and helps in understanding its properties.
💡Asymptotic behavior
Asymptotic behavior refers to the behavior of a function as it approaches a certain value or infinity. In the context of the video, it describes how the wave function of the harmonic oscillator approaches the x-axis on both sides of the vertical axis, indicating the limits of the wave function's spread.
Highlights

Understanding the Shirley equation of the harmonic oscillator provides insight into the wave function's appearance.

The wave function's relationship with the second derivative involves sine and cosine, simplifying its visualization.

The quantity alpha squared is positive, a crucial aspect since total energy is always greater than or equal to potential energy.

Quantum mechanics dictates that amplitudes vary based on the total energy of the oscillator and quantum states.

Higher quantum states (N equals 0, 1, 2, etc.) correspond to greater amplitudes of oscillation.

Certain conditions must be met when visualizing the wave function, such as asymptotically reaching the x-axis on both sides.

The wave function's oscillations increase with higher quantum states.

Squaring the wave function for probability calculations ensures all values are positive.

The shape of the wave function is constrained by the requirement to asymptotically reach the x-axis, limiting the ways it can be drawn.

Even without solving the differential equation, the form and shape of the wave function can be deduced.

Solving the differential equation confirms the initial estimate of the wave function's shape.

The wave function's representation is clear and consistent across various energy states, with lobes increasing in number.

The probability density function is represented by the wave function's lobes, each corresponding to a quantum state.

The wave function's drawing for different energy states is guided by the quantum mechanics principles.

The Shirley equation facilitates a deeper understanding of the harmonic oscillator's quantum behavior.

The wave function's visualization is essential for comprehending quantum states and their properties.

This lecture provides a comprehensive overview of the harmonic oscillator's wave functions and their quantum state representations.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (52 of 92) A Closer Look at the Equation

21. Quantum Mechanics III

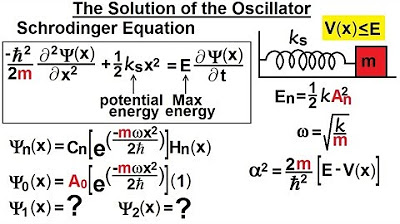
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (55 of 92) Solution of the Oscillator

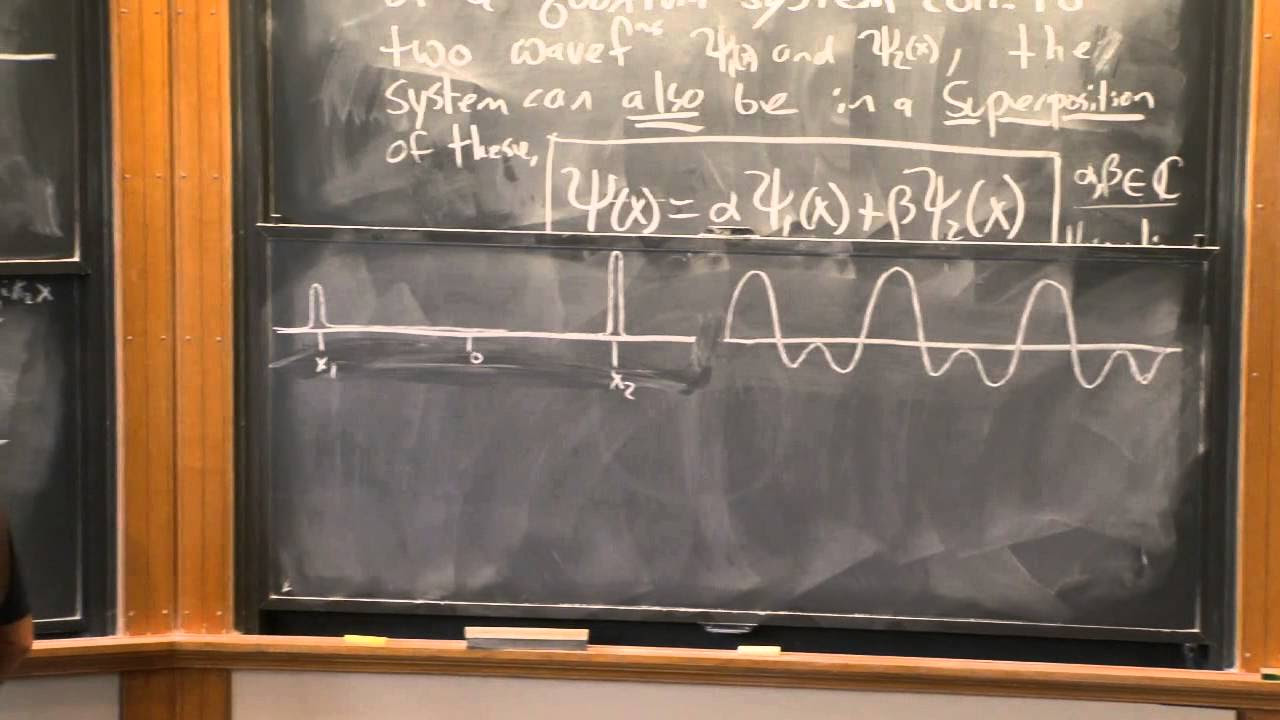
Lecture 3: The Wave Function

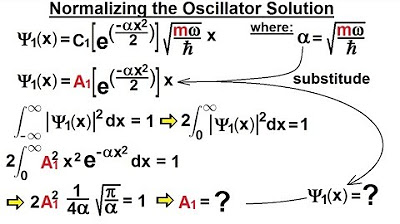
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (60 of 92) Normalizing the Oscillator

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (19 of 92) Particle in 1-D Box: Example 1/2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsHarmonicOscillatorsWaveFunctionsEnergyStatesProbabilityDensitiesSineCosineQuantumStatesAmplitudeOscillationDifferentialEquationsPhysicsLecture