AP Calculus BC Lesson 10.4
TLDRIn this lesson, the integral test for determining the convergence or divergence of an infinite series is explored. The test is applicable if the function f(x) is positive, continuous, and decreasing for x ≥ K. The video demonstrates the application of the integral test through examples, highlighting that it only determines convergence or divergence, not the value to which a series converges. The lesson emphasizes the importance of verifying the conditions for the integral test before application and compares its efficiency with other convergence tests.
Takeaways
- 📚 The integral test is a method to determine the convergence or divergence of an infinite series by comparing it to the integral of a related function.
- 🔍 The function for the integral test must be positive, continuous, and decreasing for the test to be applicable, specifically for values greater than or equal to a certain lower bound K.
- 🌟 If the integral from K to infinity converges, the series also converges; if the integral diverges, so does the series.
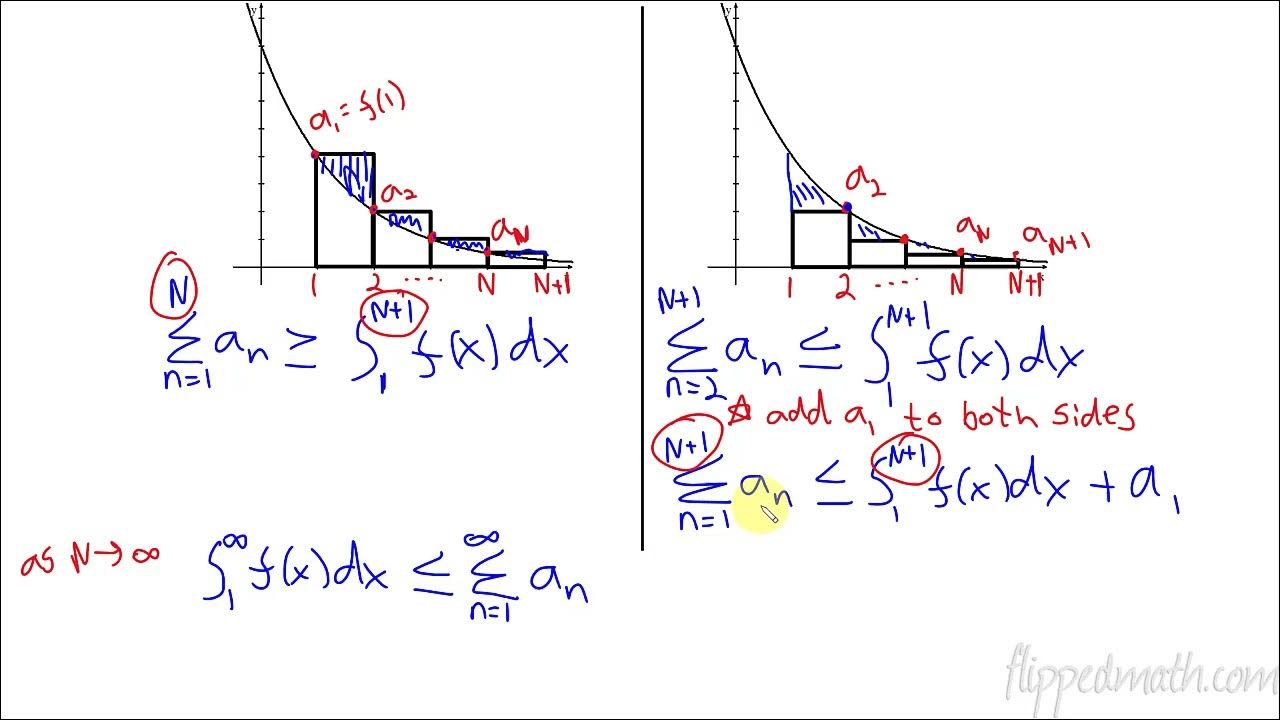
- 📈 The integral test is based on the concept of representing the series as a left-hand Riemann sum, where the series value is greater than or equal to the integral value.
- 🛠️ To apply the integral test, one must verify the positivity, continuity, and decreasing nature of the function f(x) for x ≥ K.
- 📝 The integral test does not provide the value to which the series converges, only whether it does or does not converge.
- 🚫 The integral test is not the most efficient for determining convergence since it requires proving the function's properties and calculating an improper integral.
- 🧐 For the series ∑(2/(n-3)) from n=4 to ∞, the integral test shows that it diverges because the integral from 4 to ∞ of 2/(x-3) dx diverges.
- 📊 For the series ∑(n/e^n) from n=1 to ∞, the integral test confirms convergence since the integral from 1 to ∞ of x/e^x dx converges.
- ✅ The integral test can be applied to functions where the series terms a_n are derived directly from the function f(x), replacing n with x.
- 📌 The integral test is not universally applicable; it cannot be used for series that do not meet the conditions of positivity, continuity, and decreasing nature of the related function.
Q & A
What is the integral test and its basic premise?
-The integral test is a method used to determine the convergence or divergence of an infinite series. The basic premise is that if a positive continuous and decreasing function f(x) satisfies certain conditions for x greater than or equal to a lower bound K, then the integral from K to infinity of f(x) and the series from n=K to infinity of a_n will either both converge or both diverge.
What are the three conditions that must be met for the integral test to be applicable?
-For the integral test to be applicable, the function f(x) must be positive, continuous, and decreasing for all x values greater than or equal to a lower bound K.
How does the integral test relate to the concept of a Riemann sum?
-The integral test is related to the concept of a Riemann sum because it involves representing the series as a left-hand Riemann sum. The idea is that the series is essentially the sum of the areas of rectangles under the curve of the function f(x), and the integral gives the actual area under the curve. If the integral converges, then the series, represented by the sum of the areas of the rectangles, will also converge.
What happens when the integral from K to infinity of f(x) diverges?
-If the integral from K to infinity of f(x) diverges, then the series from n=K to infinity of a_n will also diverge. The integral test does not provide the value to which the series converges, but it does determine the convergence or divergence of the series.
How does the integral test compare to other convergence tests in terms of efficiency?
-The integral test is not the most efficient method for determining convergence or divergence because it requires proving that f(x) is positive, continuous, and decreasing before it can be applied. Additionally, it involves calculating an improper integral, which can be time-consuming. Other tests may provide faster results, especially for multiple-choice questions.
What is the significance of the function f(x) being positive in the integral test?
-The significance of f(x) being positive in the integral test is that it ensures the function's values are greater than zero for the range of x being considered. This is crucial for the convergence or divergence analysis because it affects the area under the curve, which is the integral, and the sum of the series' terms.
How does the integral test determine the convergence or divergence of the series from n=4 to infinity of 2/(n-3)?
-The integral test determines the convergence or divergence of the series by comparing it to the integral from 4 to infinity of the function f(x) = 2/(x-3). By verifying that f(x) is positive, continuous, and decreasing for x greater than or equal to 4, and then evaluating the improper integral, the test can conclude that if the integral diverges, the series also diverges.
What is the role of the derivative of the function f(x) in the integral test?
-The derivative of the function f(x), denoted as f'(x), plays a crucial role in the integral test as it is used to determine whether f(x) is decreasing for the relevant interval. A negative derivative indicates that the function is decreasing, which is one of the necessary conditions for the integral test to be applicable.
What is the significance of the lower bound K in the integral test?
-The lower bound K in the integral test is the starting point for the function f(x) and the series a_n to be considered. It is the value of x from which the function must be positive, continuous, and decreasing for the integral test to be applicable. For the series, it corresponds to the starting term n=K.
How does the integral test apply to the series from n=1 to infinity of n/e^n?
-The integral test applies to the series by comparing it to the integral from 1 to infinity of the function f(x) = x/e^x. After verifying that f(x) is positive, continuous, and decreasing for x greater than or equal to 1, the integral is evaluated. Since the integral converges, the series also converges by the integral test.
What is the main limitation of the integral test for determining the convergence or divergence of a series?
-The main limitation of the integral test is that it does not determine the exact value to which a convergent series converges. It only provides information about whether the series converges or diverges. Additionally, it requires the function to be positive, continuous, and decreasing, which may not always be the case for a given series.
Outlines
📚 Introduction to the Integral Test
The video begins with an introduction to the integral test, a method for determining the convergence or divergence of an infinite series. The test is applicable when the function f(x) is positive, continuous, and decreasing for x greater than or equal to a lower bound K. The integral test states that if the integral of f(x) from K to infinity converges, then the series converges, and if the integral diverges, the series diverges as well. The video emphasizes the three conditions necessary for applying the integral test and explains the concept using the representation of a series as a left-hand Riemann sum.
🧐 Applying the Integral Test to a Specific Series
The video proceeds to apply the integral test to the series ∑(n=4 to ∞) of 2/(n-3). It explains the need to set a_n equal to f(x) and verifies that f(x) = 2/(x-3) is positive, continuous, and decreasing for x ≥ 4. The video then demonstrates how to compute the integral from 4 to infinity of f(x)dx and concludes that since the integral diverges, the series also diverges. It also notes that the integral test does not determine the value to which the series converges and that it may not be the most efficient method for all cases.
📈 Testing Functions for the Integral Test
The video discusses the process of verifying whether a function meets the criteria for the integral test. It explains how to check if a function is positive, continuous, and decreasing for x ≥ 1. The video uses the function f(x) = x/e^x as an example and shows that it satisfies all three conditions. It then sets up the integral from 1 to infinity of x/e^x dx to determine the series' convergence or divergence, highlighting the importance of understanding improper integrals for this process.
🔢 Solving Improper Integrals with Integration by Parts
The video addresses the challenge of evaluating improper integrals, specifically the integral from 1 to infinity of x/e^x dx. It introduces integration by parts as a method to solve this integral, carefully selecting u and dv, and applying the integration by parts formula. The video shows the step-by-step process of evaluating the antiderivative and the limit as T approaches infinity, ultimately concluding that the integral converges, indicating that the series also converges.
💡 Understanding the Limitations of the Integral Test
The video explores the limitations of the integral test through multiple-choice questions. It explains which series do not meet the conditions for the integral test to be applied, focusing on the necessity of the function being positive, continuous, and decreasing. The video also demonstrates how to apply the integral test to different series, emphasizing the importance of verifying the conditions for each specific case.
🧠 Critical Analysis of Functions for the Integral Test
The video delves into a critical analysis of functions to determine their suitability for the integral test. It examines the function f(x) = (8x + 7) / (x + 2)(x - 1) and verifies its positivity, continuity, and decreasing nature for x ≥ 3. The video then finds the derivative of the function to confirm that it is decreasing on the interval from 3 to infinity. The detailed explanation includes the calculation of the integral and the application of the integral test to conclude that the corresponding series diverges.
📝 Free Response Question: Integral Test Application
The video concludes with a free response question that applies the integral test to a given function and series. It reiterates the importance of verifying the conditions for the integral test and demonstrates the process of evaluating the integral from 3 to infinity of the function. The video shows that the integral diverges, leading to the conclusion that the series also diverges, and emphasizes the conditions under which the integral test was used to determine this result.
Mindmap
Keywords
💡Infinite Series
💡Convergence
💡Divergence
💡Integral Test
💡Positive Continuous Decreasing Function
💡Riemann Sum
💡Improper Integral
💡Vertical Asymptote
💡Quotient Rule
💡Natural Logarithm
💡Limit
Highlights
The integral test is introduced as a method to determine the convergence or divergence of an infinite series.
For the integral test to apply, the function f(x) must be positive, continuous, and decreasing for x ≥ K.
The integral test states that if the integral from K to infinity of f(x)dx converges, the series also converges; if it diverges, the series diverges too.
The integral test does not provide the value to which the series converges, only that it does or does not.
The series is represented as a left-hand Riemann sum, with the function's decreasing nature affecting the comparison between the series and the integral.
An example is provided where the series from n=4 to infinity of 2/(n-3) is tested for convergence using the integral test.
The function f(x) = 2/(x-3) is verified to be positive, continuous, and decreasing for x ≥ 4.
The integral from 4 to infinity of f(x)dx is shown to diverge, indicating that the series also diverges.
Another example involves the series from n=1 to infinity of n/e^n, which is tested for convergence.
The function f(x) = x/e^x is confirmed to be positive, continuous, and decreasing for x ≥ 1.
The integral from 1 to infinity of f(x)dx is demonstrated to converge, implying the series also converges.
The integral test is not always the most efficient method for determining convergence or divergence due to the need to prove the function's properties and calculate an improper integral.
Multiple-choice questions (MCQs) related to the integral test are presented to assess understanding of its application.
A function g(x) is given, and it is determined that the integral from 1 to infinity of g(x)dx converges to a value of 9.
The series from n=1 to infinity of g(n) is shown to converge and be greater than or equal to the value of the integral.
A free-response question involves a function f(x) = (8x + 7) / (x + 2)(x - 1) and its integral from 3 to infinity is determined to diverge.
The series from n=3 to infinity of (8n + 7) / (n + 2)(n - 1) is also shown to diverge by the integral test.
The integral test conditions are restated for clarity and emphasis in the context of the free-response question.
Transcripts
Browse More Related Video

Calculus 2 Lecture 9.3: Using the Integral Test for Convergence/Divergence of Series, P-Series
Calculus Chapter 5 Lecture 51 Convergence Tests 1
Calculus BC – 10.4 Integral Test for Convergence

Integral Test and p-Series

Infinite Series Multiple Choice Practice for Calc BC (Part 6)

Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test
5.0 / 5 (0 votes)
Thanks for rating: