Video 80 - Curvature Tensor - Part 2

Tensor Calculus
5 Jun 202215:39
EducationalLearning
32 Likes 10 Comments

TLDRIn this video on tensor calculus, the presenter demonstrates how to derive principal curvatures from a curvature tensor for a surface. They explain the calculation of mean and Gaussian curvatures, and the process of diagonalizing a matrix to find eigenvalues, which represent the principal curvatures. The video also illustrates how to apply these concepts to sample surfaces like a cylinder, sphere, and torus, highlighting the simplicity and power of tensor calculus in analyzing curved surfaces.

Takeaways
  • 📚 The video continues the discussion on tensor calculus, focusing on using the curvature tensor to derive principal curvatures of a surface.
  • 🧩 The mean curvature is found by contracting the diagonal elements of the curvature tensor, summing them up to get a single value.
  • 📐 The Gaussian curvature is the determinant of the curvature tensor, calculated as the product of the diagonal elements minus the product of the off-diagonal elements.
  • 🔍 If the curvature tensor is in diagonal form, the diagonal elements are the principal curvatures, but this is not always the case and requires diagonalization.
  • 🔢 The number of eigenvalues for a matrix is equal to its dimension; for a 2x2 matrix, two eigenvalues are expected, and the formula provided is specific to 2x2 matrices.
  • 🌐 Diagonalizing a matrix involves finding its eigenvalues and using them to construct an equivalent matrix with only diagonal elements, which simplifies finding the principal curvatures.
  • 📉 The eigenvalues of the given matrix example are calculated to be 8 and -1, indicating the principal curvatures of the surface.
  • 🔄 Diagonalizing a matrix is akin to rotating the coordinate axes until off-diagonal elements become zero, simplifying the understanding of curvature properties.
  • 📈 The video demonstrates the application of these concepts on sample surfaces like a cylinder, sphere, and torus, showing how to calculate mean curvature, Gaussian curvature, and principal curvatures.
  • 🔄 The process of working with the curvature tensor is shown to be simpler and more direct than transforming functions or rotating axes in different coordinate systems.
  • 📊 The intrinsic curvature properties of different surfaces, such as a cylinder being intrinsically flat with zero Gaussian curvature, are highlighted.
Q & A

  • What is the main topic discussed in this video?

    -The main topic discussed in this video is the use of the curvature tensor to derive the principal curvatures of a surface in the context of tensor calculus.

  • What is the formula for calculating the mean curvature from the curvature tensor?

    -The mean curvature is calculated by forming the contraction of the curvature tensor, which is the summation of the diagonal elements, denoted as b_alpha_alpha in the script.

  • How is the Gaussian curvature related to the curvature tensor?

    -The Gaussian curvature is equal to the determinant of the matrix representation of the curvature tensor with one upper index and one lower index.

  • What is the significance of diagonalizing a matrix in the context of this video?

    -Diagonalizing a matrix allows us to find the principal curvatures when the curvature tensor is not already in diagonal form. It involves finding the eigenvalues of the matrix and using them to construct an equivalent diagonal matrix.

  • What is the formula for finding the eigenvalues of a 2x2 matrix as presented in the video?

    -The formula for the eigenvalues of a 2x2 matrix is lambda = (1/2) * (sum of b11 and b22) ± (1/2) * sqrt((b11 - b22)^2 + 4 * b12 * b21).

  • How are the principal curvatures related to the eigenvalues of the curvature tensor?

    -The principal curvatures are the eigenvalues of the curvature tensor when it is diagonalized. They represent the curvature along the principal directions of the surface.

  • Why is the determinant of a diagonalized matrix equal to the product of its diagonal elements?

    -The determinant of a diagonal matrix is the product of its diagonal elements because the determinant is calculated as the product of the eigenvalues when the matrix is in diagonal form.

  • What does it mean for a matrix to be in diagonal form?

    -A matrix is in diagonal form when all off-diagonal elements are zero, and only the diagonal elements are non-zero. This simplifies calculations and makes it easy to identify the principal curvatures.

  • How does the video demonstrate the process of deriving invariant properties from the curvature tensor?

    -The video demonstrates the process by showing the steps to calculate the mean curvature, Gaussian curvature, and principal curvatures using the curvature tensor of various sample surfaces like a cylinder, a sphere, and a torus.

  • What is the intrinsic curvature of a cylinder according to the video?

    -The intrinsic curvature of a cylinder is zero because it can be unfolded into a flat surface, indicating that it has no Gaussian curvature.

  • How does the curvature tensor simplify the process of working with curved surfaces compared to other methods?

    -The curvature tensor simplifies the process by providing a direct application of its components to derive invariant properties without the need to transform functions to various coordinate systems or rotate axes to eliminate mixed derivatives.

Outlines
00:00
📚 Introduction to Principal Curvatures and Curvature Tensor

This paragraph introduces the concept of using the curvature tensor to derive principal curvatures of a surface. It explains the process of finding the mean curvature by contracting the tensor's diagonal elements and calculating the Gaussian curvature through the determinant of the matrix. The paragraph also touches on the diagonalization of the matrix to find the principal curvatures, providing a formula for eigenvalues specific to a 2x2 matrix. The process is simplified for viewers without a background in linear algebra, focusing on the application of the formulas rather than their derivation.

05:01
🔍 Derivation of Principal Curvatures and Diagonalization

The second paragraph delves into the practical application of finding the principal curvatures by diagonalizing the curvature tensor. It demonstrates how to calculate the eigenvalues for a 2x2 matrix and use them to create a diagonal matrix with the same contraction and determinant values as the original. The paragraph clarifies that the diagonal elements of this new matrix represent the principal curvatures. It also discusses the geometric interpretation of diagonalization as a rotation of coordinate axes to eliminate off-diagonal elements, simplifying the understanding of curvature properties.

10:03
📐 Applying Curvature Tensor to Sample Surfaces

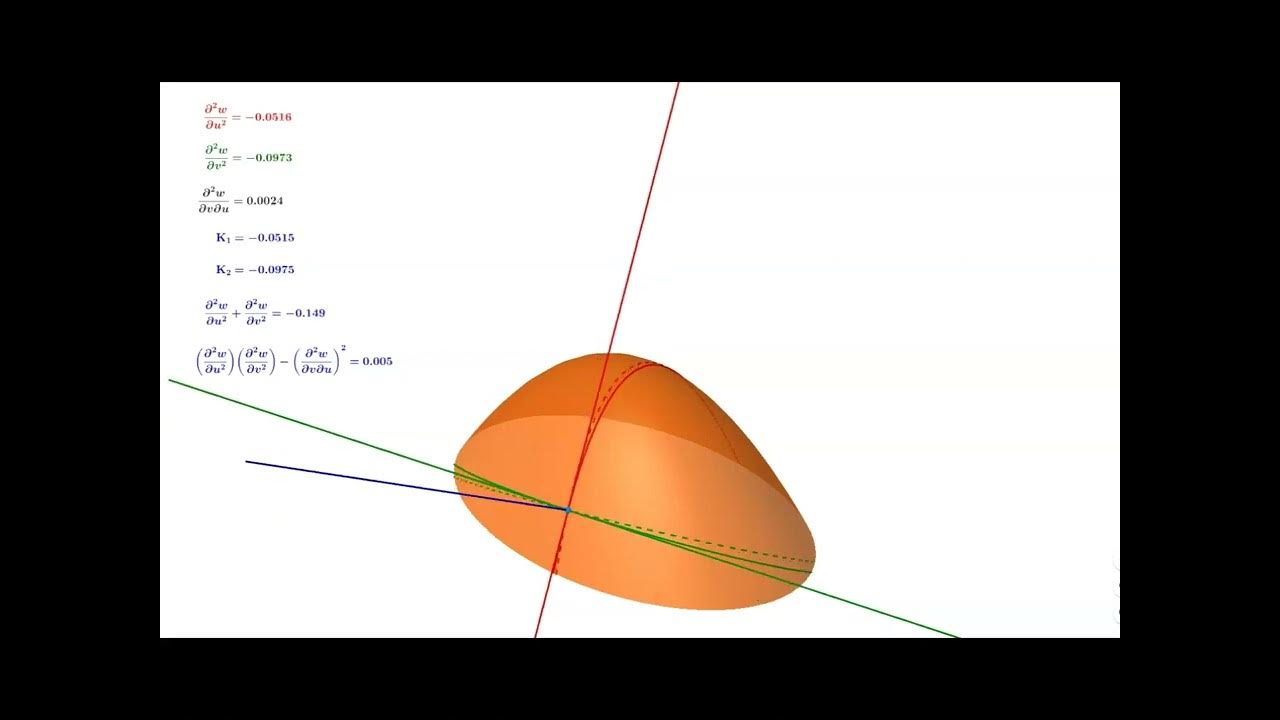
This paragraph applies the concepts discussed to analyze sample surfaces, such as a cylinder, a sphere, and a torus. It outlines the steps to raise the index of the curvature tensor using the contravariant metric tensor, form the contraction for mean curvature, calculate the determinant for Gaussian curvature, and identify the principal curvatures from the diagonal elements. The paragraph emphasizes the consistency of results obtained using the curvature tensor compared to traditional methods, highlighting the simplicity and directness of tensor calculus in analyzing curved surfaces.

15:04
🌐 Conclusion on the Utility of Tensor Calculus

The final paragraph concludes the discussion by summarizing the power and utility of tensor calculus in working with curved surfaces. It reiterates the ease with which tensor calculus allows for the calculation of invariant properties such as mean curvature, Gaussian curvature, and principal curvatures without the need for coordinate transformations or axis rotations. The paragraph leaves the viewer with an appreciation for the efficiency and comprehensiveness of tensor calculus in the context of differential geometry.

Mindmap
Keywords
💡Curvature Tensor
The curvature tensor is a mathematical object used in differential geometry to describe the curvature of a surface. In the context of the video, it is a 4x4 matrix with components that can be used to calculate various properties of a surface, such as mean curvature and Gaussian curvature. The script discusses how to derive the principal curvatures of a surface using the curvature tensor, which is central to understanding the intrinsic geometry of the surface.
💡Principal Curvatures
Principal curvatures are the eigenvalues of the shape operator or the second fundamental form of a surface. They provide a measure of the maximum and minimum curvature at a point on the surface. In the video, the process of finding these values involves diagonalizing the curvature tensor, which simplifies the calculation and reveals the principal curvatures as the eigenvalues of the matrix.
💡Mean Curvature
Mean curvature is a measure of the average curvature of a surface at a given point. It is defined as the trace of the shape operator or the sum of the principal curvatures. The script explains how to calculate the mean curvature by forming a contraction of the curvature tensor, which is the sum of the diagonal elements.
💡Gaussian Curvature
Gaussian curvature is a measure of the intrinsic curvature of a surface. It is defined as the determinant of the shape operator or the product of the principal curvatures. The video script discusses calculating Gaussian curvature by taking the determinant of the curvature tensor, which is the product of the diagonal elements minus the product of the off-diagonal elements.
💡Diagonalizing a Matrix
Diagonalizing a matrix is a process in linear algebra where a matrix is transformed into a diagonal form by finding its eigenvalues and eigenvectors. In the video, diagonalizing the curvature tensor is necessary to find the principal curvatures. The script mentions that this process involves using the eigenvalues to construct an equivalent matrix with only diagonal elements, which simplifies the analysis of the surface's curvature.
💡Eigenvalues
Eigenvalues are scalar values that characterize a linear transformation described by a matrix. In the context of the video, the eigenvalues of the curvature tensor are the principal curvatures of the surface. The script provides a formula for calculating the eigenvalues of a 2x2 matrix, which are then used to construct a diagonal matrix representing the curvature tensor.
💡Contravariant Metric Tensor
The contravariant metric tensor is a mathematical object used in differential geometry to raise or lower indices in tensor expressions. In the video, it is used to convert the components of the curvature tensor into a form where one index is upper (superscript) and the other is lower (subscript), which is necessary for calculating the contraction and determinant.
💡Tensor Contraction
Tensor contraction is an operation that involves summing the components of a tensor along one or more indices. In the video, contraction is used to calculate the mean curvature by summing the diagonal elements of the curvature tensor. This operation simplifies the tensor and allows for the extraction of scalar quantities from the tensor.
💡Determinant
The determinant is a scalar value that can be computed from the elements of a square matrix and provides important information about the matrix, such as whether it is invertible. In the context of the video, the determinant of the curvature tensor is used to find the Gaussian curvature, which is the product of the diagonal elements minus the product of the off-diagonal elements.
💡Sample Surfaces
Sample surfaces in the video are specific geometric shapes like a cylinder, a sphere, and a torus, which are used to illustrate the application of tensor calculus in calculating curvature properties. The script demonstrates how to derive the curvature tensor for each surface, calculate the mean and Gaussian curvatures, and identify the principal curvatures, providing concrete examples of the theoretical concepts discussed.
Highlights

Continuation of the discussion on using the curvature tensor to derive the principal curvatures of a surface.

Introduction of the curvature tensor formula and its relation to the mean curvature.

Explanation of the contraction process to find the mean curvature by summing the diagonal elements of the tensor.

Derivation of the Gaussian curvature through the determinant of the matrix with one upper and one lower index.

Clarification on the number of eigenvalues corresponding to the dimension of the matrix.

Presentation of the formula for finding eigenvalues of a 2x2 matrix.

Demonstration of the process to diagonalize a matrix using eigenvalues.

Calculation of the eigenvalues for the given curvature tensor example.

Formation of a diagonal matrix with eigenvalues to find the principal curvatures.

Comparison of the contraction and determinant of the diagonalized matrix to the original tensor.

Illustration of the process of rotating coordinate axes to achieve a diagonal matrix.

Application of the eigenvalue formula directly to find principal curvatures without matrix formation.

Reinforcement of the understanding that diagonal elements of a diagonal matrix equate to principal curvatures.

Demonstration of applying the learned concepts to a demo from previous videos.

Explanation of the correlation between individual elements of the curvature tensor and the components of the surface.

Application of the curvature tensor to derive invariant properties of sample surfaces like a cylinder, sphere, and torus.

Discussion on the intrinsic flatness of a cylinder and its zero Gaussian curvature.

Analysis of the curvature tensor for a sphere, highlighting uniform principal curvatures and Gaussian curvature.

Conclusion on the power and utility of tensor calculus in working with curved surfaces.

Transcripts

Browse More Related Video

Video 78 - Gaussian Curvature

Tensor Calculus Lecture 8c: The Curvature Tensor On The Sphere Of Radius R

Tensor Calculus Lecture 14c: Non-hypersurfaces - Relationship Among The Shift Tensors

Tensor Calculus Lecture 14f: Principal Curvatures

Tensor Calculus Lecture 14d: Non-hypersurfaces - Relationship Among Curvature Tensors 1

Video 75 - Sample Curvature Tensors

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Tensor CalculusCurvature TensorPrincipal CurvaturesMean CurvatureGaussian CurvatureSurface AnalysisLinear AlgebraEigenvaluesDiagonalizationGeometric Properties