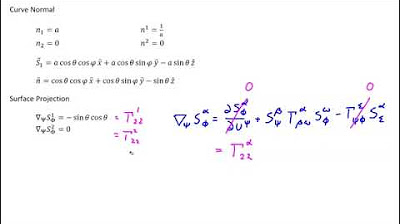Video 77 - Curvature Using Coordinate Systems
TLDRIn this 77th installment of the tensor calculus series, the video delves into quantifying the curvature of a line in space using a coordinate system. It simplifies the process by expressing the position vector in terms of a more convenient parameter and derives a general formula for curvature as a function of time. The script also explores the specific case of Cartesian coordinates and demonstrates how curvature can be visualized and calculated for a curve, especially when it's a single-valued function of x. The video concludes with a practical example and a visual demonstration of curvature, including the concept of radius of curvature and its implications.
Takeaways
- 📚 The video is part of a series on tensor calculus and focuses on quantifying the curvature of a line in space using a coordinate system.
- 🔍 It explains that finding an explicit relationship for arc length in terms of coordinate values is often impractical, so vectors are expressed in terms of a more convenient parameter.
- 📈 The video introduces the use of the chain rule to find the derivative of a position vector with respect to a parameter, resulting in a tangent vector to the curve.
- 📝 The goal is to derive an expression for curvature as a function of a parameter 't', rather than arc length 's', simplifying the notation with derivatives represented by a prime symbol.
- 🧩 The script walks through the algebraic process of finding the derivative of the position vector with respect to 't', leading to an expression for curvature.
- 📉 The curvature formula derived is applicable to any curve in two dimensions on a plane, using Cartesian coordinates, and simplifies the process of finding curvature.
- 📐 The video demonstrates how to calculate the curvature and radius of curvature for a curve, using the derived formula and the properties of derivatives.
- 🔢 If a curve can be represented as a single-valued function (y = f(x)), the curvature formula simplifies further, highlighting the relationship between curvature and the second derivative of the function.
- 📊 The script includes a visual demonstration of curvature, showing how it varies along a curve and the concept of radius of curvature graphically.
- 🚗 It uses an analogy of driving on a country road to explain the concept of curvature, relating it to the act of steering and the resulting circular path traced by the vehicle.
- 🛠️ The video suggests a method to simplify curvature calculations by constructing a coordinate system where the horizontal axis is tangent to the curve, making the curvature calculation straightforward.
Q & A
What is the main topic of the video?
-The main topic of the video is the curvature of a line in space, specifically discussing how to quantify curvature using a coordinate system.
Why is it impractical to use the arc length 's' as a parameter for curvature calculations?
-It is impractical because it is usually difficult or impossible to find an explicit relationship for arc length 's' in terms of coordinate values, which is necessary when applying a specific coordinate system.
What is the chain rule used for in this context?
-The chain rule is used to find the derivative of the position vector 'r' with respect to a parameter 't', when 'r' is a function of 's' and 's' is a function of 't'.
What is the significance of the derivative of the position vector with respect to 't'?
-The derivative of the position vector with respect to 't' gives a vector that is tangent to the curve, which is crucial for understanding the curve's direction and curvature.
How does the video simplify the notation for derivatives with respect to 't'?
-The video uses a prime symbol (') to represent derivatives with respect to 't', for example, the derivative of 'r' with respect to 't' is represented as 'r' primed (r').
What is the goal of the video in terms of curvature calculation?
-The goal is to derive an expression for curvature as a function of 't' instead of 's', making it easier to apply in various coordinate systems.
What is the relationship between the second derivative of 'r' with respect to 's' and curvature?
-The second derivative of 'r' with respect to 's' is used to find the curvature, as it provides information about how the direction of the tangent vector is changing along the curve.
How does the video approach the calculation of curvature in Cartesian coordinates?
-The video limits the example to a plane in Cartesian coordinates, where the position vector 'r' is expressed in terms of 'x' and 'y', and then calculates the necessary derivatives to find curvature.
What is the significance of 's prime' (ds/dt) in the curvature formula?
-'s prime' represents the rate of change of arc length 's' with respect to the parameter 't', and it is used in the denominator of the curvature formula to normalize the rate of change of direction.
How does the video demonstrate the concept of curvature visually?
-The video uses a graphical representation of a curve with a tangent line and a circle that is tangent to the curve and the tangent line, illustrating the curvature and radius of curvature at different points on the curve.
What special case is highlighted when the tangent of the curve is parallel to the x-axis?
-When the tangent of the curve is parallel to the x-axis, the curvature simplifies to just the second derivative of the function, as the slope term in the denominator of the curvature formula drops out.
How can a coordinate system be constructed to simplify curvature calculations?
-A coordinate system can be constructed where the horizontal axis is the tangent to the curve and the vertical axis is the radius, transforming the function to be a function of 'u' and 'v', which simplifies the curvature calculation to the second derivative with respect to 'u'.
Outlines
📚 Introducing Curvature Quantification with Coordinate Systems
This paragraph introduces the topic of quantifying the curvature of a line in space using a coordinate system. The script discusses the impracticality of using arc length for analytical purposes and the common approach of expressing the position vector 'r' as a function of a more convenient parameter for the chosen coordinate system. The paragraph also revisits the chain rule application from a previous video to find the derivative of 'r' with respect to a parameter 't', resulting in a tangent vector with a magnitude related to 's', the arc length parameter. The goal is to derive an expression for curvature as a function of 't', simplifying notation with the prime symbol for derivatives with respect to 't', and setting up the groundwork for further exploration.
🔍 Deriving Curvature as a Function of Parameter 't'
The focus shifts to deriving an expression for curvature in terms of the parameter 't'. The script explains the process of differentiating both sides of the derived equation with respect to 't', using the chain rule for the left side and standard differentiation rules for the right side. The result is an expression for curvature that is explicitly a function of 't', showcasing how all components are now related to 't' rather than 's'. This is a significant step as it allows for the analysis of curvature within the context of a specific coordinate system and parameterization.
📈 Applying Curvature Formula in Cartesian Coordinates
The script applies the derived curvature formula specifically to Cartesian coordinates in a two-dimensional plane. It simplifies the process by considering the position vector 'r' as a function of 't', with 'x' and 'y' as its components. The first and second derivatives of 'r' with respect to 't' are calculated, and 's' prime and 's' double prime are derived from the metric equation. The algebraic substitution of these values into the curvature formula yields a general expression for curvature in Cartesian coordinates. The magnitude of the resulting vector gives the scalar curvature, which is the main interest. The paragraph concludes with a simplified version of the formula for cases where the curve can be represented as a single-valued function of 'x'.
🌐 Visualizing Curvature and Its Implications
This paragraph discusses visualizing curvature through a demonstration using a third-degree polynomial function of 'x'. It explains how the curvature, represented by 'kappa', and the radius of curvature are calculated and their relationship to the function's derivatives. The script uses a graphical representation to illustrate how curvature changes at different points on the curve, with the radius of curvature decreasing at sharper turns and increasing along straighter sections. An analogy of driving on a country road is used to help conceptualize the idea of curvature. The paragraph also introduces the concept of constructing a coordinate system where the horizontal axis is tangent to the curve, simplifying the curvature calculation to the second derivative with respect to the new parameter 'u'. The section ends with a preview of upcoming discussions on the curvature of a surface.
Mindmap
Keywords
💡Tensor Calculus
💡Curvature
💡Coordinate System
💡Arc Length
💡Chain Rule
💡Tangent Vector
💡Metric Equation
💡Derivative
💡Cartesian Coordinates
💡Radius of Curvature
💡Inflection Point
Highlights
Introduction to the concept of quantifying the curvature of a line in space using a coordinate system.
The impracticality of finding an explicit relationship for arc length in terms of coordinate values.
The use of a parameter more convenient with the coordinate system to express vector r.
Derivation of the relationship between the derivative of position vector r and the tangent vector.
The simplification of notation using the prime symbol for derivatives with respect to t.
The derivation of dr/ds in terms of r' and s'.
The process of taking the derivative of both sides of the expression dr/ds with respect to t.
The final expression for curvature as a function of t, derived from the chain rule and metric equation.
Application of the curvature formula in Cartesian coordinates for a plane curve.
Explanation of how to find r' and r'' for a curve parameterized by t in Cartesian coordinates.
Derivation of s' and s'' using the metric equation for a curve in Cartesian coordinates.
The algebraic process of substituting expressions into the curvature formula.
The significance of the magnitude of the curvature vector in determining the actual curvature.
Special case of the curvature formula when the curve can be represented as a single-valued function of x.
The curvature at a point where the tangent to the curve is parallel to the x-axis simplifies to the second derivative.
Visual demonstration of curvature and radius of curvature with a third-degree polynomial function.
The concept of constructing a coordinate system where the horizontal axis is the tangent to the curve.
The upcoming discussion on the curvature of a surface in the next video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: