Let’s Solve These Basic Algebra Equations- Step-by-Step…….

TabletClass Math
25 Oct 202114:27
EducationalLearning
32 Likes 10 Comments

TLDRIn this instructional video, John, the founder of Tabit Class Math and a middle high school math teacher, introduces viewers to basic algebra equations. He emphasizes the importance of understanding one-step algebraic equations as a foundation for tackling more complex problems. John uses the concept of balance, akin to a teeter-totter, to explain how to maintain equality in an equation. He demonstrates solving for variables in four different scenarios involving addition, subtraction, multiplication, and division, highlighting the use of inverse operations. The video encourages practice and provides resources for further learning, aiming to build a strong algebraic foundation.

Takeaways
  • 📚 The video is aimed at teaching basic algebra equations, serving as a review for some and an introduction for others.
  • 👋 John, the founder of Tabit Class Math and a middle/high school math teacher, introduces himself and offers resources for math assistance.
  • 🔗 Links to John's math help program and pre-algebra notes are provided in the video description for further learning.
  • 📝 The script covers four types of one-step algebra problems: addition, subtraction, multiplication, and division.
  • ⚖️ Algebra equations are likened to a balanced scale, emphasizing the need to keep the equation in equilibrium by performing the same operations on both sides.
  • 🔢 The video explains the process of isolating the variable (x, y, t, z, etc.) on one side of the equation to solve for it.
  • 📉 For the equation x + 3 = -9, the solution involves subtracting 3 from both sides to isolate x, resulting in x = -12.
  • 📈 In the case of y - 2 = 10, adding 2 to both sides isolates y, leading to the solution y = 12.
  • 🎯 The concept of inverse operations is introduced: addition has subtraction as its inverse, and multiplication has division as its inverse.
  • 🆚 Solving -2t = 14 involves dividing both sides by -2 to isolate t, resulting in t = -7.
  • 🧩 The last problem with fractions (2/5 * h = 1/2) is solved by multiplying both sides by the reciprocal of 2/5, which is 5/2, to isolate h and find h = 5/4.
Q & A

  • What is the primary focus of the video script?

    -The primary focus of the video script is to teach basic algebra equations and the fundamental concepts required to solve them.

  • Who is John and what is his role in the video?

    -John is the founder of Tabit Class Math and a middle high school math teacher. He is the instructor in the video, guiding viewers through basic algebra problems.

  • What is the significance of maintaining balance in algebra equations?

    -Maintaining balance in algebra equations is crucial because it ensures that the equation remains valid and equal on both sides, which is essential for finding the correct solution.

  • What does John suggest viewers do if they think they know how to solve the problems?

    -John encourages viewers who think they know how to solve the problems to pause the video and attempt to solve the problems themselves to test their understanding.

  • What are the four types of basic algebra problems discussed in the video?

    -The four types of basic algebra problems discussed are addition, subtraction, multiplication, and division scenarios, often referred to as one-step equations.

  • How does John explain the concept of inverse operations in algebra?

    -John explains the concept of inverse operations by using the analogy of adding weight to one side of a scale and then adding an equal amount of weight to the other side to maintain balance. In algebra, the inverse operation is used to cancel out an operation on one side of the equation, ensuring the equation remains balanced.

  • What is the main rule of solving algebra equations according to John?

    -The main rule of solving algebra equations, as explained by John, is that whatever operation you perform on one side of the equation, you must perform the exact same operation on the other side to maintain balance.

  • How does John approach solving the multiplication problem involving 'negative 2 times t equals 14'?

    -John approaches the multiplication problem by dividing both sides of the equation by negative two, which is the inverse operation of multiplication, to isolate the variable t.

  • What technique does John use to solve the division problem involving fractions?

    -John uses the technique of multiplying both sides of the equation by the reciprocal of the fraction in front of the variable to solve the division problem.

  • Why does John emphasize the importance of practice in learning algebra?

    -John emphasizes the importance of practice because it is the only way to solidify understanding and gain proficiency in solving algebra problems, especially as one progresses to more complex equations.

  • What resources does John offer for those who need additional math help?

    -John offers his math help program for a comprehensive learning experience and suggests his YouTube channel for a variety of solved problems and teaching styles.

Outlines
00:00
📚 Introduction to Basic Algebra Equations

The speaker, John, founder of Tabit Class Math and a middle/high school math teacher, introduces the video's purpose: teaching basic algebra equations. He emphasizes that mastering these fundamentals is crucial before moving on to more advanced topics. John encourages viewers to practice along with the video to solidify their understanding. He also promotes his online math classes and pre-algebra notes for additional help, providing links in the video description. The video will cover four types of one-step algebraic problems: addition, subtraction, multiplication, and division.

05:01
🔍 Understanding Algebraic Balance and Operations

John explains the concept of maintaining balance in algebraic equations, using the analogy of a teeter-totter. He stresses that any operation performed on one side of the equation must be mirrored on the other side to keep the equation balanced. The video demonstrates how to isolate variables by performing inverse operations, such as subtracting to counteract addition or dividing to counteract multiplication. John solves several one-step equations, illustrating the process of eliminating constants and coefficients to solve for the variable.

10:01
📘 Applying Inverse Operations to Algebraic Problems

Continuing the lesson, John applies the concept of inverse operations to solve algebraic equations. He shows how to deal with negative numbers and how to use addition or subtraction to balance the equation. The video progresses to multiplication and division scenarios, where John demonstrates dividing both sides of an equation by a number to isolate the variable. He simplifies the process of dealing with fractions by multiplying both sides by the reciprocal of the fraction, effectively canceling it out and solving for the variable.

🎓 Embracing Practice and Moving Beyond Basic Algebra

In the concluding part of the video, John emphasizes the importance of practice in mastering algebra. He likens learning algebra to climbing a ladder, where each step represents a fundamental operation that must be understood before tackling more complex problems. John encourages viewers to utilize his math help program and YouTube channel for further practice and examples. He invites viewers to subscribe to his channel and like the video if they found it helpful, wishing them success in their mathematical journey.

Mindmap
Keywords
💡Algebra
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating those symbols. It is a unifying thread of almost all of mathematics and includes everything from solving elementary equations to the study of abstractions such as groups, rings, and fields. In the context of the video, algebra refers to the process of solving equations using basic mathematical operations. The video script emphasizes the importance of understanding algebra as a fundamental step to solving more complex equations.
💡One-step equations
One-step equations are algebraic equations that can be solved with a single operation, such as addition, subtraction, multiplication, or division. They are typically introduced to students as a way to understand the basic principles of algebra before moving on to more complex equations. In the video, one-step equations serve as the primary focus, with the instructor demonstrating how to solve them using basic algebraic principles.
💡Positive and negative numbers
Positive and negative numbers are used to represent quantities with opposite effects, such as temperatures above and below zero or moving forward and backward. In algebra, understanding how to work with these numbers is crucial for solving equations. The script mentions that if viewers are not familiar with positive and negative numbers, they should refer to other resources provided by the instructor.
💡Equation balance
Equation balance refers to the property that both sides of an equation must remain equal after any operation is performed on one side. This concept is analogous to a physical balance or scale, where adding or removing weight on one side necessitates a corresponding change on the other side to maintain equilibrium. The video script uses the analogy of a teeter-totter to explain the importance of keeping the equation balanced when solving for variables.
💡Variable
In algebra, a variable is a symbol, usually a letter, that stands for an unknown number or value. Variables are used to represent elements in a mathematical expression or to denote unknowns in an equation. The script discusses the goal of isolating the variable on one side of the equation to solve for its value.
💡Inverse operations
Inverse operations are mathematical operations that 'undo' or reverse the effect of another operation. For example, the inverse of multiplication is division, and the inverse of addition is subtraction. The video script explains how to use inverse operations to solve one-step equations, such as dividing both sides of an equation by a number to isolate the variable.
💡Multiplication
Multiplication is one of the four basic arithmetic operations, where two numbers are combined to give a product. In the context of the video, multiplication is used in equations, and the instructor demonstrates how to solve for a variable when it is multiplied by a number by using division.
💡Division
Division is the arithmetic operation of splitting a number into equal parts or groups. In algebra, division is often used to isolate a variable in an equation. The script shows how division can be applied to both sides of an equation to cancel out a coefficient in front of a variable.
💡Reciprocal
A reciprocal is a number which, when multiplied by the original number, results in a product of one. In the context of the video, the reciprocal is used to eliminate a fraction in front of a variable by multiplying both sides of the equation by the reciprocal of the fraction, thus isolating the variable.
💡Practice
Practice refers to the act of repeatedly performing an activity or set of activities to improve one's skill or understanding. In the video, the instructor emphasizes the importance of practice in mastering algebra, suggesting that viewers should engage in solving numerous problems to become proficient.
Highlights

Introduction to basic algebra equations and the importance of understanding them before tackling advanced problems.

Encouragement for viewers to pause the video and attempt solving the problems independently as a form of practice.

Introduction of John, the founder of Tabit Class Math, and his experience as a middle high school math teacher.

Mention of online math classes and resources available for those needing math assistance, including a link in the video description.

Overview of the four types of basic algebra problems to be covered: addition, subtraction, multiplication, and division.

Explanation of the concept of balance in algebra, comparing it to a teeter-totter to illustrate the need for maintaining equation equilibrium.

Rule of algebra emphasized: whatever operation is performed on one side of the equation must be equally performed on the other side.

Demonstration of solving the first problem, x plus 3 equals negative 9, using the concept of inverse operations.

Solving the second problem, y minus 2 equals 10, by applying the same technique of inverse operations.

Introduction to the concept of inverse operations in algebra: addition's inverse is subtraction, and multiplication's inverse is division.

Solution to the multiplication problem, negative 2 times t equals 14, using division to isolate the variable.

Approach to solving the division problem involving fractions, by multiplying both sides by the reciprocal of the fraction.

Emphasis on the importance of understanding and practicing fraction problems and working with positive and negative numbers.

Comparison of solving basic equations to climbing stairs, where each step represents a fundamental operation in algebra.

Advice on the necessity of practice for mastering algebra, suggesting the use of the math help program and YouTube channel for additional practice.

Invitation for viewers to subscribe to the channel for regular math content and to like the video if they found it helpful.

Transcripts

Browse More Related Video

Algebraic Equations and Their Solutions

Algebra SYSTEM WORD PROBLEM – Let’s solve it step-by-step...

Math Videos: How To Learn Basic Arithmetic Fast - Online Tutorial Lessons

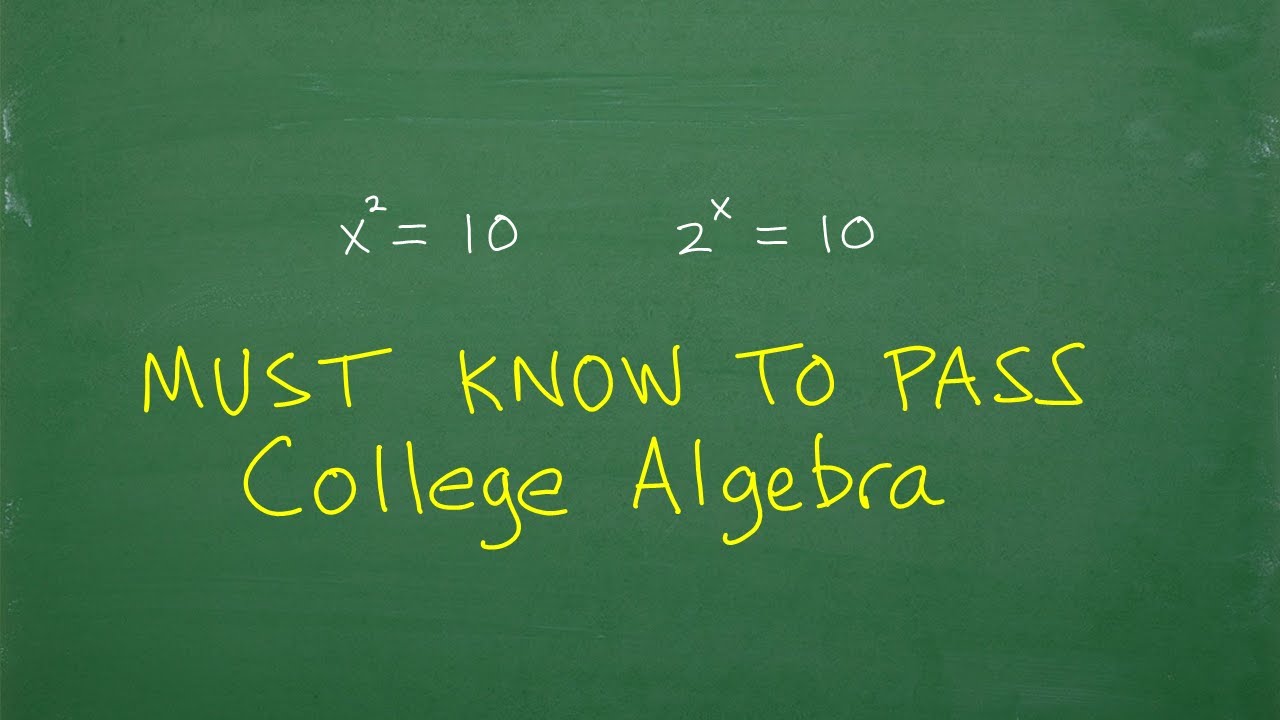
Want to PASS College Algebra? Absolutely, better understand this…

6 to the (3x + 5) = 1, many don’t know where to start

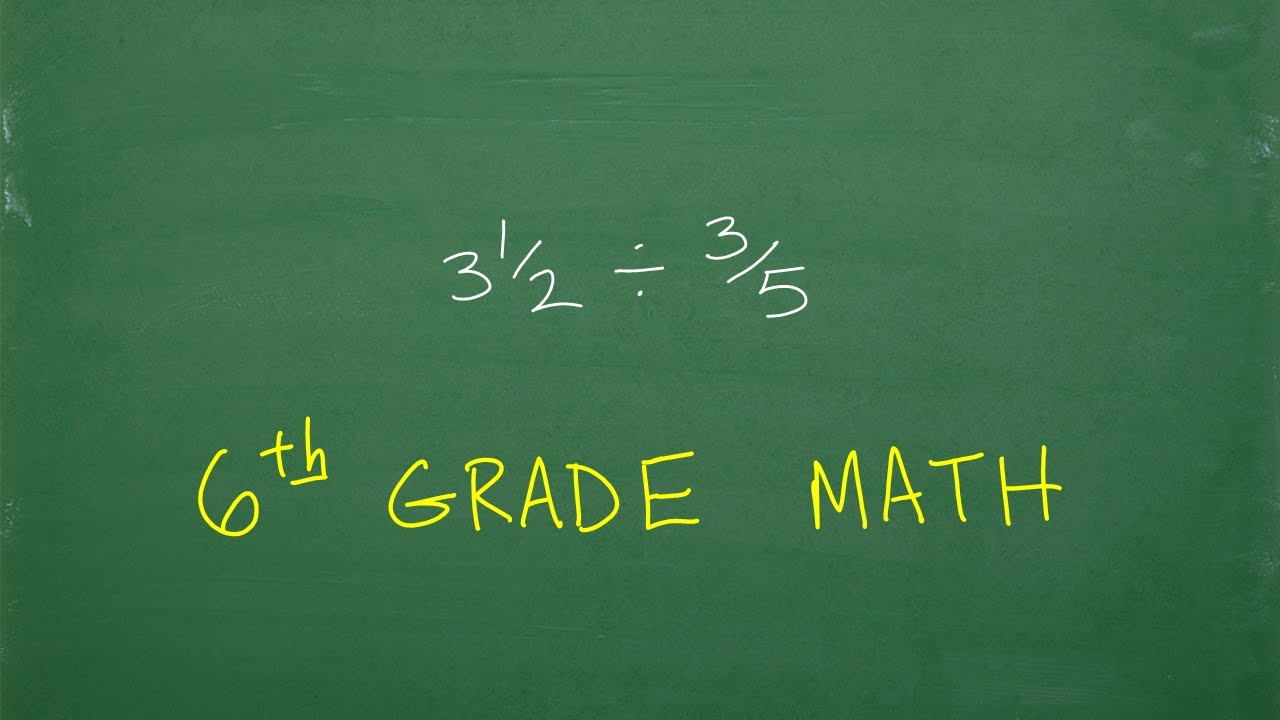
How to Divide Fractions – 6th Grade Math

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Algebra BasicsMath EducationEquation SolvingMiddle SchoolOnline ClassesMath TeacherEducational VideoTeeter Totter AnalogyInverse OperationsPractice Problems