Tensor Calculus 8: Covector Field Transformation Rules (Covariance)

eigenchris

5 Jun 201813:24

EducationalLearning

32 Likes 10 Comments

TLDRThis video delves into the transformation rules for differential forms, also known as covector fields, building upon concepts from the 'Tensors for Beginners' series. It explains how covector fields can be expanded into linear combinations of basis covector fields, which follow the contravariant transformation rule. The video also covers how covector field components transform using the covariant rule, utilizing the Jacobian and inverse Jacobian matrices. Through concrete examples, it confirms the covariant transformation law for covector components, providing a comprehensive understanding of vector and covector fields in calculus.

Takeaways

📚 The video discusses the transformation rules for differential forms, also known as covector fields, and serves as an advanced version of a previous video for beginners.
🔄 The video builds upon the understanding of covariant and contravariant transformation rules for vectors and covectors, which are essential in tensor calculus.
📉 The covector fields can be expanded into linear combinations of basis covector fields, and the transformation of these basis fields is explained in the video.
🔠 The script explains that basis covector fields follow the contravariant transformation rule, while covector field components follow the covariant rule.
🧭 The transformation from Cartesian to polar coordinates and vice versa for covector fields is demonstrated using the Jacobian and inverse Jacobian matrices.
📏 The video uses Einstein notation to summarize the transformation rules, which is a compact way to express tensor operations.
📐 The script provides a detailed explanation of how to check the orientation of covector fields in different coordinate systems, such as Cartesian and polar.
🔢 The video includes concrete examples to illustrate the covariant transformation law for covector components, using the chain rule from multivariable calculus.
🔄 The transformation between covector field components in Cartesian and polar coordinates is confirmed through matrix multiplication with the Jacobian and inverse Jacobian matrices.
📚 The video concludes by summarizing the transformation rules for both basis covector fields and their components, reinforcing the understanding of covariant and contravariant behavior.
🚀 The final takeaway is that the video sets the stage for further exploration of the link between the covector field interpretation of differentials and their role in integrals in the next video.

Q & A

What are differential forms also known as?
-Differential forms are also known as covector fields.
What is the relationship between the covariant transformation rule and the contravariant transformation rule?
-The covariant transformation rule is the opposite of the contravariant transformation rule. While covariant transformation is used to go from the old basis to the new basis, the contravariant transformation is used to go from new components to old components and vice versa.
How do we expand a covector field in terms of basis covector fields?
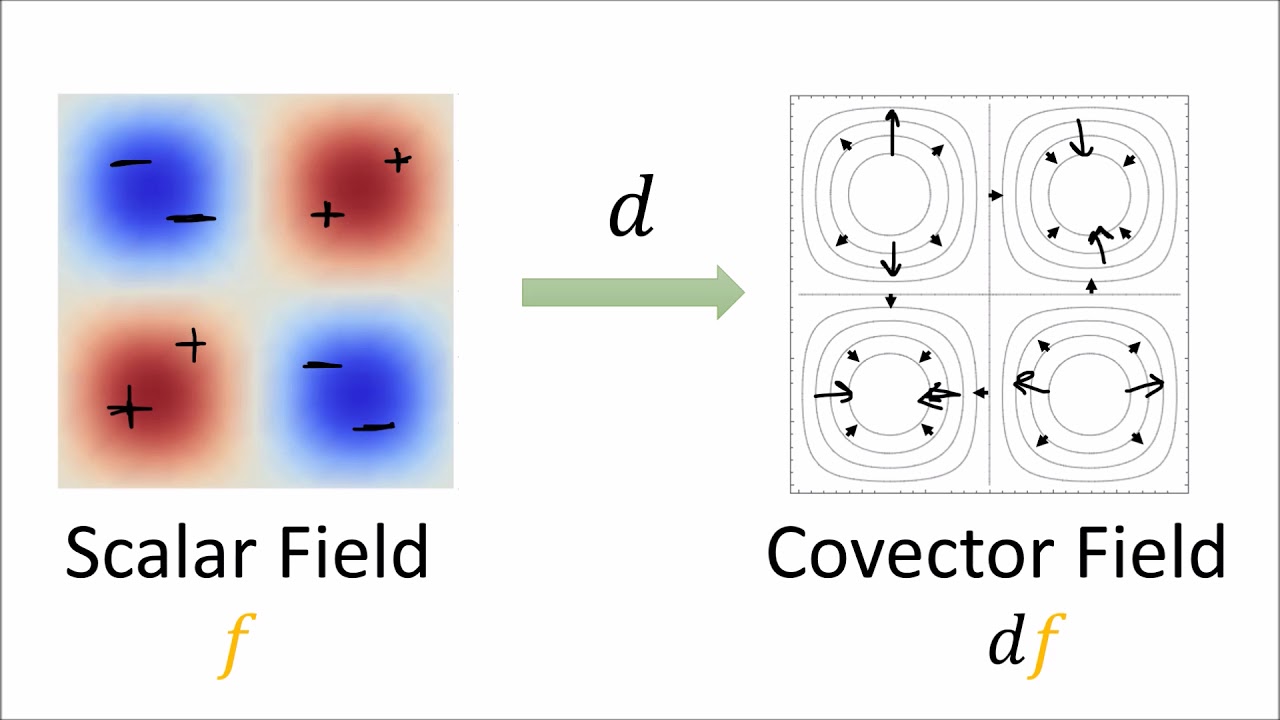
-A covector field can be expanded into linear combinations of basis covector fields. For instance, any covector field DF can be expressed as a linear combination of dX and dy.
What is the role of the Jacobian matrix in transforming covector fields?
-The Jacobian matrix is used for the forward transformation (from old to new basis), and its inverse is used for the backward transformation (from new to old basis) in the context of covector field components.
Why do covector field components obey the covariant transformation rule?
-Covector field components obey the covariant transformation rule because they vary in the same way as basis vectors do. When basis vectors grow, covector components also grow, indicating their covariant nature.
What does the orientation of the covector field dr imply along the x-axis?
-Along the x-axis, the orientation of the covector field dr points outward. When x is positive, it points to the right, and when x is negative, it reverses the direction but still points to the right due to the orientation of the curves.
How can the transformation rules for basis covector fields be summarized using Einstein notation?
-The transformation rules for basis covector fields can be summarized in Einstein notation by expressing the relationship between the old and new basis covector fields using the inverse Jacobian matrix for the contravariant transformation.
What is the significance of using matrix notation when expressing the transformation of covector fields?
-Matrix notation provides a concise and systematic way to express the transformation of covector fields. It clearly shows how the basis covector fields and their components transform between different coordinate systems using the Jacobian and its inverse.
Can you provide an example of how to apply the covariant transformation rule for covector components?
-An example would be converting the components of a covector field from Cartesian coordinates to polar coordinates using the Jacobian matrix. The covector components are placed in a row vector and multiplied by the Jacobian matrix to obtain the components in the new coordinate system.
How is the multivariable chain rule used to convert between covector field components in different coordinate systems?
-The multivariable chain rule is used to find the relationships between partial derivatives in different coordinate systems. By applying the chain rule, one can convert covector field components from one set of coordinates to another, adhering to the covariant transformation rule.

Outlines

00:00

📚 Introduction to Differential Forms Transformation

This paragraph introduces the topic of the video, which is the transformation rules for differential forms, also known as covector fields. It sets the stage by referencing a previous video on tensors for beginners and suggests that viewers watch it for better understanding. The paragraph explains the concepts of expanding vectors and covectors into linear combinations of basis vectors and covector fields, and how these expansions are affected by different transformation rules, such as covariant and contravariant transformations. It also mentions the importance of understanding how basis covector fields and their components transform, which will be the focus of the video.

05:02

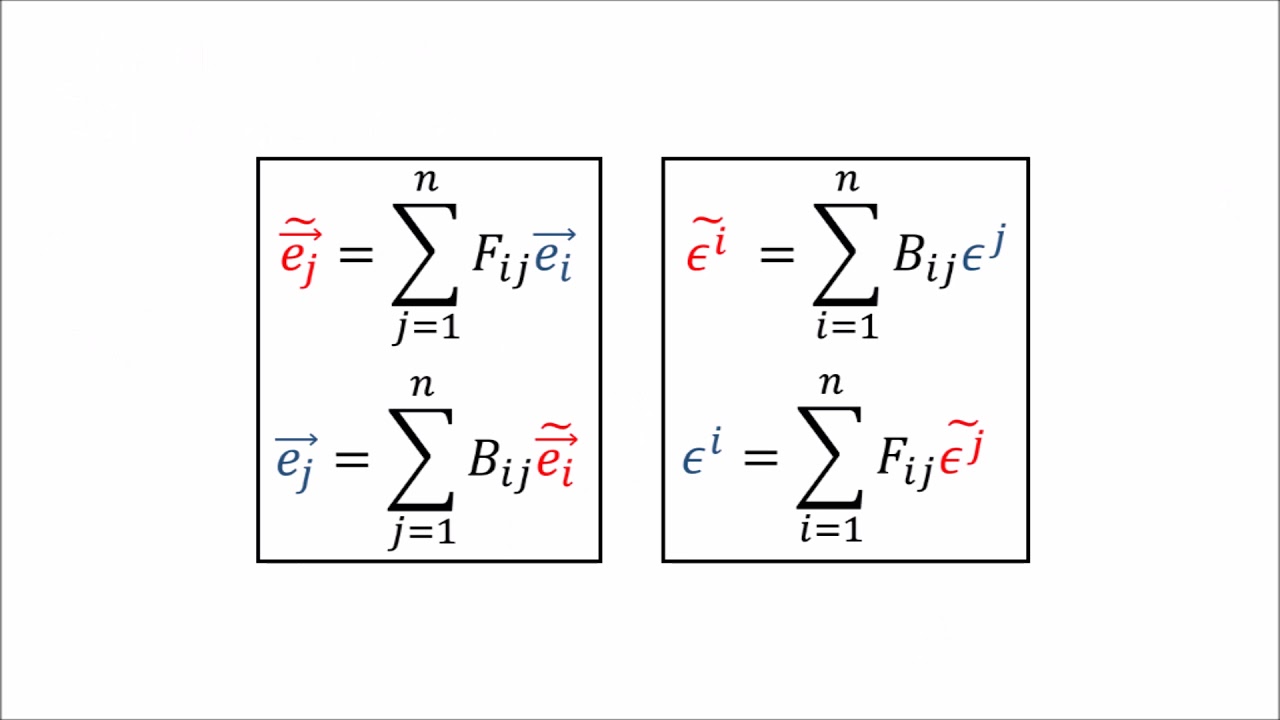
🔍 Contravariant Transformation of Basis Covector Fields

The second paragraph delves into the transformation rules for basis covector fields, emphasizing the contravariant transformation rule. It explains how any covector field can be expressed as a linear combination of basis covector fields, using the inverse Jacobian matrix as coefficients. The paragraph also discusses the orientation of the covector fields in Cartesian and polar coordinates, ensuring that the transformation rules make sense in different coordinate systems. The contravariant transformation is summarized using Einstein notation and matrix notation, highlighting the use of the inverse Jacobian matrix for transformations from old to new basis.

10:05

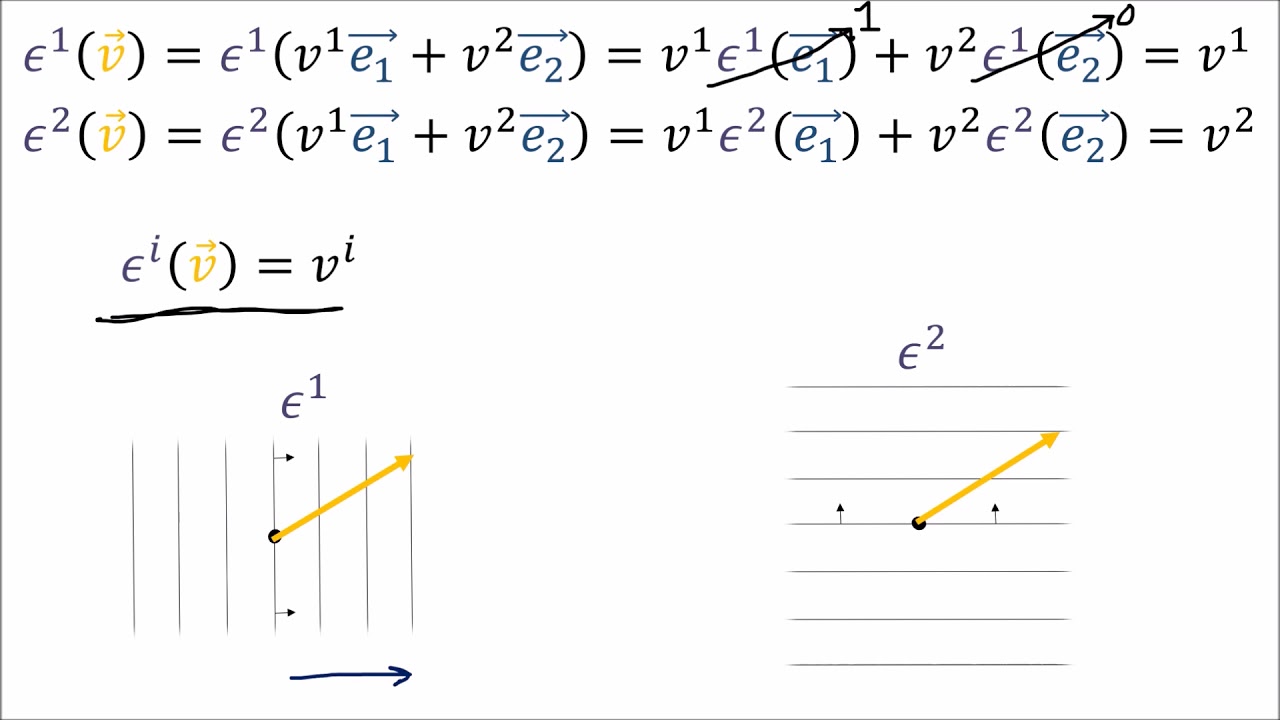
🔄 Covariant Transformation of Covector Field Components

This paragraph explores the covariant transformation of covector field components, contrasting it with the contravariant transformation of basis covector fields. It uses the multivariable chain rule to convert between Cartesian and polar components of a covector field, demonstrating the covariant nature of these components. The paragraph provides a concrete example of a scalar field and its corresponding covector field components in both coordinate systems, confirming the covariant transformation rule through matrix multiplication with the Jacobian matrix for transformations from old to new components and the inverse Jacobian for the reverse.

📘 Conclusion and Future Outlook

The final paragraph wraps up the discussion on the transformation rules for both basis covector fields and their components. It confirms the understanding of the covariant transformation rule for covector field components through concrete examples and matrix operations. The paragraph also hints at the next step in the series, which will involve linking the covector field interpretation of differentials, such as 'dX', with their differential interpretation in integrals, by reinterpreting the concept of integration.

Mindmap

Keywords

💡Differential Forms

Differential forms, also known as covector fields, are mathematical objects used in the field of differential geometry and calculus to generalize the concept of differentials and integrate over manifolds. In the video, differential forms are the main focus, as they discuss the transformation rules for these forms, which are crucial for understanding how they behave under changes of coordinates.

💡Covector Fields

Covector fields are a type of differential form that can be thought of as a linear functional on the space of smooth vector fields. They are dual to the notion of a vector field and are used to define differential operators such as the exterior derivative. The script explains how these fields transform under different coordinate systems, which is a key aspect of their behavior in differential geometry.

💡Transformation Rules

Transformation rules describe how mathematical objects change when switching between different coordinate systems. In the context of the video, the transformation rules for differential forms are discussed, which include both covariant and contravariant transformations. These rules are essential for understanding how differential forms behave when the basis vectors change.

💡Covariant Transformation

A covariant transformation is a rule that describes how the components of a tensor or a covector field change under a change of coordinates. In the video, it is explained that basis covector fields obey the contravariant transformation rule, while covector components obey the covariant transformation rule, which is a fundamental concept in tensor calculus.

💡Contravariant Transformation

Contravariant transformation is the opposite of covariant transformation, where the components of a vector or a covector field change in the opposite way to the change in basis. The video script provides an example of how covector fields can be expanded into linear combinations of basis covector fields using the contravariant transformation rule.

💡Basis Vectors

Basis vectors are the fundamental vectors in a vector space that can be used to express any vector in that space as a linear combination of the basis vectors. In the script, basis vectors are discussed in the context of their transformation rules and how they relate to the expansion of vector fields and covector fields.

💡Jacobian Matrix

The Jacobian matrix is a matrix of all first-order partial derivatives of a vector-valued function. It is used to describe how a function transforms when changing variables. In the video, the Jacobian matrix is used to express the transformation rules for covector fields and to show how components of these fields change from one coordinate system to another.

💡Inverse Jacobian Matrix

The inverse Jacobian matrix is the matrix that, when multiplied by the Jacobian matrix, yields the identity matrix. It represents the transformation from the new basis to the old basis. In the script, the inverse Jacobian matrix is used to describe the backward transformation of covector fields.

💡Multivariable Chain Rule

The multivariable chain rule is a generalization of the chain rule for functions of multiple variables. It is used to compute derivatives of composite functions involving multiple variables. In the video, the chain rule is used to explain how to convert between covector field components in different coordinate systems.

💡Einstein Notation

Einstein notation, also known as Einstein summation convention, is a notational convention used in physics and mathematics to simplify the writing of equations involving sums. In the script, Einstein notation is used to succinctly express the transformation rules for covector fields and their components.

💡Scalar Field

A scalar field is a function that assigns a scalar value to every point in space. It is used in the video to illustrate the concept of covector fields and how they can be represented in different coordinate systems. The script provides an example of a scalar field defined in both Cartesian and polar coordinates.

Highlights

Introduction to transformation rules for differential forms, also known as covector fields.

Connection to the covector transformation rules from the 'Tensors for Beginners' series.

Explanation of vector expansion in linear combinations of basis vectors and the covariant transformation rule.

Contrasting the contravariant transformation rule with the covariant rule in vector components.

Differential forms can be expanded into linear combinations of basis covector fields.

The inverse Jacobian matrix as coefficients in the expansion of covector fields in Cartesian coordinates.

Contravariant transformation rule for covector fields as demonstrated through the inverse Jacobian.

Matrix notation for expressing the transformation of covector fields.

Verification of covector field transformation formulas using specific orientations on the coordinate axes.

Building Cartesian basis covector fields from polar basis covector fields using the Jacobian matrix.

Covector field components transformation rules using the covariant transformation rule.

The multivariable chain rule for converting between covector field components in different coordinate systems.

Covector components' covariance demonstrated through the relationship with basis vectors.

Concrete examples of covariant transformation law for covector components with scalar field F.

Confirmation of covariant transformation rule correctness through matrix multiplication and variable substitution.

Summary of transformation rules for basis covector fields and covector field components.

Upcoming exploration of the link between covector field interpretation and differential interpretation in integrals.

Transcripts

Browse More Related Video

Tensors for Beginners 6: Covector Transformation Rules

Tensors for Beginners 12: Bilinear Forms are Covector-Covector pairs

Tensor Calculus 6: Differential Forms are Covectors

Tensors for Beginners 5: Covector Components (Contains diagram error; see description)

Tensor Calculus 5: Derivative Transformation Rules (Contravariance)

Tensor Calculus 10: Integration with Differential Forms Examples