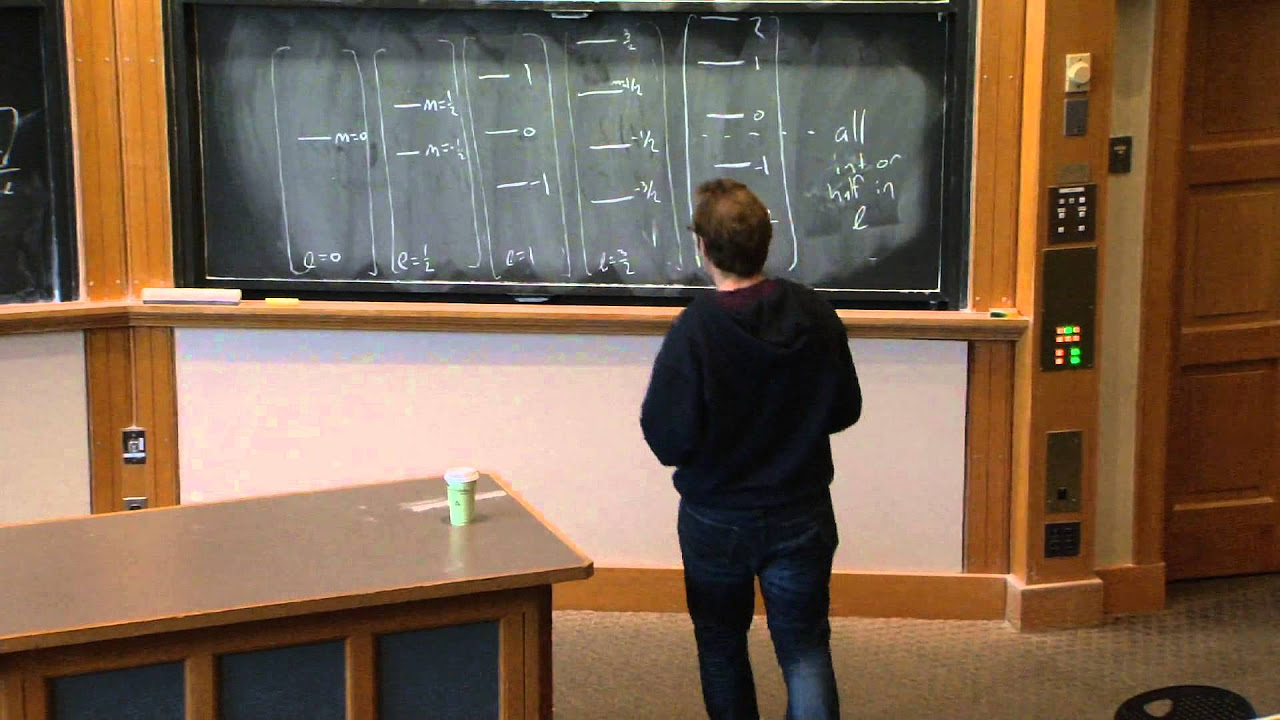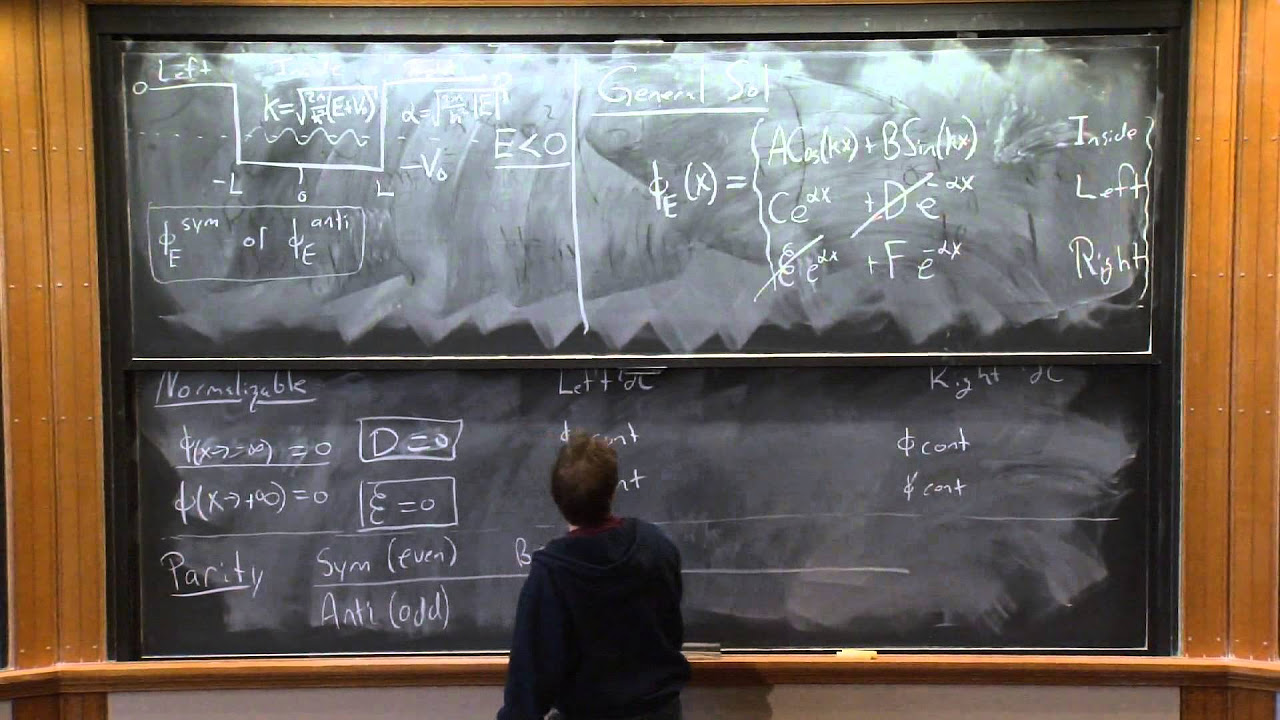Lecture 17: More on Central Potentials
TLDRThis lecture delves into the quantum mechanical properties of particles, particularly focusing on angular momentum and its implications for systems like the hydrogen atom. The professor discusses the peculiarities of half-integer spin states, the Stern-Gerlach experiment, and the concept of intrinsic angular momentum or 'spin'. The lecture also covers the mathematical formulation of the Laplacian in spherical coordinates and explores the solutions to the energy eigenvalue equation for central potentials, providing insights into the stability and energy levels of systems like the spherical well and the hydrogen atom.
Takeaways
- 📚 The lecture discusses the peculiarities of half-integer states in quantum mechanics, particularly focusing on the impossibility of representing these states with a probability distribution on a sphere due to their wave functions equating to minus themselves upon a 2π rotation.
- 🧲 The professor uses the example of a magnet in a magnetic field gradient to explain how angular momentum can be measured through the deflection of a magnetic object, which is related to the Stern-Gerlach experiment that reveals the quantization of angular momentum.
- 🔬 The Stern-Gerlach experiment is highlighted as a key discovery that electrons exhibit a form of angular momentum (spin) with discrete values, challenging classical notions of rotation and leading to the concept of intrinsic angular momentum or 'spin'.
- 🌀 The lecture introduces the Laplacian in three dimensions, specifically in spherical coordinates, and discusses its significance in solving problems related to central potentials and spherically symmetric systems.
- 📉 The importance of the commutation relations of angular momentum operators is underscored, as they lead to the quantization of angular momentum and the understanding of half-integer states.
- 💡 The concept of 'effective potential' is introduced, which includes contributions from the original potential and the centrifugal barrier due to angular momentum, crucial for solving the energy eigenvalue equation in spherical coordinates.
- 🚀 The lecture demonstrates the use of separation of variables to simplify the energy eigenvalue equation into a one-dimensional form, applicable to central potentials, and discusses the implications of this simplification.
- 🔍 The professor emphasizes the importance of boundary conditions for wave functions in central potentials, particularly the requirement for wave functions to vanish at the origin due to physical constraints.
- 🔑 The energy eigenvalue equation for central potentials is shown to be dependent on the quantum number 'l' but not 'm', revealing a degeneracy in energy levels that is a direct consequence of rotational symmetry.
- 🌐 The lecture touches on the implications of rotational symmetry in quantum systems, explaining how it leads to energy level degeneracies and the existence of a common eigenbasis for different components of angular momentum.
- 🚧 The professor builds a 'toy model' for the hydrogen atom using the Coulomb potential, emphasizing that while it is a good approximation, it is not an exact representation of hydrogen due to simplifications and assumptions made.
Q & A
What is the significance of the half integer states (l states) in quantum mechanics?
-The half integer states, particularly l = 1/2, represent intrinsic angular momentum or spin in quantum mechanics. These states cannot be represented by a probability distribution on a sphere due to their inherent properties that make the wave function equal to minus itself upon a 2π rotation, which is not physically plausible for a probability distribution.
Why can't half integer states be represented by a wave function on a sphere?
-Half integer states cannot be represented by a wave function on a sphere because doing so would require the wave function to be equal to minus itself at any given point after a 2π rotation, which contradicts the requirement that the wave function must be equal to itself at the same point, implying it must be zero, an impossibility for a probability distribution.
What is the relationship between angular momentum and magnetic moment in a rotating charged sphere?
-In a rotating charged sphere, the magnetic moment is proportional to the angular momentum. This relationship is derived from the right-hand rule, which indicates that a rotating charge distribution generates a magnetic field along the axis of rotation, and the strength of this magnetic moment is related to the amount of angular momentum.
How does the Stern-Gerlach experiment demonstrate the quantization of angular momentum?
-The Stern-Gerlach experiment demonstrates the quantization of angular momentum by sending particles, like electrons, through a magnetic field gradient. The deflection of the particles is measured, and it is found that they either deflect up or down by a fixed amount, indicating that the angular momentum can only take one of two possible values, which are quantized.
What is the significance of the Laplacian in spherical coordinates in the context of 3D quantum systems?
-The Laplacian in spherical coordinates is significant in 3D quantum systems as it simplifies the expression for the kinetic energy part of the Hamiltonian. It allows for the separation of variables in systems with spherical symmetry, making it easier to solve the Schrödinger equation for eigenfunctions and eigenvalues.
Why is it useful to express the energy operator in terms of eigenfunctions of L² (angular momentum squared) when dealing with central potentials?
-Expressing the energy operator in terms of eigenfunctions of L² simplifies the Schrödinger equation for systems with central potentials. Since the energy operator commutes with L², common eigenfunctions can be found, reducing the complexity of the problem and allowing for separation of variables, which leads to a more manageable radial equation.
What is the role of the effective potential in the Schrödinger equation for a system with a central potential?
-The effective potential in the Schrödinger equation for a system with a central potential accounts for both the original potential and the contribution from the angular momentum term. It modifies the original potential by adding a term that becomes significant at small radii due to the 1/r² dependence, which is a result of the conservation of angular momentum.
How does the change of variables from φ(r) to u(r) = rφ(r) simplify the Schrödinger equation for a central potential?
-The change of variables from φ(r) to u(r) = rφ(r) simplifies the Schrödinger equation by eliminating the 1/r and 1/r² terms that arise from the angular part of the Laplacian. This transformation results in a Schrödinger-like equation for u(r) that has the form of a one-dimensional problem with an effective potential, making it easier to solve.
What is the physical interpretation of the term h²/(2mr²)l(l+1) in the effective potential?
-The term h²/(2mr²)l(l+1) in the effective potential represents the kinetic energy contribution due to the angular momentum of the system. As the system approaches the origin with a fixed angular momentum, the kinetic energy, and hence the effective potential, increases, creating a barrier that prevents the particle from collapsing into the origin.
What are the conditions for the wave function near the origin (r = 0) in a system with a central potential?
-Near the origin, the wave function in a system with a central potential must be such that its kinetic energy does not diverge. This implies that the radial part of the wave function, u(r), must go to zero as r approaches zero to prevent the wave function from diverging, as the probability density is given by the square of the wave function, which includes a 1/r factor from the spherical harmonics.
Outlines
📚 Introduction to MIT OpenCourseWare and Quantum Angular Momentum
The script begins with an introduction to MIT OpenCourseWare, highlighting its mission to provide free, high-quality educational resources under a Creative Commons License. The professor then invites questions about angular momentum from previous lectures, leading to a detailed discussion on the peculiarities of half-integer spin states. These states, which cannot be represented by a wave function on a sphere, are previewed to be discussed in detail later in the course. The professor uses the analogy of a tiny bar magnet in a magnetic field gradient to hint at the intrinsic angular momentum of particles like electrons, setting the stage for a deeper exploration of quantum mechanics.
🧲 Magnetic Moment and Angular Momentum of Charged Particles
The professor delves into the relationship between angular momentum and magnetic moment, using the example of a charged sphere to explain how rotation generates a magnetic field. This concept is applied to the Stern Gerlach experiment, which measures the angular momentum of electrons by observing their deflection in a magnetic field gradient. The experiment reveals that electrons exhibit a quantized angular momentum, taking only specific values, and challenges classical notions of rotation. The discussion introduces the concept of 'spin' as an intrinsic form of angular momentum for particles like electrons, which is distinct from classical rotational angular momentum.
🌀 The Discovery of Quantum Angular Momentum
This section explores the historical context of the discovery of quantum angular momentum. The professor clarifies that the mathematical prediction of half-integer states preceded their physical understanding and experimental confirmation. The audience is reminded that the commutation relations leading to these states were observed mathematically before their physical significance was realized. The discussion also touches on the experimental observation of angular momentum being confined to specific values, leading to the concept of spin.
📘 Transition to 3D Quantum Systems and Spherical Coordinates
The script transitions into a discussion of three-dimensional quantum systems, with a focus on spherical coordinates. The professor introduces the Laplacian in spherical coordinates and highlights its significance in solving central potentials. The Laplacian is broken down into radial and angular components, with the angular component related to the square of the angular momentum operator. The section sets the stage for solving problems in 3D, including the exploration of spherically symmetric systems like the hydrogen atom.
🔍 Separation of Variables and Energy Eigenvalue Equation
The professor discusses the method of separation of variables to simplify the energy eigenvalue equation for a central potential. By recognizing that the energy operator and the angular momentum squared commute, the professor shows that it's possible to find common eigenfunctions for both. This leads to a simplification where the energy eigenvalue equation becomes a one-dimensional problem for the radial part of the wave function, with the angular part contributing a constant to the effective potential.
🌐 Effective Potential and Wave Function Rescaling
The script continues with the exploration of the effective potential in a central potential problem. The professor introduces a rescaling of the wave function to eliminate the radial dependence in the equation, leading to a cleaner one-dimensional energy eigenvalue equation. The effective potential is shown to consist of the original potential plus a term related to the angular momentum, which becomes significant near the origin and falls off rapidly with distance.
🔬 Angular Momentum Barrier and Quantum Stability
The professor discusses the concept of the angular momentum barrier, which arises from the kinetic energy associated with angular momentum. As particles approach the origin, their angular velocity and thus kinetic energy increase, creating a potential barrier. However, this barrier does not prevent decay in quantum systems like hydrogen, which remains stable due to other quantum mechanical effects.
🔍 Boundary Conditions and Energy Degeneracy
The script addresses the boundary conditions for wave functions in central potentials, emphasizing that the wave function must vanish at the origin to avoid unphysical energy divergences. The professor also explains the degeneracy of energy levels with respect to the magnetic quantum number m, which is a consequence of rotational symmetry. The energy levels depend on the total angular momentum quantum number l but not on m, leading to 2l+1-fold degeneracy for each energy level.
🌀 Spherical Well Potential and Its Solutions
The professor presents a simplified model of a spherical well potential to illustrate the application of the concepts discussed. By considering the special case of zero angular momentum, the professor derives the wave function and energy levels for the system. The solutions are found to satisfy boundary conditions at the origin and at the well's edge, leading to quantized energy levels. The wave functions are expressed in terms of spherical harmonics and a radial function, which is a sine function of the product of the angular frequency and the radial distance.
🚀 Toy Model for Hydrogen and Coulomb Potential
The script concludes with an introduction to the toy model for the hydrogen atom, which is an idealized version of the Coulomb potential. The professor emphasizes that this model, while not exact, provides a good first approximation to the behavior of hydrogen. The potential is derived from the assumption of point particles with specific charges and masses, leading to a simple inverse-square law. The professor also introduces the characteristic length and energy scales for the system, setting the stage for a more detailed analysis in subsequent lectures.
🔬 Dimensional Analysis and Series Expansion for Coulomb Potential
The professor applies dimensional analysis to the Coulomb potential problem, introducing a characteristic length scale and energy for the system. The script then outlines the method for solving the resulting differential equation, which involves asymptotic analysis and a series expansion. The solutions are expressed in terms of dimensionless variables, and the energy levels are related to integer quantum numbers. The professor also discusses the implications of the solutions for the observed spectrum of hydrogen, highlighting the agreement with the Rydberg formula and the unexpected degeneracy of energy levels.
Mindmap
Keywords
💡Angular Momentum
💡Stern Gerlach Experiment
💡Commutation Relations
💡Wave Function
💡Quantum Mechanics
💡Central Potential
💡Spherical Coordinates
💡Laplacian Operator
💡Hydrogen Atom
💡Spherical Harmonics
💡Separation of Variables
Highlights
Introduction to the concept of angular momentum and its significance in quantum mechanics.
Discussion on the commutation relations of angular momentum operators and their implications.
Explanation of the peculiar nature of half-integer spin states and their inability to be represented as a probability distribution on a sphere.
Preview of the Stern-Gerlach experiment and its role in revealing the quantized nature of angular momentum.
Introduction to the concept of magnetic moment and its relation to angular momentum.
Explanation of how the Stern-Gerlach experiment measures the angular momentum of electrons by observing their deflection in a magnetic field gradient.
Discussion on the intrinsic angular momentum of electrons, known as spin, and its distinction from classical rotational angular momentum.
Introduction to spherical coordinates and the Laplacian operator in three dimensions.
Explanation of the energy operator for systems with central potentials and its simplification through separation of variables.
Derivation of the radial part of the Schrödinger equation for central potentials and its resemblance to a one-dimensional problem.
Introduction to the concept of effective potential in the context of central potentials and its significance.
Discussion on the boundary conditions for wave functions at the origin in central potential problems.
Explanation of the angular momentum barrier and its implications for the behavior of wave functions near the origin.
Introduction to the spherical well potential as a model problem for central potentials.
Solution of the spherical well potential for the special case of zero angular momentum and its implications.
Discussion on the general properties of central potentials, including the independence of energy on the magnetic quantum number m.
Introduction to the Coulomb potential as a central potential and its relevance to the hydrogen atom model.
Construction of a toy model for the hydrogen atom using the Coulomb potential and its limitations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: