Physics - Optics: Lenses (1 of 2) Diverging Lens

Michel van Biezen
30 Apr 201304:29
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores the concept of a diverging lens, a unique optical element that causes parallel light rays to spread out as if emanating from a focal point in front of the lens. The presenter demonstrates how to determine the position and characteristics of the virtual image formed by a diverging lens using geometric techniques and equations. They calculate the image location and magnification for an object placed beyond the lens's focal point, revealing a smaller, upright virtual image. The script also hints at further exploration with objects placed inside the focal point in a subsequent video.

Takeaways
  • 🌟 The video discusses a new type of lens called the diverging lens, which is unique in its properties compared to other lenses.
  • 🔍 When light rays parallel to the normal pass through a diverging lens, they diverge as if emanating from a focal point in front of the lens.
  • 📐 The name 'diverging lens' comes from the way it causes light rays to spread outward from the focal point, unlike converging lenses that bring rays together.
  • 👀 For the first example, an object is placed beyond the focal point of the lens, and the video explains how to determine the location of the image formed.
  • 📏 The technique involves drawing rays from the object, one parallel to the normal and the other through the focal point, to predict where the image will form.
  • ✏️ The video uses a blue pen to illustrate the path of the rays and how they diverge after passing through the lens.
  • 🧠 The human brain interprets the diverging rays as if they were coming from a single point, creating a virtual image on the opposite side of the lens.
  • 🔢 The exact location of the image is calculated using the lens equation \( S' = \frac{S \times F}{S - F} \), where \( S \) is the object distance, \( F \) is the focal length, and \( S' \) is the image distance.
  • 📉 In the example, with an object at 50 cm and a focal length of -25 cm, the calculation shows the image forms at -16.7 cm, indicating a virtual image in front of the lens.
  • 🔄 The magnification of the image is determined to be 1/3 of the object's size, and since it's positive, the image is upright and has the same orientation as the object.
  • 🔄 The video also hints at trying another example with the object placed inside the focal point to explore how it affects the image formation with a diverging lens.
Q & A

  • What is a diverging lens?

    -A diverging lens is a type of lens that causes light rays to spread out or diverge. Unlike converging lenses, which bring light rays together, diverging lenses cause the rays to appear as if they are coming from a focal point in front of the lens.

  • How do light rays behave when they pass through a diverging lens?

    -When light rays parallel to the normal enter a diverging lens, they diverge as if they originated from a focal point in front of the lens. This causes the rays to spread out rather than converging at a point.

  • What is the significance of the focal point in the context of a diverging lens?

    -For a diverging lens, the focal point is significant because it is the point from which the diverging rays appear to originate. Since the lens is diverging, the focal length is negative, and the focal point is located in front of the lens.

  • How does the position of an object relative to the focal point of a diverging lens affect the image formation?

    -The position of the object relative to the focal point of a diverging lens determines where the image will appear and its characteristics. If the object is beyond the focal point, the image will be formed on the same side of the lens as the object, but it will be virtual and smaller in size.

  • What is the equation used to determine the image distance (S') in the context of a diverging lens?

    -The equation used to determine the image distance (S') for a lens is S' = S * F / (S - F), where S is the distance to the object, and F is the focal length. For a diverging lens, the focal length (F) is negative.

  • What does a negative focal length indicate for a lens?

    -A negative focal length indicates that the lens is a diverging lens. This means that it causes light rays to spread out rather than converging at a point, which is characteristic of a converging lens.

  • How can you determine the exact location of the image formed by a diverging lens?

    -You can determine the exact location of the image by using the lens equation S' = S * F / (S - F) and plugging in the known values for the object distance (S) and the focal length (F) of the lens.

  • What is the difference between a real image and a virtual image in the context of lens optics?

    -A real image is formed where light rays actually converge and can be projected onto a screen, whereas a virtual image is formed where the light rays appear to diverge from. A virtual image cannot be projected onto a screen but can be seen by looking into the lens.

  • What does the magnification (m) of an image indicate?

    -The magnification (m) of an image indicates how much larger or smaller the image is compared to the object. It is calculated as the ratio of the image distance (S') to the object distance (S). A positive magnification means the image is upright, while a negative magnification would mean the image is inverted.

  • How does the orientation of the image relate to the magnification value in the context of a diverging lens?

    -If the magnification value is positive, it indicates that the image is upright and in the same orientation as the object. If it were negative, the image would be inverted, which is not the case with a diverging lens as described in the script.

  • What happens when an object is placed inside the focal point of a diverging lens?

    -When an object is placed inside the focal point of a diverging lens, the image will still be virtual and appear on the same side of the lens as the object. However, the exact location and size of the image will differ from when the object is placed beyond the focal point.

Outlines
00:00
🔎 Introduction to Diverging Lenses

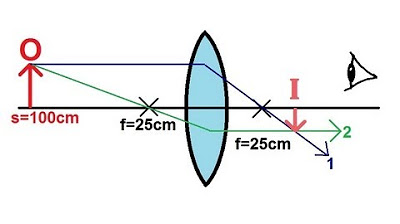
This paragraph introduces the concept of a diverging lens, a type of lens that causes light rays to spread apart. It explains that unlike converging lenses, diverging lenses have a negative focal length and that rays parallel to the normal appear to come from a focal point in front of the lens. The explanation includes a step-by-step guide on how to trace rays through a lens to determine the location of the virtual image formed by the lens. The presenter uses a blue pen to illustrate the process and mentions the use of specific techniques and equations to calculate the image location.

📏 Calculating Image Location with Diverging Lens

The second paragraph delves into the practical application of the principles discussed in the first paragraph. It describes a scenario where an object is placed beyond the focal point of a diverging lens and uses the lens formula \( S' = \frac{S \times F}{S - F} \) to calculate the exact location of the image formed. The presenter provides numerical values, with the object distance (S) being 50 cm and the focal length (F) being -25 cm, leading to a calculation that results in an image distance (S') of -16.7 cm, indicating a virtual image located 16.7 cm in front of the lens. The paragraph also explains the concept of magnification (m), calculating it to be 1/3, which means the image is one-third the size of the object and is upright.

Mindmap
Keywords
💡Diverging Lens
A diverging lens is an optical component that spreads out light rays that pass through it. In the context of the video, it is a type of lens that causes parallel light rays to diverge as if they originated from a focal point in front of the lens. This concept is central to the video's theme of exploring how different types of lenses affect light paths.
💡Focal Point
The focal point is the point where parallel rays of light converge after passing through a converging lens, or appear to diverge from in the case of a diverging lens. In the video, the focal point is used to describe the apparent origin of the diverging light rays, which is crucial for understanding how the lens forms images.
💡Normal
In optics, the normal is an imaginary line perpendicular to the surface of a lens at a particular point. The script refers to rays being parallel to the normal, indicating that they are entering the lens at a right angle to the lens surface, which is a standard condition for lens behavior analysis.
💡Ray Tracing
Ray tracing is a method used to predict the path of light through an optical system by drawing representative rays and observing their behavior after interacting with lenses or mirrors. The video uses ray tracing to demonstrate how rays behave when passing through a diverging lens.
💡Virtual Image
A virtual image is an image that appears to be located at a point from which light does not actually come; it cannot be projected onto a screen. The video explains that the image formed by a diverging lens is virtual because it is located in front of the lens and is a result of the brain interpreting the diverging rays.
💡Focal Length
Focal length is a measure of a lens's ability to bend light, defined as the distance from the lens to the focal point. In the video, the focal length of a diverging lens is negative, indicating that its focal point is on the same side as the incoming light, which is essential for understanding the lens's effect on light rays.
💡Magnification
Magnification is the ratio of the image size to the object size, indicating how much larger or smaller the image appears compared to the object. The video calculates the magnification of the image formed by the diverging lens, showing that it is one-third the size of the object, which is a key aspect of the lens's imaging properties.
💡Upright Image
An upright image is one that maintains the same orientation as the original object. The video mentions that the image formed by the diverging lens is upright, which means it is not inverted, and this is an important characteristic of the image's appearance.
💡Lens Equation
The lens equation relates the object distance, image distance, and focal length to describe the behavior of lenses. The video uses the lens equation (S' = S * F / (S - F)) to calculate the image distance for a diverging lens, which is a fundamental concept in lens optics.
💡Negative Sign
In the context of the video, a negative sign indicates the direction or position relative to the lens. For example, a negative focal length indicates a diverging lens, and a negative image distance indicates that the image is in front of the lens, forming a virtual image.
Highlights

Introduction to the concept of a diverging lens, which is a unique type of lens that causes light rays to diverge as if they originated from a focal point in front of the lens.

Explanation of how a diverging lens works with parallel light rays in relation to the normal, resulting in the rays appearing to come from a virtual focal point.

Demonstration of the path a ray of light takes through a diverging lens, using a drawing to illustrate the concept.

Description of the process to determine the location of the image formed by a diverging lens when an object is placed beyond the lens's focal point.

Use of specific techniques with a blue pen to illustrate the path of light rays and the formation of the image.

Detailed explanation of the first ray's behavior when it diverges from the lens as if coming from the focal point in front of the lens.

Clarification on the negative focal length of a diverging lens and its implications on the location of the focal point.

The observer's perception of the diverging rays and the brain's interpretation to form a virtual image.

Calculation of the exact location of the image using the lens equation and substitution of given values.

Result of the calculation indicating the image distance and its negative value signifying a virtual image.

Explanation of the virtual image's position in front of the lens and its relation to the focal point.

Introduction to the concept of magnification and its calculation for a diverging lens.

Determination of the image's size as one-third of the object's size and its upright orientation.

Conclusion on how the image is formed with a diverging lens and its characteristics.

Announcement of a follow-up example involving an object placed inside the focal point of a diverging lens in the next video.

Transcripts

Browse More Related Video

Physics - Optics: Lenses (2 of 2) Diverging Lens

Physics - Optics: Lenses (3 of 4) Converging Lens

GCSE Physics - How to Draw Ray Diagrams #70

Multiple Two Lens System with Diverging and Converging Lens

Physics - Optics: Lenses (3 of 5) Lens Combinations - Converging & Diverging Lenses

Physics - Optics: Lenses (1 of 4) Converging Lens

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
OpticsPhysicsDiverging LensesVirtual ImageThin LensesLight RaysFocal PointLens CalculationsRay DiagramsEducation