Physics 52 Refraction and Snell's Law (3 of 11) Light Ray Through A Prism

Michel van Biezen
29 Apr 201308:01
EducationalLearning
32 Likes 10 Comments

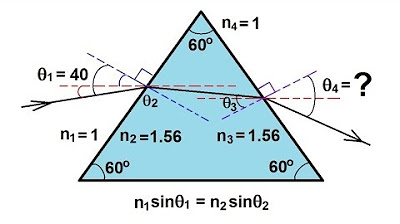
TLDRThis educational script demonstrates the concept of refraction across two boundaries using a block of glass with an index of refraction 1.5. It explains how light bends when moving from a lower to a higher index of refraction and vice versa. The process involves identifying angles of incidence and refraction at each boundary, applying Snell's law to calculate unknown angles, and using geometric relationships to deduce the final angle of refraction, theta sub 4, which is found to be 25.6 degrees.

Takeaways
  • 🌟 Refraction occurs when light passes through different media with varying indices of refraction.
  • 🔍 The index of refraction for glass in the example is 1.5.
  • 📐 Snell's Law is used to calculate the angles of refraction at each boundary.
  • 📏 Angle of incidence is labeled as θ1, and the first angle of refraction is θ2.
  • 🎯 The angle of incidence on the second boundary is θ3, and the final angle of refraction is θ4.
  • 📚 The indices of refraction on each side of the boundaries are denoted as n1, n2, n3, and n4.
  • 🔄 When light travels from a lower to a higher index of refraction, it bends towards the normal.
  • 🔄 Conversely, when light travels from a higher to a lower index of refraction, it bends away from the normal.
  • 📐 To find θ1, the script uses the geometry of the setup and alternate interior angles.
  • 🧭 θ2 is calculated using Snell's Law rearranged to solve for the sine of θ2.
  • 📐 θ3 is determined by the geometry of the light path and the angles formed within the glass block.
  • 🔢 θ4 is found by applying Snell's Law again, using the known values of θ3 and the indices of refraction.
  • 📝 The importance of correct notation from the beginning is emphasized for ease of calculation.
Q & A

  • What is the index of refraction of the glass block described in the script?

    -The index of refraction of the glass block is 1.5.

  • What is the phenomenon where light bends when it passes from one medium to another?

    -The phenomenon is called refraction.

  • Why does the beam of light bend or refract when it passes from a low to a high index of refraction?

    -The beam bends or refracts towards the normal because the speed of light decreases in the higher index medium, changing its direction.

  • How does the script determine the initial angle of incidence (theta sub 1)?

    -The script uses the fact that the incoming ray is parallel to the boundary and the normal to the boundary forms a right angle with the ray, concluding that theta sub 1 is 45 degrees.

  • What is Snell's law and how is it applied in the script?

    -Snell's law states that n1 * sin(theta1) = n2 * sin(theta2), where n1 and n2 are the indices of refraction and theta1 and theta2 are the angles of incidence and refraction, respectively. It is applied to find the angles of refraction when the angles of incidence and indices of refraction are known.

  • How is the angle of refraction across the first boundary (theta sub 2) calculated?

    -Theta sub 2 is calculated using Snell's law by rearranging the formula to solve for sin(theta2) and then taking the arcsine (inverse sine) of the result.

  • What is meant by 'alternate interior angles' in the context of the script?

    -Alternate interior angles are angles that are on opposite sides of a transversal cutting across two parallel lines, and they are equal in measure.

  • How is theta sub 3 determined in the script?

    -Theta sub 3 is determined by understanding that it is equal to the angle formed by the light beam and the boundary after refraction through the first boundary, which is calculated as 45 degrees minus theta sub 2.

  • What is the final step to find theta sub 4 using the information from the script?

    -The final step is to apply Snell's law again with the known values of theta sub 3, n3 (index of refraction inside the glass), and n4 (index of refraction in air), and then calculate theta sub 4 using the arcsine function.

  • What is the final calculated value for theta sub 4 in the script?

    -The final calculated value for theta sub 4 is 25.6 degrees.

  • Why is it important to keep track of notations when solving refraction problems as described in the script?

    -Keeping track of notations is important to ensure that the correct values are used in the equations, which simplifies the process of solving the problem and avoids errors.

Outlines
00:00
🔍 Understanding Refraction Across Two Boundaries

This paragraph explains the process of refraction through a block of glass with an index of refraction of 1.5. It describes how light travels through two boundaries, starting from an initial angle of incidence, θ1, refracting at the first boundary to angle θ2, and then at the second boundary to angle θ4. The importance of identifying these angles correctly is emphasized, using Snell's Law to calculate θ2 and θ4. Key steps include recognizing alternate interior angles and applying trigonometric principles to find the angles at each boundary.

05:00
📐 Applying Snell's Law to Find Refraction Angles

This paragraph continues the explanation by calculating θ3 and θ4 using Snell's Law. It highlights the process of determining θ3 by understanding that it is the complement of the sum of θ2 and a known angle of 45 degrees. After finding θ3, Snell's Law is applied again to determine θ4, which involves taking the inverse sine of the product of refractive indices and the sine of θ3. The final answer for θ4 is obtained, demonstrating the systematic approach to solving the problem.

Mindmap
Keywords
💡Refraction
Refraction is the bending of light as it passes from one medium to another with a different refractive index. In the video, refraction is the central phenomenon being discussed, with the light ray bending as it moves from air to glass and then back to air. The script uses refraction to explain the behavior of light at different boundaries, demonstrating how the angle of incidence and the refractive indices of the media determine the bending of the light ray.
💡Index of Refraction
The index of refraction is a measure of how much light slows down and bends when it enters a medium from a vacuum or from another medium. In the script, the index of refraction is given as 1.5 for the glass block, which is a key factor in calculating the angles of refraction at the boundaries. The index of refraction is used to apply Snell's law, which is central to solving the problem presented in the video.
💡Snell's Law
Snell's Law, also known as the law of refraction, relates the angles of incidence and refraction to the refractive indices of the two media. In the video, Snell's Law is used to calculate the unknown angles of refraction at the glass boundaries. The script demonstrates how to rearrange the formula to solve for the unknown angle, using the known angles and refractive indices.
💡Angle of Incidence
The angle of incidence is the angle at which a wave approaches a boundary or interface. In the context of the video, the angle of incidence is used to describe the initial angle at which the light ray strikes the first boundary of the glass block. The script mentions specific angles of incidence, such as 'theta of 1' and 'theta of 3', which are essential for applying Snell's Law.
💡Angle of Refraction
The angle of refraction is the angle at which a wave is refracted when it passes into a medium with a different refractive index. The video script describes how to calculate the angle of refraction across the first and second boundaries using the given angles of incidence and the refractive indices of the media involved.
💡Numerix
Numerix, likely a typographical error in the script for 'numerical', refers to the numerical values used in the calculations. The script uses numerix values such as the refractive index of 1.5 for glass and the angles of incidence and refraction to demonstrate the calculations involved in solving the refraction problem.
💡Alternate Interior Angles
Alternate interior angles are a pair of angles that are on opposite sides of a transversal cutting across two parallel lines. In the script, the concept of alternate interior angles is used to deduce the value of theta sub 1 as 45 degrees, based on the given information about the angles in the diagram.
💡Normal
The normal is a line perpendicular to the surface at the point of incidence or refraction. The script mentions the normal in the context of drawing the light ray's path and in calculating the angles of incidence and refraction, which are measured with respect to the normal.
💡Arcsine
Arcsine, or inverse sine, is a trigonometric function that returns the angle whose sine is a given number. In the video, arcsine is used to calculate the angles of refraction after determining the sine values using Snell's Law and the refractive indices.
💡Light Ray
A light ray is a simplified representation of the path that light takes. In the script, the light ray is used to illustrate the process of refraction as it enters and exits the glass block, demonstrating how the ray bends at the boundaries due to the change in refractive index.
💡Boundary
A boundary in this context refers to the interface between two different media, such as air and glass. The script discusses refraction across two boundaries, explaining how the light ray behaves as it passes from one medium to another, and how the refractive indices and angles of incidence affect this behavior.
Highlights

Introduction to refraction across two boundaries with a block of glass.

Explanation of index of refraction and its importance in the refraction process.

Demonstration of how the angle of incidence and refraction are related in the first boundary.

Use of Snell's law to calculate the angle of refraction across the first boundary.

Calculation of theta sub 2 using the inverse sine function and given values.

Illustration of alternate interior angles to determine theta sub 1 as 45 degrees.

Derivation of theta sub 3 by understanding the geometry of the light path and angles.

Calculation of theta sub 3 using the difference between known angles.

Application of Snell's law again to find theta sub 4 after determining theta sub 3.

Final calculation of theta sub 4 using the arcsine function with the derived values.

Emphasis on the importance of correct notations for easier calculations.

Explanation of the refraction process from high to low index of refraction and vice versa.

Visual representation of how light bends when transitioning between different media.

The significance of understanding the normal in the context of refraction.

Step-by-step guide on how to approach the problem of refraction across two boundaries.

The challenge of finding all the angles involved in the refraction process.

Recap of the process to find theta sub 1, 2, 3, and 4 in the context of refraction.

Practical application of geometric principles in solving refraction problems.

Transcripts

Browse More Related Video

Snell's Law & Index of Refraction Practice Problems - Physics

Total Internal Reflection of Light and Critical Angle of Refraction Physics

Refraction of Light

Physics 52 Refraction and Snell's Law (9 of 11) Ex. 4: Light Through a Prism

Refraction and Snell's law | Geometric optics | Physics | Khan Academy

Refraction of Light

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
RefractionSnell's LawPhysicsOpticsEducationalGlass BlockIndex of RefractionLight BeamAngle CalculationScience Tutorial