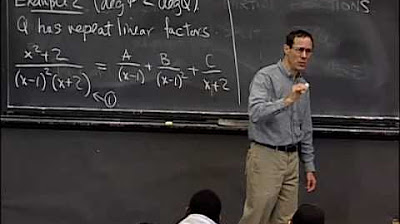Unit VI: Lec 2 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis MIT OpenCourseWare video introduces the technique of partial fractions, a powerful method for integrating rational functions where the numerator's degree is less than the denominator's. The professor explains the process of breaking down complex integrands into simpler linear and quadratic fractions, solving for unknown coefficients, and integrating them. The lesson also touches on the application of partial fractions to integrals involving trigonometric functions, showcasing the method's versatility in simplifying complex mathematical problems.
Takeaways
- 📚 The script introduces the technique of partial fractions, a method for integrating rational functions where the numerator is of a lesser degree than the denominator.
- 🔑 It is emphasized that partial fractions are particularly useful for integrals involving the quotient of two polynomials, and the degree of the numerator must be less than the degree of the denominator.
- 📐 The professor discusses the theoretical possibility of factoring every real polynomial into linear and quadratic terms, but acknowledges the practical difficulty of finding such factorizations.
- 📉 The script covers the concept of using trigonometric identities and substitutions to transform integrals involving sine and cosine into a form that can be handled by partial fractions.
- 🧩 The technique of undetermined coefficients is introduced, where unknown constants are assumed in the partial fraction decomposition, and then determined by equating coefficients.
- 🔍 The process of equating coefficients from the identity formed by partial fraction decomposition is used to solve for the unknown constants in the numerators.
- 📝 The script provides an example of how to apply partial fractions to a specific integral involving a linear and a quadratic polynomial in the denominator.
- 📉 The professor explains how to differentiate the result of an integral to verify its correctness by obtaining the original integrand.
- 🤔 The script warns about the potential pitfalls of assuming that equal expressions with different terms allow for equating coefficients directly, highlighting the importance of mathematical rigor.
- 📈 An example is given to illustrate the use of partial fractions in integrating functions involving trigonometric expressions by substitution.
- 🔑 The script concludes by mentioning that partial fractions is not only a standalone technique but also a gateway to integrating more complex functions involving trigonometric polynomials.
Q & A
What is the technique of partial fractions?
-The technique of partial fractions is a method used in calculus to integrate rational functions, particularly when the integral has the form of the quotient of two polynomials, where the degree of the numerator is less than the degree of the denominator.
Why is it assumed that the degree of P is less than the degree of Q in partial fraction decomposition?
-This assumption is made because it simplifies the integration process. If the degree of P is not less than Q, long division is performed first to simplify the expression into a form where this condition is met, making it easier to apply the technique of partial fractions.
What is the significance of the statement that every real polynomial can be factored into linear and quadratic terms?
-This statement is significant because it underpins the partial fractions technique, which relies on the ability to express the denominator of a rational function as a product of linear and quadratic factors, allowing for easier integration.
Why is it mentioned that not all polynomials can be factored into real numbers?
-Some polynomials, especially those with a degree greater than 2, may not have real roots and thus cannot be factored into real linear and quadratic terms. In such cases, complex numbers may be introduced, as exemplified by the factorization of x^2 + 1 into (x + i)(x - i).
What is the method of undetermined coefficients?
-The method of undetermined coefficients is a technique used to find the particular form of a solution to a differential equation or, in the context of partial fractions, to determine the unknown constants in the decomposed fractions.
How does the professor illustrate the process of partial fraction decomposition?
-The professor illustrates the process by decomposing the integral of 1/[(x - 1)(x^2 + 1)] into simpler fractions with linear and quadratic denominators and then determining the unknown coefficients by equating the numerators after setting the expressions equal to each other.
What is the importance of polynomial identities in the context of partial fractions?
-Polynomial identities are crucial because they allow for the equating of coefficients of corresponding terms on both sides of an identity, which is a key step in solving for the unknown coefficients in partial fraction decomposition.
Why is it emphasized that the technique of partial fractions works for the quotient of two polynomials?
-It is emphasized because the method is specifically tailored for integrals of rational functions where the degree of the polynomial in the numerator is less than that in the denominator, making it a powerful tool for integrating such functions.
What is the role of differentiation in verifying the result obtained from partial fraction decomposition?
-Differentiation is used to verify the result by showing that the integrated function, when differentiated, yields the original integrand, thus confirming the correctness of the integration process.
How does the script mention the application of partial fractions to integrals involving trigonometric functions?
-The script suggests that partial fractions can be applied to integrals involving trigonometric functions by making suitable substitutions, such as setting z equal to the tangent of x/2, which transforms the trigonometric functions into polynomial quotients in terms of z.
Outlines
📚 Introduction to Partial Fractions Technique
The script begins with a female voice introducing the video content under a Creative Commons license and urging support for MIT OpenCourseWare. A professor then dives into the topic of partial fractions, a technique for integrating rational functions where the degree of the numerator is less than the denominator. The importance of factoring polynomials into linear and quadratic terms is emphasized, and the limitations of factoring higher-degree polynomials are discussed, including the introduction of complex numbers for certain quadratic factors. The professor illustrates the method with an example, highlighting the process of breaking down a complex integrand into simpler, integrable fractions.
🔍 Detailed Explanation of Partial Fractions Decomposition
This paragraph continues the discussion on partial fractions, focusing on the decomposition of a complex integrand into simpler fractions with linear and quadratic denominators. The professor uses the example of integrating 1/(x-1)(x^2+1) to demonstrate the method of undetermined coefficients, where unknown constants are solved by equating coefficients from both sides of an identity. The process involves setting up a common denominator and creating a system of equations to solve for the unknowns, ultimately simplifying the integral into more manageable parts.
📈 Polynomial Identities and Their Application in Integration
The script segment discusses the properties of polynomial identities and their application in integration techniques. It emphasizes the importance of matching coefficients when dealing with identical polynomial expressions, and the professor uses the method of undetermined coefficients to find the values of A, B, and C in the context of partial fractions. The summary also includes a cautionary note about the misuse of this technique outside of polynomial identities, highlighting the difference between identities and equations, and the potential pitfalls of assuming coefficient equality without basis.
🧭 The Role of Identities in Reducing Complex Integrands
This paragraph explores the use of trigonometric identities to simplify the integration of functions involving sine and cosine. The professor introduces a substitution method where z equals the tangent of x/2, transforming the integral of secant(x) dx into a form that can be handled with partial fractions. The explanation includes converting dx and trigonometric functions into expressions involving z, and then using partial fractions to integrate the simplified form. The summary underscores the power of reducing complex integrands to familiar forms through creative substitutions and identity applications.
🔑 Unlocking the Integration of Secant(x) Using Substitutions
The script concludes with a specific application of the techniques discussed: integrating secant(x) dx. The professor demonstrates how to use the previously introduced substitution z = tan(x/2) to transform the integral into a form involving the quotient of two polynomials in z. This allows for the application of partial fractions to solve the integral in terms of z, which can then be translated back into terms of x. The summary highlights the process of substitution and the importance of recognizing when a complex integral can be simplified through strategic mathematical manipulation.
Mindmap
Keywords
💡Partial Fractions
💡Polynomials
💡Integrating
💡Denominator
💡Numerator
💡Factoring
💡Quotient
💡Unidentified Coefficients
💡Integration by Parts
💡Trigonometric Functions
💡Differentiation
Highlights
Introduction to the technique of partial fractions for integrating the quotient of two polynomials.
Assumption that the degree of the polynomial in the numerator is less than the degree of the polynomial in the denominator for the application of partial fractions.
Explanation of handling integrals with polynomials where the degree of the numerator is greater than the denominator by performing long division first.
Overview of the two key steps in the method of partial fractions: handling denominators involving linear and quadratic polynomials and the theoretical factorization of any real polynomial.
Clarification on the limitations of factoring polynomials into real numbers, especially for quadratic polynomials that may result in non-real roots.
Illustration of the method of partial fractions with the integral of 1 over the product of (x - 1) and (x^2 + 1).
Use of undetermined coefficients to set up the partial fraction decomposition and the resulting system of equations to solve for the coefficients.
Demonstration of solving the system of equations to find the values of the constants A, B, and C in the partial fraction decomposition.
Integration of the original integrand after applying partial fractions and breaking it down into simpler integrals.
Application of trigonometric identities and substitution to express dx, sin(x), and cos(x) as quotients of polynomials in a new variable z.
Transformation of the integral of secant(x) using the substitution z = tan(x/2) and expressing it as an integral in terms of z.
Reduction of the integral of secant(x) to a form that can be solved using partial fractions in the new variable z.
Emphasis on the importance of mathematical rigor when using the technique of partial fractions and the uniqueness of polynomial identities.
Discussion on the concept of linear dependence and independence and its relation to the method of partial fractions.
Introduction of a powerful technique more general than partial fractions, to be discussed in the next lesson.
Acknowledgment of the Gabriella and Paul Rosenbaum Foundation for funding the publication of the video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: